Articles by tag: Properties

LTL Tutor
Differential Analysis: A Summary
Forge: A Tool to Teach Formal Methods
Generating Programs Trivially: Student Use of Large Language Models
Automated, Targeted Testing of Property-Based Testing Predicates
Teaching and Assessing Property-Based Testing


LTL Tutor

Tags: Linear Temporal Logic, Education, Formal Methods, Misconceptions, Properties, Tools, Verification

Posted on 08 August 2024.

We have been engaged in a multi-year project to improve education in Linear Temporal Logic (LTL) [Blog Post 1, Blog Post 2]. In particular, we have arrived at a detailed understanding of typical misconceptions that learners and even experts have. Our useful outcome from our studies is a set of instruments (think “quizzes”) that instructors can deploy in their classes to understand how well their students understand the logic and what weaknesses they have.

However, as educators, we recognize that it isn’t always easy to add new materials to classes. Furthermore, your students make certain mistakes—now what? They need explanations of what went wrong, need additional drill problems, and need checks whether they got the additional ones right. It’s hard for an educator to make time for all that. And if one is an independent learner, they don’t even have access to such educators.

Recognizing these practical difficulties, we have distilled our group’s expertise in LTL into a free online tutor:

https://ltl-tutor.xyz

We have leveraged insights from our studies to create a tool designed to be used by learners with minimal prior instruction. All you need is a brief introduction to LTL (or even just propositional logic) to get started. As an instructor, you can deliver your usual lecture on the topic (using your preferred framing), and then have your students use the tool to grow and to reinforce their learning.

In contrast to traditional tutoring systems, which are often tied to a specific curriculum or course, our tutor adaptively generates multiple-choice question-sets in the context of common LTL misconceptions.

  • The tutor provides students who get a question wrong with feedback in terms of their answer’s relationship to the correct answer. Feedback can take the form of visual metaphors, counterexamples, or an interactive trace-stepper that shows the evaluation of an LTL formula across time.
In this example of LTL tutor feedback, a diagram is used to show students that their answer is logically more permissive than the correct answer to the question. The learner is also shown an example of an LTL trace that satisfies their answer but not the correct answer.
In this example of LTL tutor feedback, a diagram is used to show students that their answer is logically more permissive than the correct answer to the question. The learner is also shown an example of an LTL trace that satisfies their answer but not the correct answer.
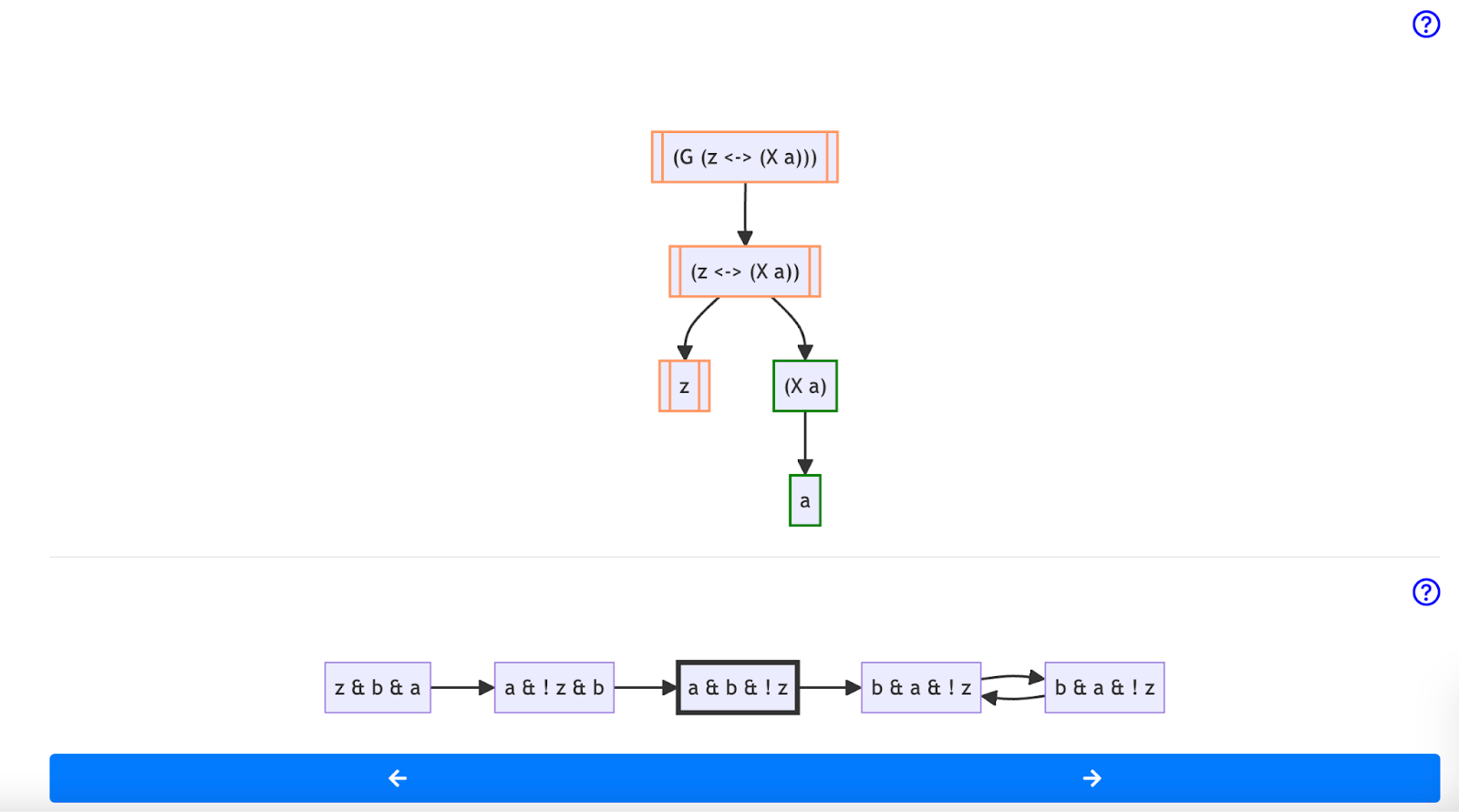
In this example of interactive stepper usage, the user examines the satisfaction of the formula (G (z <-> X(a))) in the third state of a trace. While the overall formula is not satisfied at this moment in time, the sub-formula (X a) is satisfied. This allows learners to explore where their understanding of a formula may have diverged from the correct answer.
In this example of interactive stepper usage, the user examines the satisfaction of the formula (G (z <-> X(a))) in the third state of a trace. While the overall formula is not satisfied at this moment in time, the sub-formula (X a) is satisfied. This allows learners to explore where their understanding of a formula may have diverged from the correct answer.
  • If learners consistently demonstrate the same misconception, the tutor provides them further insight in the form of tailored text grounded in our previous research.
Here, a student who consistently assumes the presence of the `Globally` operator even when it is not present, is given further insight into the pertinent semantics of the operator.
Here, a student who consistently assumes the presence of the `Globally` operator even when it is not present, is given further insight into the pertinent semantics of the operator.
  • Once it has a history of misconceptions exhibited by the student, the tutor generates novel, personalized question sets designed to drill students on their specific weaknesses. As students use the tutor, the system updates its understanding of their evolving needs, generating question sets to address newly uncovered or pertinent areas of difficulty.

We also designed the LTL Tutor with practical instructor needs in mind:

  • Curriculum Agnostic: The LTL Tutor is flexible and not tied to any specific curriculum. You can seamlessly integrate it into your existing course without making significant changes. It both generates exercises for students and allows you to import your own problem sets.
  • Detailed Reporting: To track your class’s progress effectively, you can create a unique course code for your students to enter, so you can get detailed insights into their performance.
  • Self-Hostable: If you prefer to have full control over your data, the LTL Tutor can easily be self-hosted.

To learn more about the Tutor, please read our paper!

Differential Analysis: A Summary

Tags: Differential Analysis, Formal Methods, Properties, Verification

Posted on 27 June 2024.

For multiple decades we have worked on a the problem of differential analysis. This post explains where it comes from, what it means, and what its consequences are.

Context: Verification

For decades, numerous researchers have worked on the problem of verification. To a first approximation, we can describe this problem as follows:

P ⊧ ɸ

That is, checking whether some program P satisfies some property ɸ. There have been many productive discussions about exactly what methods we should use, but this remains the fundamental question.

Starting in around 2004, we started to build tools to verify a variety of interesting system descriptions (the Ps), starting with access-control policies. They could also be security policies, network configurations, and more. We especially recognized that many of these system descriptions are (sufficiently) sub-Turing-complete, which means we can apply rich methods to precisely answer questions about them. That is, there is a rich set of problems we can verify.

The Problem

Attractive as this idea is, it runs into a significant problem in practice. When you speak to practitioners, you find that they are not short of system descriptions (Ps), but they are severely lacking in properties (ɸs). The problem is not what some might imagine — that they can’t express their properties in some precise logic (which is a separate problem!) — but rather that they struggle to express non-trivial properties at all. A typical conversation might go like:

  • We have a tool for verification!
  • Nice, what does it do?
  • It consumes system descriptions of the kind you produce!
  • Oh, that’s great!
  • You just need to specify your properties.
  • My what?
  • Your properties! What you want your system to do!
  • I don’t have any properties!
  • But what do you want the system to do?
  • … Work correctly?

This is not to mock practitioners: not at all. Quite the contrary! Even formal methods experts would struggle to precisely describe the expected behavior of complex systems. In fact, talk to formal methods researchers long enough and they’ll admit knowing that this is a problem. It’s just not something we like to think about.

An Alternative

In fact, the “practitioner” answer shows us the path forward. What does it mean for a system to “work”? How does a system’s maintainer know that it “works”?

As a practical matter, many things help us confirm that a system is working well enough. We might have some test suites, we might have monitoring of its execution, we observe it run and use it; lots of people are using it every day; we might even have verified a few properties of a few parts! The net result is that we have confidence in a system.

And then, things happen! Typically, one of two things:

  • We find a bug, and need to fix it.
  • We modify an existing feature or add a new one (or — all too rarely — remove one!).

So the problem we run into is the following:

How do we transfer the confidence we had
in the old version to the new one?

Put differently, the core of formal methods is checking for compatibility between two artifacts. Traditionally, we have a system description (P) and a property (ɸ); these are meant to be expressed independent of one another, so that compatibility gives us confidence and incompatibility indicates an error. But now we have two different artifacts: an old system (call it P) and a new one (call it P’). These are obviously not going to be the same (except in rare cases; see below), but broadly, we want to know, how are they different?

P - P'

Of course, what we care about is not the syntactic difference, but the semantic change. Large syntactic differences may have small semantic ones and vice versa.

Defining the Difference

Computing the semantic difference is often not easy. There is a long line of work of computing the difference of programs. However, it is difficult for Turing-complete languages; it is also not always clear what the type of the difference should be. Computing it is a lot easier when the language is sub-Turing-complete (as our papers show). The question of exactly what a “difference” is is also interesting.

Many of the system description languages we have worked with tend to be of the form Request ⇒ Response. For instance, an access control policy might have the type:

Request ⇒ {Accept, Deny}

(In practice, policy languages can be much richer, but this suffices for illustration.) So what is the type of the difference? It maps every request to the cross-product of responses:

Request ⇒ {Accept↦Accept, Deny↦Deny, Accept↦Deny, Deny↦Accept}

That is: some requests that used to be accepted still are; some that were denied still are; but some that were accepted are now deined, and some that were denied are now accepted. (This assumes the domains are exactly the same; otherwise some requests that previously produced a decision no longer do, and vice versa. We’ll assume you can work out the details of domains with bottom values.) The difference is of course the requests whose outcomes change: in this case,

Request ⇒ {Accept↦Deny, Deny↦Accept}

Using the Difference

Depending on how we compute the difference, we can treat the difference essentially as a database. That is, it is a set of pairs of request and change-of-response. The database perspective is very productive, because we can do many things with this database:

  • Queries: What is the set of requests whose decisions go from Deny↦Accept? These are places where we might look for data leaks.
  • Views: What are all the requests whose decisions go from Accept↦Deny? These are all the requests that lost access. We might then want to perform queries over this smaller database: e.g., who are the entities whose requests fall in it?

And perhaps most surprisingly:

  • Verification: Confirm that as a result of this change, certain entities did not gain access.

In our experience, administrators who would not be able to describe properties of their system can define properties of their changes. Indeed, classical verification even has a name for some such properties: they’re called “frame conditions”, and mean, in effect, “and nothing else changed”. Here, we can actually check for these. It’s worth noting that these properties are not true of either the old or new systems! For instance, certain individuals may have had privileges before and will have them after the alteration; all we’re checking is that their privileges did not change.

Uses

Having a general “semantic difference engine”, and being able to query it (interactively), is very powerful. We can perform all the operations we have described above. We can use it to check the consequences of an intended edit. In some rare cases, we expect the difference to be empty: e.g., when we refactor the policy to clean it up syntactically, but expect that the refactoring had no semantic impact. Finally, a semantic differencing engine is also useful as an oracle when performing mutation testing, as Martin and Xie demonstrated.

A Cognitive Perspective

We think there are a few different, useful framings of differential analysis.

One might sound like a truism: we’re not very good at thinking about the things that we didn’t think about. That is, when we make a change to the system, there was some intent behind the change; but it can be very difficult to determine all the consequences of that change. Our focus on the intended change can easily blind us thinking through the consequences. Overcoming these blind spots is very difficult for humans. A semantic differential analysis engine lays them bare.

Another is that we lack good tools to figure out what the properties of a system should be. Model-exploration tools (such as Alloy, or our derivative of it, Forge) are useful at prompting people to think about how they expect systems to behave and not behave. Differential output can also be such a spur: in articulating why something should or should not happen with a change, we learn more about the system itself.

Finally, it’s worth distinguishing the different conditions that lead to system changes. When working on features, we can often do so with some degree of flexibility. But when fixing bugs, we’re often in a hurry: we need to make a change to immediately block, say, a data leakage. If we’re being principled, we might add some tests to check for the intended behavior (and perhaps also to avoid regression); but at that moment, we are likely to be in an especially poor shape to think through unintended consequences. Differential analysis serves as an aid in preventing fixing one problem introducing another.

Readings

Here are some of our papers describing differential analysis (which we have also called “change-impact analysis” in the past):

Forge: A Tool to Teach Formal Methods

Tags: Education, Formal Methods, Properties, Tools, User Studies, Verification, Visualization

Posted on 21 April 2024.

For the past decade we have been studying how best to get students into formal methods (FM). Our focus is not on the 10% or so of students who will automatically gravitate towards it, but on the “other 90%” who don’t view it as a fundamental part of their existence (or of the universe). In particular, we decided to infuse FM thinking into the students who go off to build systems. Hence the course, Logic for Systems.

The bulk of the course focuses on solver-based formal methods. In particular, we began by using Alloy. Alloy comes with numerous benefits: it feels like a programming language, it can “Run” code like an IDE, it can be used for both verification and state-exploration, it comes with a nice visualizer, and it allows lightweight exploration with gradual refinement.

Unfortunately, over the years we have also run into various issues with Alloy, a full catalog of which is in the paper. In response, we have built a new FM tool called Forge. Forge is distinguished by the following three features:

  1. Rather than plunging students into the full complexity of Alloy’s language, we instead layer it into a series of language levels.

  2. We use the Sterling visualizer by default, which you can think of as a better version of Alloy’s visualizer. But there’s much more! Sterling allows you to craft custom visualizations. We use this to create domain-specific visualizations. As we show in the paper, the default visualization can produce unhelpful, confusing, or even outright misleading images. Custom visualization takes care of these.

  3. In the past, we have explored property-based testing as a way to get students on the road from programming to FM. In turn, we are asking the question, “What does testing look like in this FM setting?” Forge provides preliminary answers, with more to come.

Just to whet your appetite, here is an example of what a default Sterling output looks like (Alloy’s visualizer would produce something similar, with fewer distinct colors, making it arguably even harder to see):

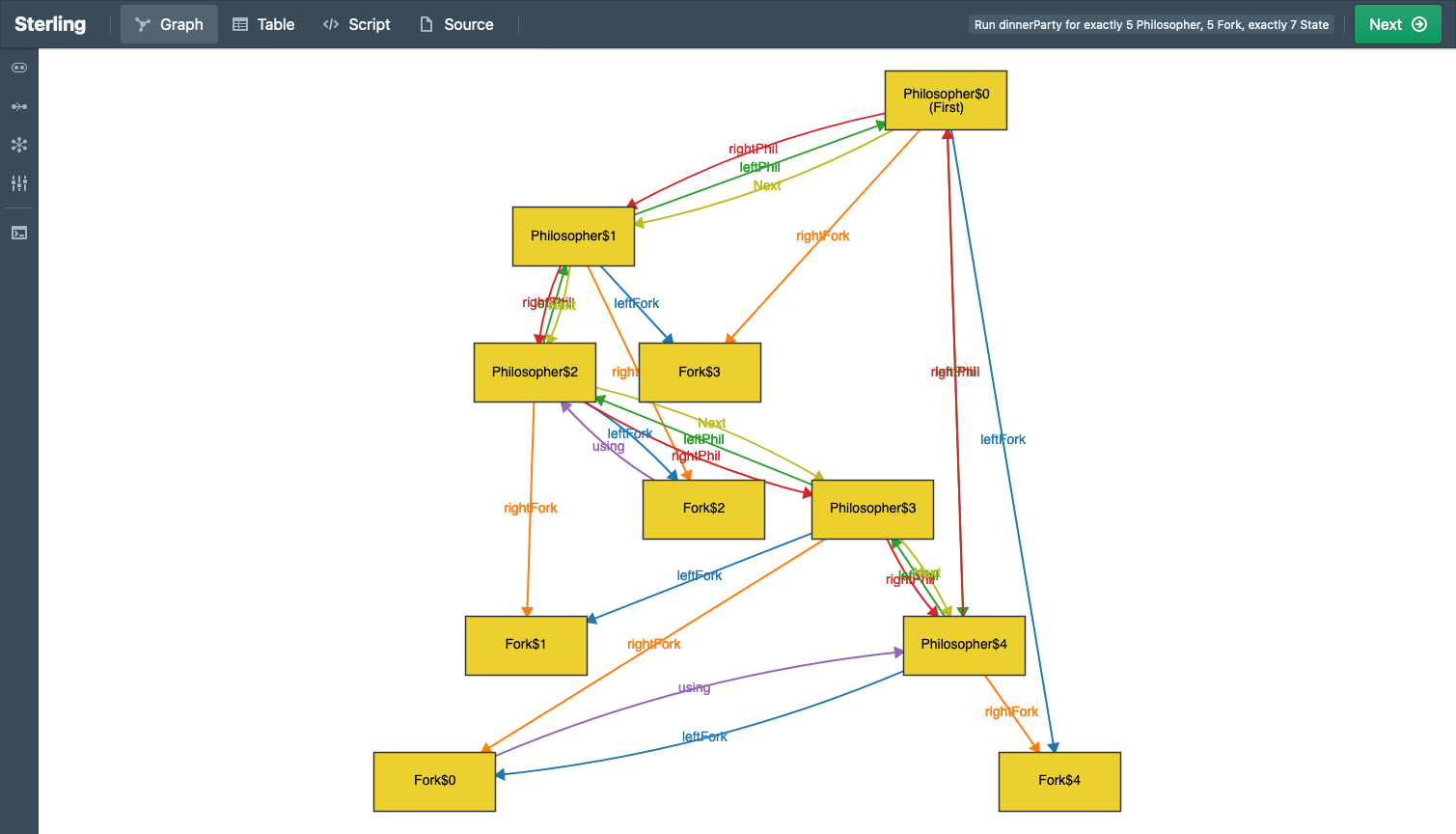
Default Sterling output

Here’s what custom visualization shows:

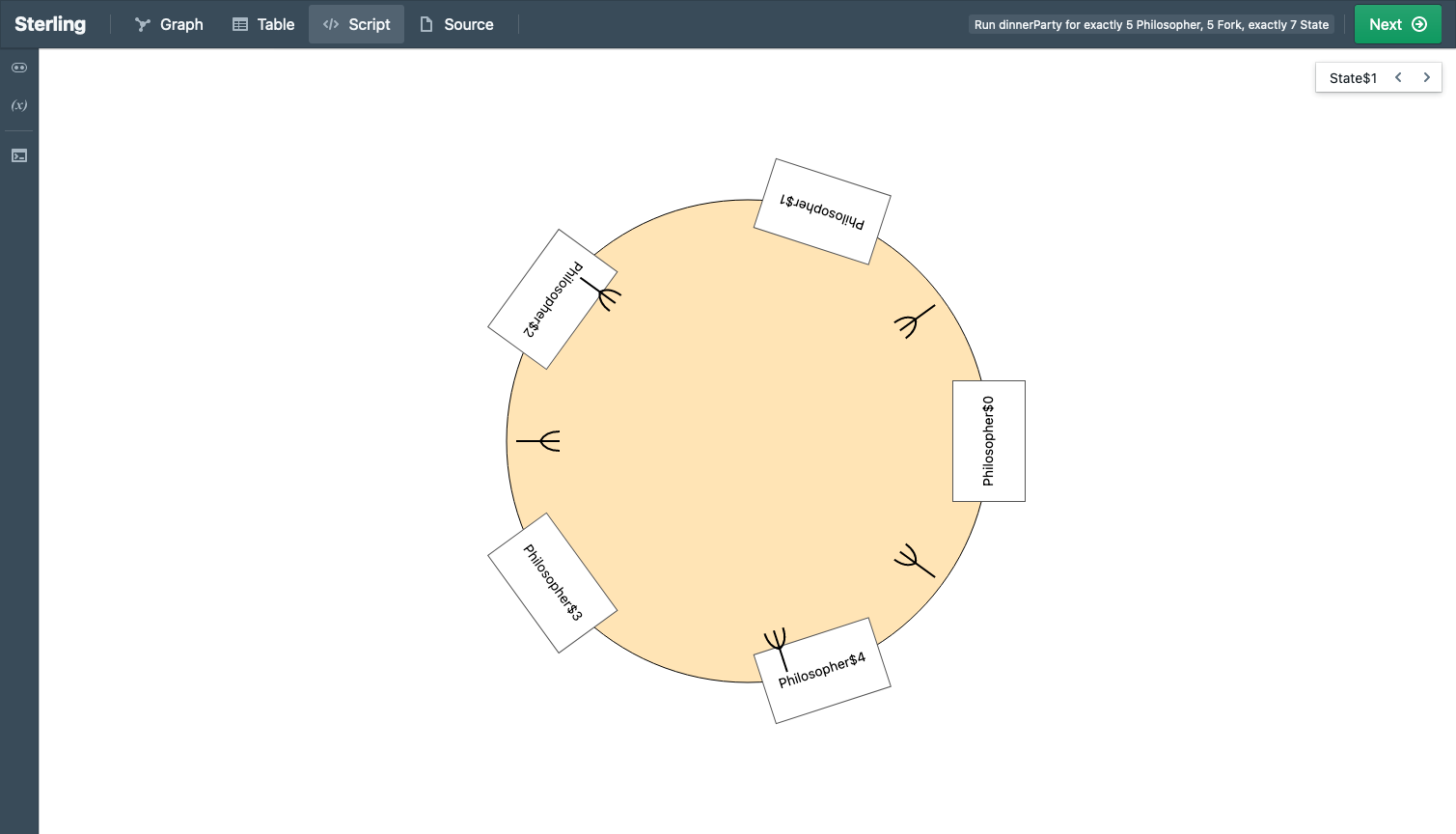
Custom Sterling output

See the difference?

For more details, see the paper. And please try out Forge!

Acknowledgements

We are grateful for support from the U.S. National Science Foundation (award #2208731).

Generating Programs Trivially: Student Use of Large Language Models

Tags: Large Language Models, Education, Formal Methods, Properties, Testing, User Studies

Posted on 19 September 2023.

The advent of large language models like GPT-3 has led to growing concern from educators about how these models can be used and abused by students in order to help with their homework. In computer science, much of this concern centers on how LLMs automatically generate programs in response to textual prompts. Some institutions have gone as far as instituting wholesale bans on the use of the tool. Despite all the alarm, however, little is known about whether and how students actually use these tools.

In order to better understand the issue, we gave students in an upper-level formal methods course access to GPT-3 via a Visual Studio Code extension, and explicitly granted them permission to use the tool for course work. In order to mitigate any equity issues around access, we allocated $2500 in OpenAI credit for the course, enabling free access to the latest and greatest OpenAI models.

Can you guess the total dollar value of OpenAI credit used by students?

We then analyzed the outcomes of this intervention, how and why students actually did and did not use the LLM.

Which of these graphs do you think best represents student use of GPT models over the semester?

When surveyed, students overwhelmingly expressed concerns about using GPT to help with their homework. Dominant themes included:

  • Fear that using LLMs would detract from learning.
  • Unfamiliarity with LLMs and issues with output correctness.
  • Fear of breaking course rules, despite being granted explicit permission to use GPT.

Much ink has been spilt on the effect of LLMs in education. While our experiment focuses only on a single course offering, we believe it can help re-balance the public narrative about such tools. Student use of LLMs may be influenced by two opposing forces. On one hand, competition for jobs may cause students to feel they must have “perfect” transcripts, which can be aided by leaning on an LLM. On the other, students may realize that getting an attractive job is hard, and decide they need to learn more in order to pass interviews and perform well to retain their positions.

You can learn more about the work from the paper.

Automated, Targeted Testing of Property-Based Testing Predicates

Tags: Formal Methods, Properties, Testing, Verification

Posted on 24 November 2021.

Property-Based Testing (PBT) is not only a valuable sofware quality improvement method in its own right, it’s a critical bridge between traditional software development practices (like unit testing) and formal specification. We discuss this in our previous work on assessing student performance on PBT. In particular, we introduce a mechanism to investigate how they do by decomposing the property into a collection of independent sub-properties. This gives us semantic insight into how students perform: rather than a binary scale, we can identify specific sub-properties that they may have difficulty with.

While this preliminary work was very useful, it suffered from several problems, some of which are not surprising while others became clear to us only in retrospect. In light of that, our new work makes several improvements.

  1. The previous work expected each of the sub-properties to be independent. However, this is too strong a requirement. For one, it masks problems that can lurk in the conjunction of sub-properties. The other problem is more subtle: when you see a surprising or intriguing student error, you want to add a sub-property that would catch that error, so you can generate statistics on it. However, there’s no reason the new property will be independent; in fact, it almost certainly won’t be.

  2. Our tests were being generated by hand, with one exception that was so subtle, we employed Alloy to find the test. Why only once? Why not use Alloy to generate tests in all situations? And while we’re at it, why not also use a generator from a PBT framework (specifically, Hypothesis)?

  3. And if we’re going to use both value-based and SAT-based example generators, why not compare them?

This new paper does all of the above. It results in a much more flexible, useful tool for assessing student PBT performance. Second, it revisits our previous findings about student performance. Third, it lays out architectures for PBT evaluation using SAT and a PBT-generator (specifically Hypothesis). In the process it explains various engineering issues we needed to address. Fourth, it compares the two approaches; it also compares how the two approaches did relative to hand-curated test suites.

You can read about all this in our paper.

Teaching and Assessing Property-Based Testing

Tags: Education, Formal Methods, Properties, Testing, User Studies

Posted on 10 January 2021.

Property-Based Testing (PBT) sees increasing use in industry, but lags significantly behind in education. Many academics have never even heard of it. This isn’t surprising; computing education still hasn’t come to terms with even basic software testing, even when it can address pedagogic problems. So this lag is predictable.

The Problem of Examples

But even people who want to use it often struggle to find good examples of it. Reversing a list drives people to drink, and math examples are hard to relate to. This is a problem from several respects. Without compelling examples, nobody will want to teach it. Even if they do, unless the examples are compelling, students will not pay attention to it. And if the students don’t, they won’t recognize opportunities to use it later in their careers.

This loses much more than a testing technique. We consider PBT a gateway to formal specification. Like a formal spec, it’s an abstract statement about behaviors. Unlike a formal spec, it doesn’t require learning a new language or mathematical formalism, it’s executable, and it produces concrete counter-examples. We therefore use it, in Brown’s Logic for Systems course, as the starting point to more formal specifications. (If they learn nothing about formal specification but simply become better testers, we’d still consider that a win.)

Therefore, for the past 10 years, and with growing emphasis, we’ve been teaching PBT: starting in our accelerated introductory course, then in Logic for Systems, and gradually in other courses as well. But how do we motivate the concept?

Relational Problems

We motivate PBT through what we call relational problems. What are those?

Think about your typical unit test. You write an input-output pair: f(x) is y. Let’s say it fails:

  • Usually, the function f is wrong. Congrats, you’ve just caught a bug!

  • Sometimes, the test is wrong: f(x) is not, in fact, y. This can take some reflection, and possibly reveals a misunderstanding of the problem.

That’s usually where the unit-testing story ends. However, there is one more possibility:

  • Neither is “wrong”. f(x) has multiple legal results, w, y, and z; your test chose y, but this particular implementation happened to return z or w instead.

We call these “relational” because f is clearly more a relation than a function.

Some Examples

So far, so abstract. But many problems in computing actually have a relational flavor:

  • Consider computing shortest paths in a graph or network; there can be many shortest paths, not just one. If we write a test to check for one particular path, we could easily run into the problem above.

  • Many other graph algorithms are also relational. There are many legal answers, and the implementation happens to pick just one of them.

  • Non-deterministic data structures inspire relational behavior.

  • Various kinds of matching problems—e.g., the stable-marriage problem—are relational.

  • Combinatorial optimization problems are relational.

  • Even sorting, when done over non-atomic data, is relational.

In short, computing is full of relational problems. While they are not at all the only context in which PBT makes sense, they certainly provide a rich collection of problems that students already study that can be used to expose this idea in a non-trivial setting.

Assessing Student Performance

Okay, so we’ve been having students write PBT for several years now. But how well do they do? How do we go about measuring such a question? (Course grades are far too coarse, and even assignment grades may include various criteria—like code style—that are not strictly germane to this question.) Naturally, their core product is a binary classifier—it labels a purported implementation as valid or invalid—so we could compute precision and recall. However, these measures still fail to offer any semantic insight into how students did and what they missed.

We therefore created a new framework for assessing this. To wit, we took each problem’s abstract property statement (viewed as a formal specification), and sub-divided it into a set of sub-properties whose conjunction is the original property. Each sub-property was then turned into a test suite, which accepted those validators that enforced the property and rejected those that did not. This let us get a more fine-grained understanding of how students did, and what kinds of mistakes they made.

Want to Learn More?

If you’re interested in this, and in the outcomes, please see our paper.

What’s Next?

The results in this paper are interesting but preliminary. Our follow-up work describes limitations to the approach presented here, thereby improving the quality of evaluation, and also innovates in the generation of classifying tests. Check it out!