Articles by tag: Education
Iterative Student Program Planning using Transformer-Driven Feedback
Forge: A Tool to Teach Formal Methods
Finding and Fixing Standard Misconceptions About Program Behavior
Profiling Programming Language Learning
The Examplar Project: A Summary
Observations on the Design of Program Planning Notations for Students
Conceptual Mutation Testing
Generating Programs Trivially: Student Use of Large Language Models
A Grounded Conceptual Model for Ownership Types in Rust
What Happens When Students Switch (Functional) Languages
Identifying Problem Misconceptions
Performance Preconceptions
Structural Versus Pipeline Composition of Higher-Order Functions
Plan Composition Using Higher-Order Functions
Towards a Notional Machine for Runtime Stacks and Scope
Student Help-Seeking for (Un)Specified Behaviors
Adding Function Transformers to CODAP
Developing Behavioral Concepts of Higher-Order Functions
Adversarial Thinking Early in Post-Secondary Education
Teaching and Assessing Property-Based Testing
Students Testing Without Coercion
Using Design Alternatives to Learn About Data Organizations
What Help Do Students Seek in TA Office Hours?
Combating Misconceptions by Encouraging Example-Writing
The Hidden Perils of Automated Assessment
Mystery Languages
The Pyret Programming Language: Why Pyret?
In-flow Peer Review: An Overview
CS Student Work/Sleep Habits Revealed As Possibly Dangerously Normal
From MOOC Students to Researchers
The New MOOR's Law
Essentials of Garbage Collection
LTL Tutor
Tags: Linear Temporal Logic, Education, Formal Methods, Misconceptions, Properties, Tools, Verification
Posted on 08 August 2024.We have been engaged in a multi-year project to improve education in Linear Temporal Logic (LTL) [Blog Post 1, Blog Post 2]. In particular, we have arrived at a detailed understanding of typical misconceptions that learners and even experts have. Our useful outcome from our studies is a set of instruments (think “quizzes”) that instructors can deploy in their classes to understand how well their students understand the logic and what weaknesses they have.
However, as educators, we recognize that it isn’t always easy to add new materials to classes. Furthermore, your students make certain mistakes—now what? They need explanations of what went wrong, need additional drill problems, and need checks whether they got the additional ones right. It’s hard for an educator to make time for all that. And if one is an independent learner, they don’t even have access to such educators.
Recognizing these practical difficulties, we have distilled our group’s expertise in LTL into a free online tutor:
We have leveraged insights from our studies to create a tool designed to be used by learners with minimal prior instruction. All you need is a brief introduction to LTL (or even just propositional logic) to get started. As an instructor, you can deliver your usual lecture on the topic (using your preferred framing), and then have your students use the tool to grow and to reinforce their learning.
In contrast to traditional tutoring systems, which are often tied to a specific curriculum or course, our tutor adaptively generates multiple-choice question-sets in the context of common LTL misconceptions.
- The tutor provides students who get a question wrong with feedback in terms of their answer’s relationship to the correct answer. Feedback can take the form of visual metaphors, counterexamples, or an interactive trace-stepper that shows the evaluation of an LTL formula across time.

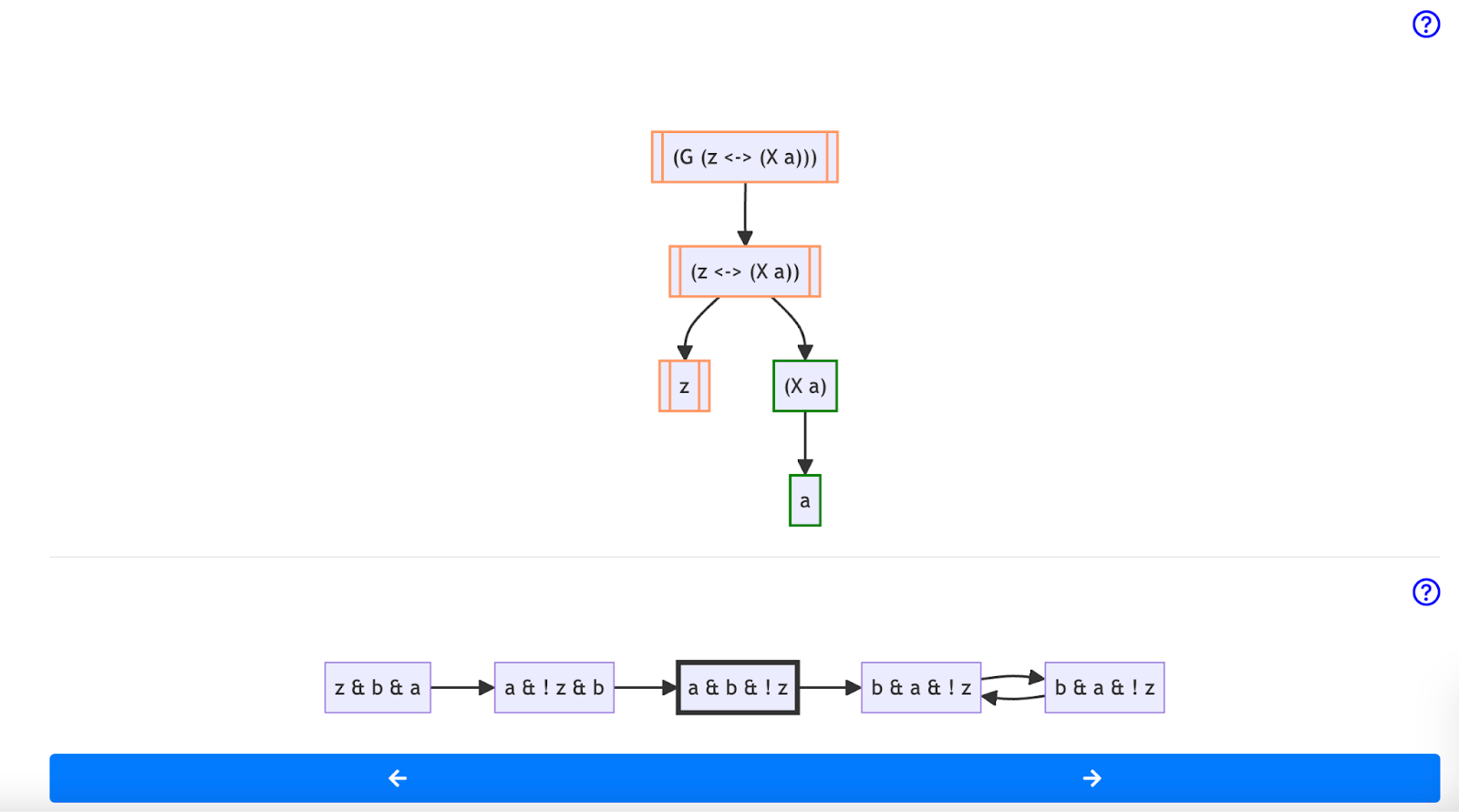
(G (z <-> X(a))) in the third state of a trace. While the overall formula is not satisfied at this moment in time, the sub-formula (X a) is satisfied. This allows learners to explore where their understanding of a formula may have diverged from the correct answer.
- If learners consistently demonstrate the same misconception, the tutor provides them further insight in the form of tailored text grounded in our previous research.
- Once it has a history of misconceptions exhibited by the student, the tutor generates novel, personalized question sets designed to drill students on their specific weaknesses. As students use the tutor, the system updates its understanding of their evolving needs, generating question sets to address newly uncovered or pertinent areas of difficulty.
We also designed the LTL Tutor with practical instructor needs in mind:
- Curriculum Agnostic: The LTL Tutor is flexible and not tied to any specific curriculum. You can seamlessly integrate it into your existing course without making significant changes. It both generates exercises for students and allows you to import your own problem sets.
- Detailed Reporting: To track your class’s progress effectively, you can create a unique course code for your students to enter, so you can get detailed insights into their performance.
- Self-Hostable: If you prefer to have full control over your data, the LTL Tutor can easily be self-hosted.
To learn more about the Tutor, please read our paper!
Iterative Student Program Planning using Transformer-Driven Feedback
Tags: Large Language Models, Education, Program Planning, User Studies
Posted on 05 July 2024.We’ve had a few projects now that address this idea of teaching students to plan out solutions to programming problems. A thus-far missing but critical piece is feedback on this planning process. Ideally we want to give students feedback on their plans before they commit to any code details. Our early studies had students express their plans in a semi-formalized way which would’ve allowed us to automatically generate feedback based on formal structure. However, our most recent project highlighted a strong preference towards more freedom in notation, with plans expressed in far less structured language. This presents a challenge when designing automated feedback.
So how do we interpret plans written with little to no restrictions on notation or structure, in order to still give feedback? We throw it at an LLM, right?
It’s never that simple. We first tried direct LLM feedback, handing the student plan to an LLM with instructions of what kinds of feedback to give. Preliminary feedback results ranged from helpful to useless to incorrect. Even worse, we couldn’t prevent the LLM from directly including a correct answer in its response.
So we built a different kind of feedback system. Student plans, expressed mostly in English, are translated into code via an LLM. (We do not allow the LLM to access the problem statement— otherwise it would silently correct student misconceptions when translating into code.) The resulting code is run against an instructor test suite, and the test suite results are shown to the student as feedback.
When we deployed this system, we found that the results from running the LLM-generated code against our instructor test suite seemed to serve as a useful proxy for student plan correctness. However, many issues from the LLM still caused a great deal of student frustration, especially from the LLM not having access to details from the problem statement.
LLMs are good at presenting correct code solutions and correcting errors, and there is clear incentive for these behaviors to improve. But these behaviors are sometimes counterproductive to student feedback. Creating LLM-based feedback systems still requires careful thought in both its design and presentation to students.
For more detail on our design and results, read here.
Forge: A Tool to Teach Formal Methods
Tags: Education, Formal Methods, Properties, Tools, User Studies, Verification, Visualization
Posted on 21 April 2024.For the past decade we have been studying how best to get students into formal methods (FM). Our focus is not on the 10% or so of students who will automatically gravitate towards it, but on the “other 90%” who don’t view it as a fundamental part of their existence (or of the universe). In particular, we decided to infuse FM thinking into the students who go off to build systems. Hence the course, Logic for Systems.
The bulk of the course focuses on solver-based formal methods. In particular, we began by using Alloy. Alloy comes with numerous benefits: it feels like a programming language, it can “Run” code like an IDE, it can be used for both verification and state-exploration, it comes with a nice visualizer, and it allows lightweight exploration with gradual refinement.
Unfortunately, over the years we have also run into various issues with Alloy, a full catalog of which is in the paper. In response, we have built a new FM tool called Forge. Forge is distinguished by the following three features:
-
Rather than plunging students into the full complexity of Alloy’s language, we instead layer it into a series of language levels.
-
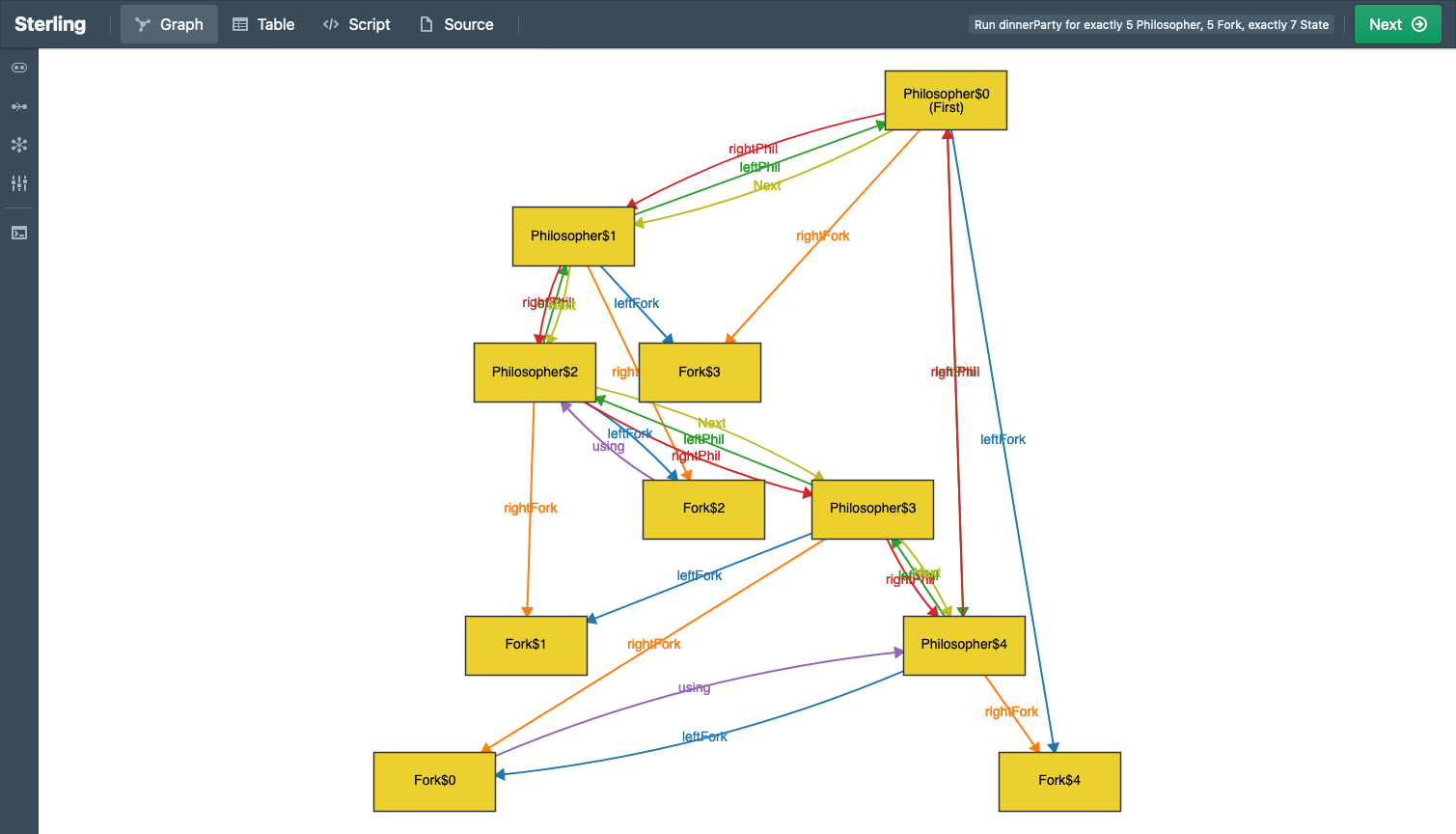
We use the Sterling visualizer by default, which you can think of as a better version of Alloy’s visualizer. But there’s much more! Sterling allows you to craft custom visualizations. We use this to create domain-specific visualizations. As we show in the paper, the default visualization can produce unhelpful, confusing, or even outright misleading images. Custom visualization takes care of these.
-
In the past, we have explored property-based testing as a way to get students on the road from programming to FM. In turn, we are asking the question, “What does testing look like in this FM setting?” Forge provides preliminary answers, with more to come.
Just to whet your appetite, here is an example of what a default Sterling output looks like (Alloy’s visualizer would produce something similar, with fewer distinct colors, making it arguably even harder to see):
Here’s what custom visualization shows:
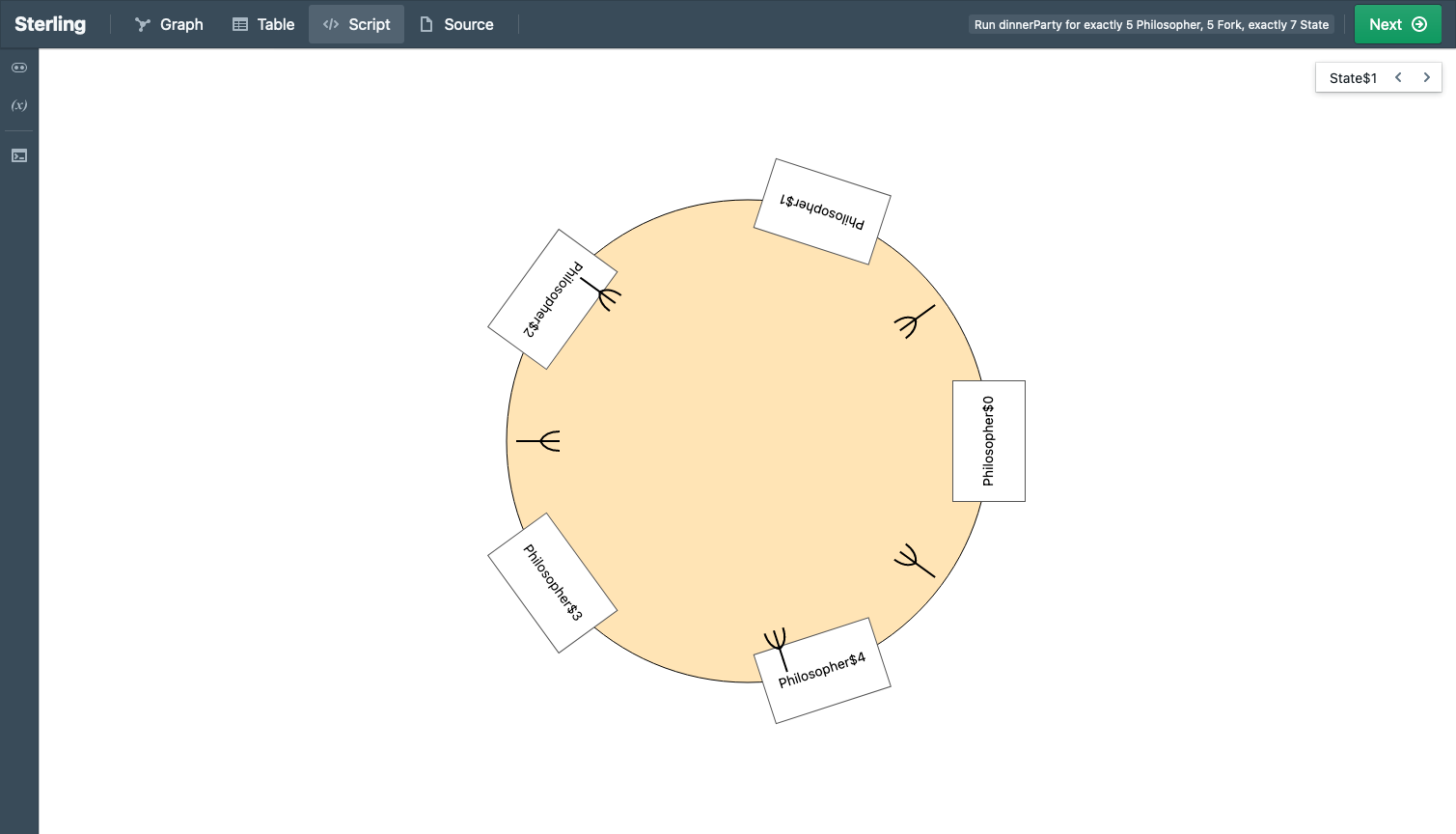
See the difference?
For more details, see the paper. And please try out Forge!
Acknowledgements
We are grateful for support from the U.S. National Science Foundation (award #2208731).
Finding and Fixing Standard Misconceptions About Program Behavior
Tags: Education, Misconceptions, Semantics, Tools, User Studies
Posted on 12 April 2024.A large number of modern languages — from Java and C# to Python and JavaScript to Racket and OCaml — share a common semantic core:
- variables are lexically scoped
- scope can be nested
- evaluation is eager
- evaluation is sequential (per “thread”)
- variables are mutable, but first-order
- structures (e.g., vectors/arrays and objects) are mutable, and first-class
- functions can be higher-order, and close over lexical bindings
- memory is managed automatically (e.g., garbage collection)
We call this the Standard Model of Languages (SMoL).
SMoL potentially has huge pedagogic benefit:
-
If students master SMoL, they have a good handle on the core of several of these languages.
-
Students may find it easier to port their knowledge between languages: instead of being lost in a sea of different syntax, they can find familiar signposts in the common semantic features. This may also make it easier to learn new languages.
-
The differences between the languages are thrown into sharper contrast.
-
Students can see that, by going beyond syntax, there are several big semantic ideas that underlie all these languages, many of which we consider “best practices” in programming language design.
We have therefore spent the past four years working on the pedagogy of SMoL:
-
Finding errors in the understanding of SMoL program behavior.
-
Finding the (mis)conceptions behind these errors.
-
Collating these into clean instruments that are easy to deploy.
-
Building a tutor to help students correct these misconceptions.
-
Validating all of the above.
We are now ready to present a checkpoint of this effort. We have distilled the essence of this work into a tool:
It identifies and tries to fix student misconceptions. The Tutor assumes users have a baseline of programming knowledge typically found after 1–2 courses: variables, assignments, structured values (like vectors/arrays), functions, and higher-order functions (lambdas). Unlike most tutors, instead of teaching these concepts, it investigates how well the user actually understands them. Wherever the user makes a mistake, the tutor uses an educational device called a refutation text to help them understand where they went wrong and to correct their conception. The Tutor lets the user switch between multiple syntaxes, both so they can work with whichever they find most comfortable (so that syntactic unfamiliarity or discomfort does not itself become a source of errors), and so they can see the semantic unity beneath these languages.
Along the way, to better classify student responses, we invent a concept called the misinterpreter. A misinterpreter is an intentionally incorrect interpreter. Concretely, for each misconception, we create a corresponding misinterpreter: one that has the same semantics as SMoL except on that one feature, where it implements the misconception instead of the correct concept. By making misconceptions executable, we can mechanically check whether student responses correspond to a misconception.
There are many interesting lessons here:
-
Many of the problematic programs are likely to be startlingly simple to experts.
-
The combination of state, aliasing, and functions is complicated for students. (Yet most introductory courses plunge students into this maelstrom of topics without a second thought or care.)
-
Misinterpreters are an interesting concept in their own right, and are likely to have value independent of the above use.
In addition, we have not directly studied the following claims but believe they are well warranted based on observations from this work and from experience teaching and discussing programming languages:
-
In SMoL languages, local and top-level bindings behave the same as the binding induced by a function call. However, students often do not realize that these have a uniform semantics. In part this may be caused by our focus on the “call by” terminology, which focuses on calls (and makes them seem special). We believe it would be an improvement to replace these with “bind by”.
-
We also believe that the terms “call-by-value” and “call-by-reference” are so hopelessly muddled at this point (between students, instructors, blogs, the Web…) that finding better terminology overall would be helpful.
-
The way we informally talk about programming concepts (like “pass a variable”), and the syntactic choices our languages make (like
return x), are almost certainly also sources of confusion. The former can naturally lead students to believe variables are being aliased, and the latter can lead them to believe the variable, rather than its value, is being returned.
For more details about the work, see the paper. The paper is based on an old version of the Tutor, where all programs were presented in parenthetical syntax. The Tutor now supports multiple syntaxes, so you don’t have to worry about being constrained by that. Indeed, it’s being used right now in a course that uses Scala 3.
Most of all, the SMoL Tutor is free to use! We welcome and encourage instructors of programming courses to consider using it — you may be surprised by the mistakes your students make on these seemingly very simple programs. But we also welcome learners of all stripes to give it a try!
Profiling Programming Language Learning
Tags: Education, Rust, User Studies
Posted on 01 February 2024.Programmers profile programs. They use profiling when they suspect a program is not being as effective (performant) as they would like. Profiling helps them track down what is working well and what needs more work, and how best to use their time to make the program more effective.
Programming language creators want their languages to be adopted. To that end, they create documentation, such as a book or similar written document. These are written with the best of intentions and following the best practices they know of. But are they effective? Are they engaging? How do they know? These are questions very much in the Socio-PLT mould proposed by Meyerovich and Rabkin.
In addition, their goal in writing such documentation is that people learn about their language. But many people do not enjoy a passive reading experience or, even if they do, they won’t learn much from it.
These two issues mesh together well. Books should be more interactive. Books should periodically stop readers and encourage them to think about what they’re reading:
If a listener nods his head when you’re explaining your program, wake him up.
—Alan Perlis
Books should give readers feedback on how well they have been reading so far. And authors should use this information to drive the content of the book.
We have been doing this in our Rust Book experiment. There, the focus was on a single topic: ownership. But in fact we have been doing this across the whole book, and in doing so we have learned a great deal.
-
We analyzed the trajectory of readers and showed that many drop out when faced with difficult language concepts like Rust’s ownership types. This suggests either revising how those concepts are presented, moving them later in the book, or splitting them into two parts, a gentle introduction that retains readers and a more detailed, more technical chapter later in the book once readers are more thoroughly invested.
-
We used both classical test theory and item response theory to analyze the characteristics of quiz questions. We found that better questions are more conceptual in nature, such as asking why a program does not compile versus whether a program compiles.
-
We performed 12 interventions into the book to help readers with difficult questions. We evaluated how well an intervention worked by comparing the performance of readers pre- and post-intervention on the question being targeted.
In other words, the profiler analogy holds: it helps us understand the behavior of “the program” (namely, users going through the book), suggests ways to improve it, and helps us analyze specific attempts at improvement and shows that they are indeed helpful.
However, we did all this with a book for which, over 13 months, 62,526 readers answered questions 1,140,202 times. This is of no help to new languages who might struggle to get more than dozens of users! Therefore, we sampled to simulate how well we would have fared on much smaller subsets of users. We show that for some of our analyses even 100 users would suffice, while others require around a 1000. These numbers—especially 100—are very much attainable for young languages.
Languages are designed for adoption, but mere design is usually insufficient to enable it, as the Socio-PLT paper demonstrated. We hope work along these lines can help language designers get their interesting work into many more hands and minds.
For more details, see the paper. Most of all, you can do this with your materials, too! The library for adding these quizzes is available here.
The Examplar Project: A Summary
Tags: Education, Misconceptions, Testing, Tools
Posted on 01 January 2024.For the past several years, we have worked on a project called Examplar. This article summarizes the goals and methods of the project and provides pointers to more detailed articles describing it.
Context
When faced with an programming problem, computer science students all-too-often begin their implementations with an incomplete understanding of what the problem is asking, and may not realize until far into their development process (if at all) that they have solved the wrong problem. At best, a student realizes their mistake, suffers from some frustration, and is able to correct it before the final submission deadline. At worst, they might not realize their mistake until they receive feedback on their final submission, depriving them of the intended learning goal of the assignment.
How can we help them with this? A common practice—used across disciplines—is to tell students, “explain the problem in your own words”. This is a fine strategy, except it demands far too much of the student. Any educator who has done this knows that most students rightly stumble through this exercise, usually because they don’t have any better words than are already in the problem statement. So what was meant to be a comprehension exercise becomes a literary one; even if they can restate it very articulately, it may be because of verbal skills, not necessarily indicative of good understanding. And for complex problems, the whole exercise is somewhat futile. It’s all made even more difficult when students are not in their native language, etc.
So we have the kernel of a good idea—asking students to read back their understanding—but words are a poor medium for it.
Examples
Our idea is that writing examples—using the syntax of text cases—is a great way to express understanding:
-
Examples are concrete.
-
It’s hard to be vague.
-
Difficulty writing down examples is usually indicative of broader difficulties with the problem, and a great, concrete way to initiate a discussion with course staff.
-
It gets a head-start on writing tests, which too many computing curricula undervalue (if they tackle it at all).
Best of all, because the examples are executable, they can be run against implementations so that students get immediate feedback.
Types of Feedback
We want to give two kinds of feedback:
-
Correctness: Are they even correct? Do they match the problem specification?
-
Thoroughness: How much of the problem space do they cover? Do they dodge misconceptions?
Consider (for example!) the median function. Here are two examples, in the syntax of Pyret:
check:
median([list: 1, 2, 3]) is 2
median([list: 1, 3, 5]) is 3
end
These are both correct, as running them against a correct implementation of median will confirm, but are they thorough?
A student could, for instance, easily mistake median for mean. Note that the two examples above do not distinguish between the two functions! So giving students a thumbs-up at this point may still send them down the wrong path: they haven’t expressed enough of an understanding of the problem.
Evaluating Examples
For this reason, Examplar runs a program against multiple implementations. One is a correct implementation (which we call the wheat). (For technical reasons, it can be useful to have more than one correct implementation; see more below.) There are also several buggy implementations (called chaffs). Each example is first run against the wheat, to make sure it conforms to the problem specification. It is then run against each of the chaffs. Here’s what a recent version looks like:
Every example is a classifier: its job is to classify a program as correct or incorrect, i.e., to separate the wheat from the chaff. Of course, a particular buggy implementation may not be buggy in a way that a particular example catches. But across the board, the collection of examples should do a fairly good job of catching the buggy examples.
Thus, for instance, one of our buggy implementations of median would be mean. Because the two examples above are consistent with mean as well, they would (incorrectly) pass mean instead of signaling an error. If we had no other examples in our suite, we would fail to catch mean as buggy. That reflects directly as “the student has not yet confirmed that they understand the difference between the two functions”. We would want students to add examples like
median([list: 1, 3, 7]) is 3
that pass median but not mean to demonstrate that they have that understanding.
Answering Questions
Examplar is also useful as a “24 hour TA”. Consider this example:
median([list: 1, 2, 3, 4]) is ???
What is the answer? There are three possible answers: the left-median (2), right-median (3), and mean-median (2.5). A student could post on a forum and wait for a course staffer to read and answer. Or they can simply formulate the question as a test: e.g.,
median([list: 1, 2, 3, 4]) is 2.5
One of these three will pass the wheat. That tells the student the definition being used for this course, which may not have been fully specified in the problem statement. Similarly:
median([list: ]) is ??? # the empty list
Indeed, we see students coming to course staff with questions like, “I see that Examplar said that …, and I wanted to know why this is the answer”, which is a fantastic kind of question to hear.
Whence Chaffs?
It’s easy to see where to get the wheat: it’s just a correct implementation of the problem. But how do we get chaffs?
An astute reader will have noticed that we are practicing a form of mutation testing. Therefore, it might be tempting to use mutation testing libraries to generate chaffs. This would be a mistake because it misunderstands the point of Examplar.
We want students to use Examplar before they start programming, and as a warm-up activity to get their minds into the right problem space. That is not the time to be developing a test suite so extensive that it can capture every strange kind of error that might arise. Rather, we think of Examplar as performing what we call conceptual mutation testing: we only want to make sure they have the right conception of the problem, and avoid misconceptions about it. Therefore, chaffs should correspond to high-level conceptual mistakes (like confusing median and mean), not low-level programming errors.
Whence Misconceptions?
There are many ways to find out what misconceptions students have. One is by studying the errors we ourselves make while formulating or solving the problem. Another is by seeing what kinds of questions they ask course staff and what corrections we need to make. But there’s one more interesting and subtle source: Examplar itself!
Remember how we said we want examples to first pass the wheat? The failing ones are obviously…well, they’re wrong, but they may be wrong for an interesting reason. For instance, suppose we’ve defined median to produce the mean-median. Now, if a student writes
median([list: 1, 2, 3, 4]) is 3
they are essentially expressing their belief that they need to solve the right-median problem. Thus, by harvesting these “errors”, filtering, and then clustering them, we can determine what misconceptions students have because they told us—in their own words!
Readings
-
Why you might want more than one wheat: paper
-
Student use without coercion (in other words, gamified interfaces help…sometimes a bit too much): blog; paper
-
What help do students need that Examplar can’t provide? blog; paper
But this work has much earlier origins:
-
How to Design Programs has students write tests before programs. However, these tests are inert (i.e., there’s nothing to run them against), so students see little value in doing so. Examplar eliminates this inertness, and goes further.
-
Before Examplar, we had students provide peer-review on tests, and found it had several benefits: paper. We also built a (no longer maintained) programming environment to support peer review: paper.
-
One thing we learned is that these test suites can grow too large to generate useful feedback. This caused us to focus on the essential test cases, out of which the idea of examples (as opposed to tests) evolved: paper.
Observations on the Design of Program Planning Notations for Students
Tags: Higher-Order Functions, Education, Program Planning, User Studies
Posted on 27 December 2023.In two recent projects we’ve tried to make progress on the long-dormant topic of teaching students how to plan programs. Concretely, we chose higher-order functions as our driving metaphor to address the problem of “What language shall we use to express plans?” We showed that this was a good medium for students. We also built some quite nice tool support atop Snap!. Finally, we were making progress on this long open issue!
Not so fast.
We tried to replicate our previous finding with a new population of students and somewhat (but not entirely) different problems. It didn’t work well at all. Students made extensive complaints about the tooling and, when given a choice, voted with their feet by not using it.
We then tried again, allowing them freedom in what notation they used, but suggesting two: one was diagrammatic (essentially representing dataflow), and the other was linear prose akin to a todo-list or recipe. Students largely chose the latter, and also did a better job with planning.
Overall, this is a sobering result. It diminishes some of our earlier success. At the same time, it sheds more light on the notations students prefer. In particular, it returns to our earlier problem: planning needs a vocabulary, and we are still far from establishing one that students find comfortable and can use successfully. But it also highlights deeper issues, such as the need to better support students with composition. Critically, composition serves as a bridge between more plan-oriented students and bricoleurs, making it especially worthy of more study, no matter your position on how students should or do design programs.
For more details, see the paper.
Conceptual Mutation Testing
Tags: Education, Misconceptions, Testing, Tools, User Studies
Posted on 31 October 2023.Here’s a summary of the full arc, including later work, of the Examplar project.
The Examplar system is designed to solve the documented phenomenon that students often misunderstand a programming problem statement and hence “solve” the wrong problem. It does so by asking students to begin by writing input/output examples of program behavior, and evaluating them against correct and buggy implementations of the solution. Students refine and demonstrate their understanding of the problem by writing examples that correctly classify these implementations.

It is, however, very difficult to come up with good buggy candidates. These programs must correspond to the problem misconceptions students are most likely to have. Students can, otherwise, end up spending too much time catching them, and not enough time on the actual programming task. Additionally, a small number of very effective buggy implementations is far more useful than either a large number or ineffective ones (much less both).
Our previous research has shown that student-authored examples that fail the correct implementation often correspond to student misconceptions. Buggy implementations based on these misconceptions circumvent many of the pitfalls of expert-generated equivalents (most notably the ‘expert blind spot’). That work, however, leaves unanswered the crucial question of how to operationalize class-sourced misconceptions. Even a modestly sized class can generate thousands of failing examples per assignment. It takes a huge amount of manual effort, expertise, and time to extract misconceptions from this sea of failing examples.
The key is to cluster these failing examples. The obvious clustering method – syntactic – fails miserably: small syntactic differences can result in large semantic differences, and vice versa (as the paper shows). Instead, we need a clustering technique that is based on the semantics of the problem.
This paper instead presents a conceptual clustering technique based on key characteristics of each programming assignment. These clusters dramatically shrink the space that must be examined by course staff, and naturally suggest techniques for choosing buggy implementation suites. We demonstrate that these curated buggy implementations better reflect student misunderstandings than those generated purely by course staff. Finally, the paper suggests further avenues for operationalizing student misconceptions, including the generation of targeted hints.
You can learn more about the work from the paper.
Generating Programs Trivially: Student Use of Large Language Models
Tags: Large Language Models, Education, Formal Methods, Properties, Testing, User Studies
Posted on 19 September 2023.The advent of large language models like GPT-3 has led to growing concern from educators about how these models can be used and abused by students in order to help with their homework. In computer science, much of this concern centers on how LLMs automatically generate programs in response to textual prompts. Some institutions have gone as far as instituting wholesale bans on the use of the tool. Despite all the alarm, however, little is known about whether and how students actually use these tools.
In order to better understand the issue, we gave students in an upper-level formal methods course access to GPT-3 via a Visual Studio Code extension, and explicitly granted them permission to use the tool for course work. In order to mitigate any equity issues around access, we allocated $2500 in OpenAI credit for the course, enabling free access to the latest and greatest OpenAI models.
Can you guess the total dollar value of OpenAI credit used by students?
We then analyzed the outcomes of this intervention, how and why students actually did and did not use the LLM.
Which of these graphs do you think best represents student use of GPT models over the semester?
When surveyed, students overwhelmingly expressed concerns about using GPT to help with their homework. Dominant themes included:
- Fear that using LLMs would detract from learning.
- Unfamiliarity with LLMs and issues with output correctness.
- Fear of breaking course rules, despite being granted explicit permission to use GPT.
Much ink has been spilt on the effect of LLMs in education. While our experiment focuses only on a single course offering, we believe it can help re-balance the public narrative about such tools. Student use of LLMs may be influenced by two opposing forces. On one hand, competition for jobs may cause students to feel they must have “perfect” transcripts, which can be aided by leaning on an LLM. On the other, students may realize that getting an attractive job is hard, and decide they need to learn more in order to pass interviews and perform well to retain their positions.
You can learn more about the work from the paper.
A Grounded Conceptual Model for Ownership Types in Rust
Tags: Crowdsourcing, Education, Rust, Types, User Studies, Visualization
Posted on 17 September 2023.Rust is establishing itself as the safe alternative to C and C++, making it an essential component for building a future software univers that is correct, reliable, and secure. Rust achieves this in part through the use of a sophisticated type system based on the concept of ownership. Unfortunately, ownership is unfamiliar to most conventionally-trained programmers. Surveys suggest that this central concept is also one of Rust’s most difficult, making it a chokepoint in software progress.
We have spent over a year understanding how ownership is currently taught, in what ways this proves insufficient for programmers, and looked for ways to improve their understanding. When confronted with a program containing an ownership violation, we found that Rust learners could generally predict the surface reason given by the compiler for rejecting the program. However, learners could often could not relate the surface reason to the underlying issues of memory safety and undefined behavior. This lack of understanding caused learners to struggle to idiomatically fix ownership errors.
To address this, we created a new conceptual model for Rust ownership, grounded in these studies. We then translated this model into two new visualizations: one to explain how the type-system works, the other to illustrate the impact on run-time behavior. Crucially, we configure the compiler to ignore borrow-checker errors. Through this, we are able to essentially run counterfactuals, and thereby illustrate the ensuing undefined behavior.
Here is an example of the type-system visualization:

And here is an example of the run-time visualization:
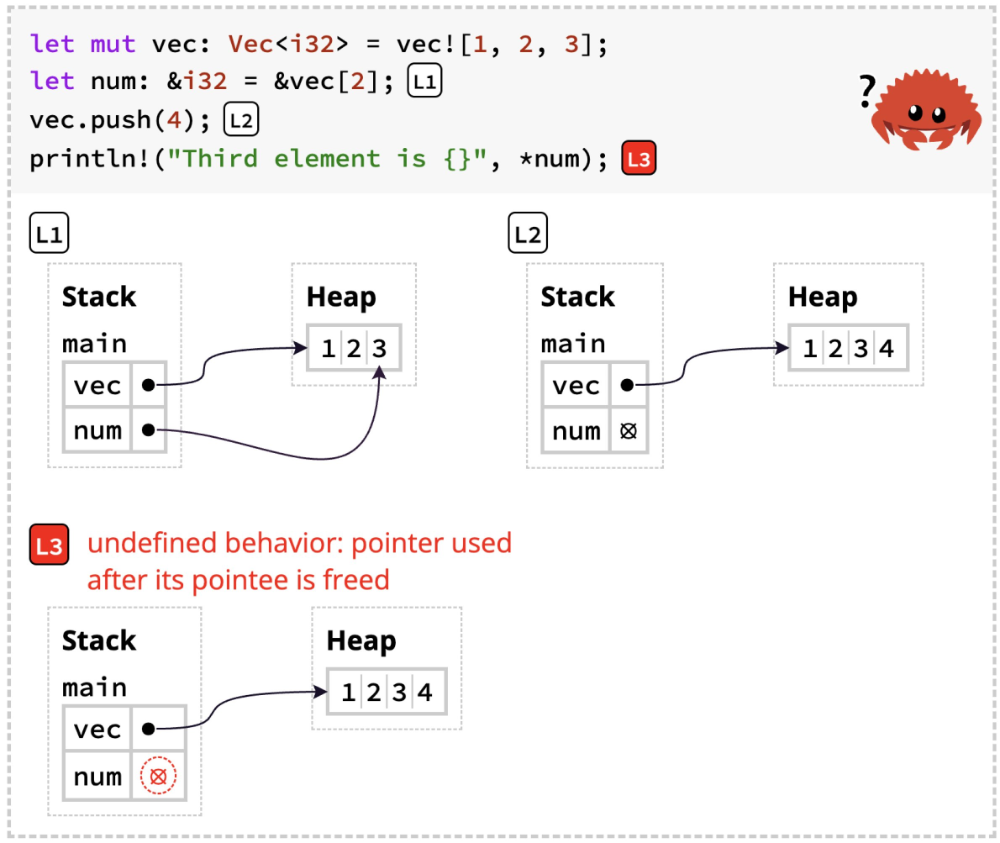
We incorporated these diagrams into an experimental version of The Rust Programming Language by Klabnik and Nichols. The authors graciously permitted us to create this fork and publicize it, and also provided a link to it from the official edition. As a result, we were able to test our tools on readers, and demonstrate that they do actually improve Rust learning.
The full details are in the paper. Our view is that the new tools are preliminary, and other researchers may come up with much better, more creative, and more effective versions of them. Rather, the main contribution is an understanding of how programmers do and don’t understand ownership, and in particular its relationship to undefined behavior. It is therefore possible that new pedagogies that make that connection clear may obviate the need for some of these tools entirely.
What Happens When Students Switch (Functional) Languages
Tags: Education, Pyret, Python, User Studies
Posted on 16 July 2023.What happens when students learn a second programming language after having gotten comfortable with one? This was a question of some interest in the 1980s and 1990s, but interest in it diminished. Recent work by Ethel Tshukudu and her collaborators have revived interest in this question.
Unfortunately, none of this work has really considered the role of functional programming. This is especially worth considering in the framework that Tshukudu’s work lays out, which is to separate syntax and semantics. That is the issue we tackle.
Specifically, we try to study two conditions:
-
different syntax, similar semantics
-
similar syntax, different semantics
For the same semantics, any two sufficiently syntactically different functional languages would do. The parenthetical syntax of the Lisp family gives us a syntax that is clearly different from the infix syntaxes of most other languages. In our particular case, we use Racket and Pyret.
The second case is trickier. For a controlled lab study, one could do this with very controlled artificial languages. However, we are interested in student experiences, which require curricula and materials that made-up languages usually cannot provide.
Instead, we find a compromise. The Pyret syntax was inspired by that of Python, though it does have some differences. It comes with all the curricular support we need. Therefore, we can compare it versus an imperative curriculum in Python.
You can read the details in the paper. The work is less interesting for its answers than for its setup. As a community we know very little about this topic. We hope the paper will inspire other educators both through the questions we have asked and the materials we have designed.
Identifying Problem Misconceptions
Tags: Education, Misconceptions, Testing, Tools
Posted on 15 October 2022.Here’s a summary of the full arc, including later work, of the Examplar project.
Our recent work is built on the documented research that students often misunderstand a programming problem statement and hence “solve” the wrong problem. This not only creates frustration and wastes time, it also robs them of whatever learning objective motivated the task.
To address this, the Examplar system asks students to first write examples. These examples are evaluated against wheats (correct implementations) and chaffs (buggy implementations). Examples must pass the wheat, and correctly identify as wrong as many chaffs as possible. Prior work explores this and shows that it is quite effective.
However, there’s a problem with chaffs. Students can end up spending too much time catching them, and not enough time on the actual programming task. Therefore, you want chaffs that correspond to the problem misconceptions students are most likely to have. Having a small number of very effective chaffs is far more useful than either a large number or ineffective ones (much less both). But the open question has always been, how do we obtain chaffs?
Previously, chaffs were created by hand by experts. This was problematic because it forces experts to imagine the kinds of problems students might have; this is not only hard, it is bound to run into expert blind spots. What other method do we have?
This work is based on a very simple, clever observation: any time an example fails a wheat, it may correspond to a student misconception. Of course, not all wheat failures are misconceptions! It could be a typo, it could be a basic logical error, or it could even be an attempt to game the wheat-chaff system. Do we know in what ratio these occur, and can we use the ones that are misconceptions?
This paper makes two main contributions:
-
It shows that that many wheat failures really are misconceptions.
-
It uses these misconceptions to formulate new chaffs, and shows that they compare very favorably to expert-generated chaffs.
Furthermore, the work spans two kinds of courses: one is an accelerated introductory programming class, while the other is an upper-level formal methods course. We show that there is value in both settings.
This is just a first step in this direction; a lot of manual work went into this research, which needs to be automated; we also need to measure the direct impact on students. But it’s a very promising direction in a few ways:
-
It presents a novel method for finding misconceptions.
-
It naturally works around expert blind-spots.
-
With more automation, it can be made lightweight.
In particular, if we can make it lightweight, we can apply it to settings—even individual homework problems—that also manifest misconceptions that need fixing, but could never afford heavyweight concept-inventory-like methods for identifying them.
You can learn more about the work from the paper.
Performance Preconceptions
Tags: Education, Misconceptions, User Studies
Posted on 10 October 2022.What do computer science students entering post-secondary (collegiate) education think “performance” means?
Who or what shapes these views?
How accurate are these views?
And how correctable are their mistakes?
These questions are not merely an idle curiosity. How students perceive performance impacts how they think about program design (e.g., they may think a particular design is better but still not use it because they think it’s less performant). It also affects their receptiveness to new programming languages and styles (“paradigms”) of programming. Anecdotally, we have seen exactly these phenomena at play in our courses.
We are especially interested in students who have had prior computer science (in secondary school), such as students taking the AP Computer Science exam in the US. These students often have significant prior computing, but we have studied relatively little about the downstream consequences of these courses. Indeed, performance considerations are manifest in material as early as the age 4–8 curriculum from Code.org!
This paper takes a first step in examining these issues. We find that students have high confidence in incorrect answers on material they should have little confidence about. To address these problems, we try multiple known techniques from the psychology and education literature — the Illusion of Explanatory Depth, and Refutation Texts — that have been found to work in several other domains. We see that they have little impact here.
This work has numerous potential confounds based on the study design and location of performance. Therefore, we don’t view this as a definitive result, but rather as a spur to start an urgently-needed conversation about factors that affect post-secondary computer science education. Concretely, as we discuss in the discussion sections, we also believe there is very little we know about how students conceive of “performance”, and question whether our classical methods for approaching it are effective.
The paper is split into a short paper, that summarizes the results, an an extensive appendix, which provides all the details and justifies the summary. Both are available online.
Structural Versus Pipeline Composition of Higher-Order Functions
Tags: Higher-Order Functions, Education, User Studies
Posted on 16 August 2022.Building on our prior work on behavioral conceptions of higher-order functions (HOFs), we have been looking now at their composition. In designing a study, we kept running into tricky problems in designing HOF composition problems. Eventually, we set out to study that question directly.
We’re going to give you a quiz. Imagine you have a set of standard
HOFs (map, filter, sort, andmap, ormap, take-while). You
are given two ways to think about composing them (where “funarg” is
short for the parameter that is a function):
Type A: HOF_A(<some funarg>, HOF_B(<some funarg>, L))
Type B: HOF_C((lambda (inner) HOF_D(<some funarg>, inner)), L)
-
Which of these would you consider “easier” for students to understand and use?
-
How would you rate their relative expressive power in terms of problems they can solve?
Don’t go on until you’ve committed to answers to these questions.
Rather than A and B, here are better names: we’ll refer to A
as pipeline, because it corresponds to a traditional
data-processing/Unix pipeline composition (HOF_B L | HOF_A), and
we’ll refer to B as structural. If you’re like many other people
we’ve asked, you likely think that pipeline is easier, but you’re less
certain about how to answer the second question.
Alright, now you’re ready to read the paper! We think the structural/pipeline distinction is similar to the structural/generative recursion distinction in HtDP, and similarly has consequences for how we order HOF composition in our pedagogy. We discuss all this, and more, in the document.
Plan Composition Using Higher-Order Functions
Tags: Higher-Order Functions, Education, Program Planning, User Studies
Posted on 09 July 2022.There is a long history of wanting to examine planning in computing education research, but relatively little work on it. One problem you run into when trying to do this seriously is: “What language shall we use to express plans?” A lot hinges on this language.
-
The programming language itself is too low-level: there are too many administrative details that get in the way and might distract the student; failures may then reflect these distractions, not an inability to plan.
-
Plain English may be too high-level. It’s both difficult to give any useful (automated) feedback about, it may also require too much interpretation. In particular, an expert may interpret student utterances in ways the student didn’t mean, thereby giving the student an OK signal when in fact the student is not on the right path.
Separately, in prior work, we looked at whether students are able to understand higher-order functions (HOFs) from a behavioral perspective: i.e., as atomic units of behavior without reference to their underlying implementation. For our population, we found that they generally did quite well.
You may now see how these dovetail. Once students have a behavioral understanding of individual HOFs, you can use them as a starting vocabulary for planning. Or to think in more mechanical terms, we want to study how well students understand the composition of HOFs. That is the subject of this work.
Concretely, we start by confirming our previous result—that they understand the building blocks—and can also articulate many of the features that we previously handed out to them. This latter step is important because any failures at composition may lie in their insufficiently rich understanding of the functions. Fortunately, we see that this is again not a problem with our population.
We then focus on the main question: can they compose these HOFs. We do this in two ways:
-
We give them input-output examples and ask them to identify which compositions of functions would have produced those results. This is akin to having a dataset you need to transform and knowing what you would like the result to look like, and figuring out what steps will take it there.
-
We give them programming problems to solve, and ask them to first provide high-level plans of their solutions.
What we find is that students don’t do superbly on (1), but do extremely well on (2). Indeed, our goal had been to study what changes between the planning and programming phase (e.g., if they planned incorrectly but programmed correctly; or vice versa), but our students unfortunately did too well on both to give us any useful data!
Of particular interest is how we got them to state plans. While HOFs are the “semantics”, we still need a “syntax” for writing them. Conventional textual programming has various bad affordances. Instead, we created a custom palette of operations in Snap!. In keeping with the point of this paper, the operations were HOFs. There are numerous advantages to this use of Snap!:
-
Drag-and-drop construction avoids getting bogged down in the vagaries of textual syntax.
-
Changing plans is much easier, because you can drag whole blocks and (again) not get caught up in messy textual details. This means students are hopefully more willing to change around their plans.
-
The planning operations focus on the operations we care about, and students can ignore irrelevant details.
-
Most subtly: the blanks can be filled in with text. That is, you get “operations on the outside, text on the inside”: at the point where things get too detailed, students can focus on presenting their ideas rather than on low-level details. This is, in other words, a hybrid of the two methods we suggested at the beginning.
Critically, these aren’t programs! Because of the text, they can’t be executed. But that’s okay! They’re only meant to help students think through their plans before starting to write the program. In particular, given students’ reluctance to change their programs much once they start coding, it seems especially important to give them a fluid medium—where switching costs are low—in which to plan things before they start to write a line of code. So one of the best things about this paper, beyond the main result, is actually our discovery of Snap!’s likely utility in this setting.
For more details, see the paper!
Towards a Notional Machine for Runtime Stacks and Scope
Tags: Education, Misconceptions, Scope, Semantics, User Studies
Posted on 07 July 2022.Stacks are central to our understanding of program behavior; so is scope. These concepts become ever more important as ever more programming languages embrace concepts like closures and advanced control (like generators). Furthermore, stacks and scope interact in an interesting way, and these features really exercise their intersection.
Over the years we’ve seen students exhibit several problematic conceptions about stacks (and scope). For instance, consider a program like this:
def f(x):
return g(x + 1)
def g(y):
return y + x
f(3)
What is its value? You want an error: that x is not bound. But think
about your canonical stack diagram for this program. You have a frame
for g atop that for x, and you have been told that you “look down
the stack”. (Or vice versa, depending on how your stacks grow.) So
it’s very reasonable to conclude that this program produces 7, the
result produced by dynamic scope.
We see students thinking exactly this.
Consider this program:
def f(x):
return lambda y: x + y
p = f(3)
p(4)
This one, conversely, should produce 7. But students who have been
taught a conventional notion of call-and-return assume that f’s
stack frame has been removed after the call completed (correct!), so
p(4) must result in an error that x is not bound.
We see students thinking exactly this, too.
The paper sets out to do several things.
First, we try to understand the conceptions of stacks that students have coming into an upper-level programming languages course. (It’s not great, y’all.)
Second, we create some tooling to help students learn more about stacks. More on that below. The tooling seems to work well for students who get some practice using it.
Third, we find that even after several rounds of direct instruction and practice, some misconceptions remain. In particular, students do not properly understand how environments chain to get scope right.
Fourth, in a class that had various interventions including interpreters, students did much better than in a class where students learned from interpreters alone. Though we love interpreters and think they have various valuable uses in programming languages education, our results make us question some of the community’s beliefs about the benefits of using interpreters. In particular, some notions of transfer that we would have liked to see do not occur. We therefore believe that the use of interpreters needs much more investigation.
As for the tooling: One of the things we learned from our initial study is that students simply do not have a standardized way of presenting stacks. What goes in them, and how, were all over the map. We conjecture there are many reasons: students mostly see stacks and are rarely asked to draw them; and when they do, they have no standard tools for doing so. So they invent various ad hoc notations, which in turn don’t necessarily reinforce all the aspects that a stack should represent.
We therefore created a small tool for drawing stacks. What we did was repurpose Snap! to create a palette of stack, environment, and heap blocks. It’s important to understand these aren’t runnable programs: these are just static representations of program states. But Snap! is fine with that. This gave us a consistent notation that we could use everywhere: in class, in the textbook, and in homeworks. The ability to make stacks very quickly with drag-and-drop was clearly convenient to students who gained experience with the tool, because many used it voluntarily; it was also a huge benefit for in-class instruction over a more conventional drawing tool. An unexpected success for block syntaxes!
For more details, see the paper.
Student Help-Seeking for (Un)Specified Behaviors
Tags: Education, Misconceptions, Testing, Tools, User Studies
Posted on 02 October 2021.Here’s a summary of the full arc, including later work, of the Examplar project.
Over the years we have done a lot of work on Examplar, our system for helping students understand the problem before they start implementing it. Given that students will even use it voluntarily (perhaps even too much), it would seem to be a success story.
However, a full and fair scientific account of Examplar should also examine where it fails. To that end, we conducted an extensive investigation of all the posts students made on our course help forum for a whole semester, identified which posts had to do with problem specification (and under-specification!), and categorized how helpful or unhelpful Examplar was.
The good news is we saw several cases where Examplar had been directly helpful to students. These should indeed be considered a lower-bound, because the point of Examplar is to “answer” many questions directly, so they would never even make it onto the help forum.
But there is also bad news. To wit:
-
Students sometimes simply fail to use Examplar’s feedback; is this a shortcoming of the UI, of the training, or something inherent to how students interact with such systems?
-
Students tend to overly focus on inputs, which are only a part of the suite of examples.
-
Students do not transfer lessons from earlier assignments to later ones.
-
Students have various preconceptions about problem statements, such as imagining functionality not asked for or constraints not imposed.
-
Students enlarge the specification beyond what was written.
-
Students sometimes just don’t understand Examplar.
These serve to spur future research in this field, and may also point to the limits of automated assistance.
To learn more about this work, and in particular to get the points above fleshed out, see our paper!
Adding Function Transformers to CODAP
Tags: Higher-Order Functions, Education, Tables, Tools
Posted on 22 August 2021.CODAP is a wonderful tool for data transformation. However, it also has important limitations, especially from the perspective of our curricula. So we’ve set about addressing them so that we can incorporate CODAP into our teaching.
CODAP
We at Brown PLT and Bootstrap are big fans of CODAP, a data-analysis tool from the Concord Consortium. CODAP has very pleasant support for working with tables and generating plots, and we often turn to it to perform a quick analysis and generate a graph.
One of the nice things about CODAP, that sets it apart from traditional spreadsheets, is that the basic unit of space is not a table or spreadsheet but a desktop that can contain several objects on it. A workspace can therefore contain many objects side-by-side: a table, a graph, some text, etc.:
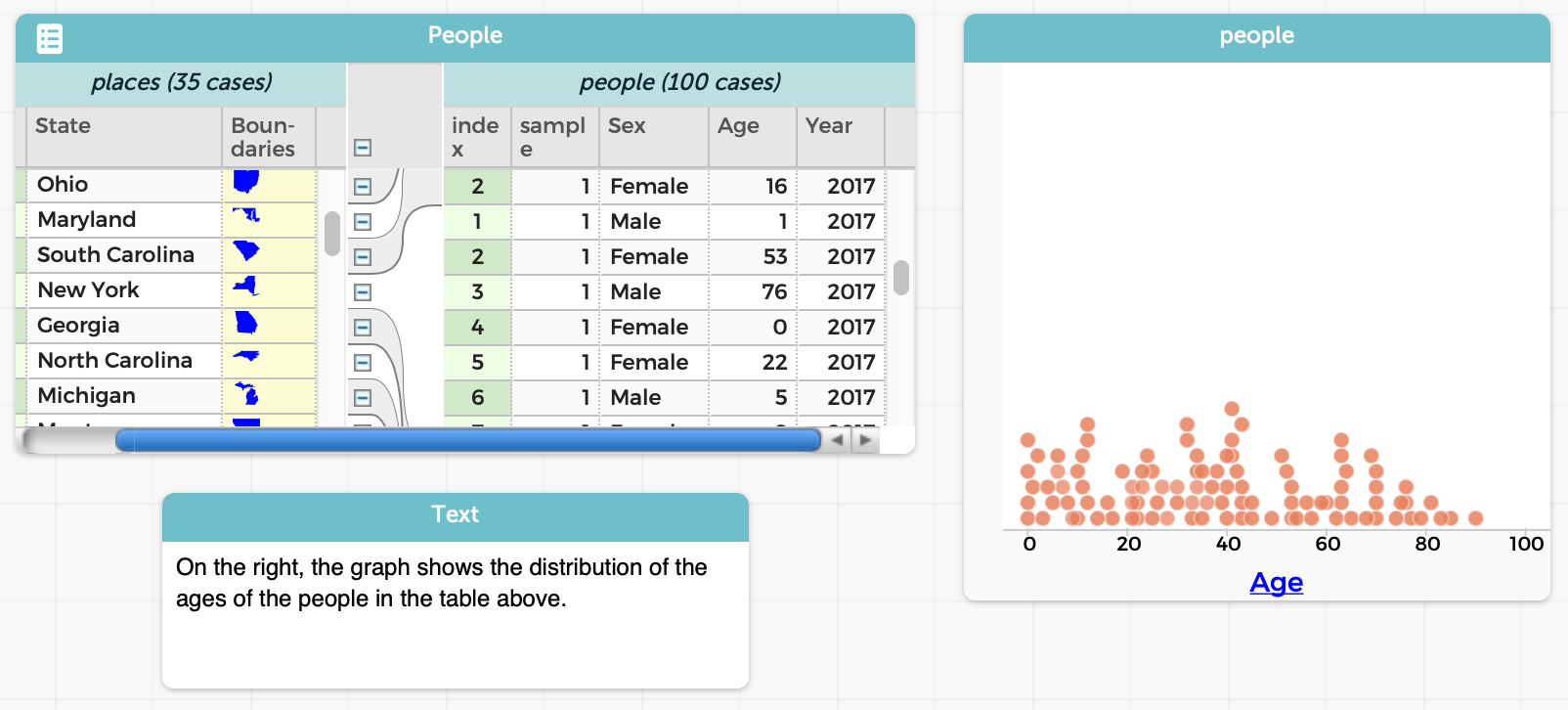
Also, a lot of things in CODAP are done through direct manipulation. This is helpful for younger students, who may struggle with formal programming but can use a GUI to manipulate objects.
There are many other nice features in CODAP, such as the ability to track a data case cross representations, and so on. We urge you to go try it out! When you launch a new CODAP instance, CODAP will offer you a folder of examples, which can help you get acquainted with it and appreciate its features.
What’s Not to Love?
Unfortunately, we don’t love everything about CODAP. We’ll illustrate with an example. To be clear, this is not a bug in CODAP, but rather an important difference of opinion in ease-of-use.
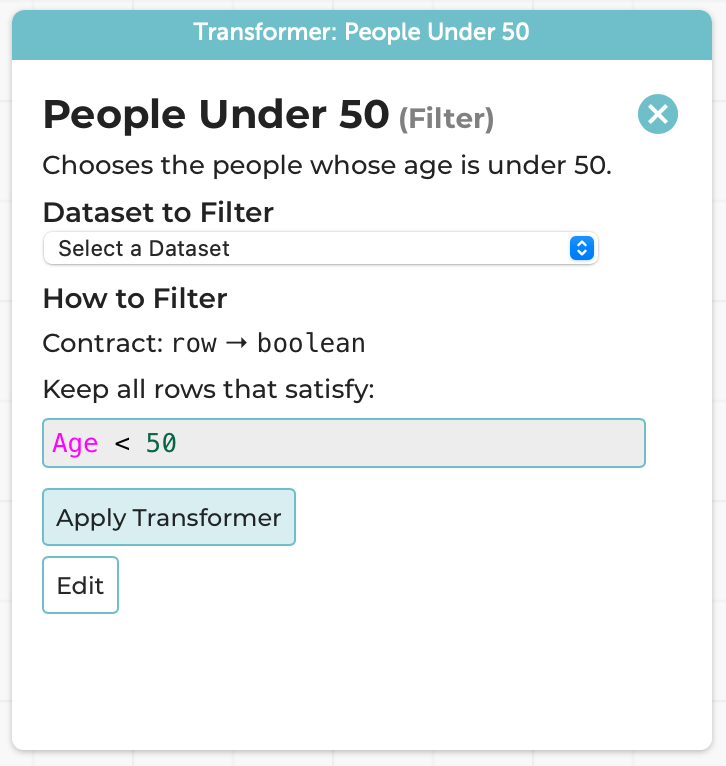
Let’s say we want to find all the people who are below 50 years of age. In CODAP, there are a few ways to do it, all of which have their issues.
If you don’t mind being imprecise (which may be okay for a quick data exploration, but isn’t if you want to, say, compute a statistic over the result):
- Create a new graph.
- Drag the
Agecolumn to the graph. - Select all the items that are under 50 using visual inspection. (Depending on how much data you have and their spread, you’ll quite possibly under- and/or over-shoot.)
- Then do the last few steps below.
If you care to get an accurate selection, instead begin with:
- First, add a new column to the original table.
- Enter a formula for that column (in this case,
Age < 50). - Obtain a selection of the desired items, which can be done in several different ways, also all with trade-offs:
-
Sort by that column. Unfortunately, this won’t work if there’s grouping in the table. You’d have to select manually. (Try it. This may be a bit harder than it seems.)
-
Create a graph as above, but of the new column. This will give you a clean separation into two values. Manually select all the values in the
truecolumn. At least now it will be visually clear if you didn’t select all the right values (if the dataset is not too large). -
Remove the formula for the new column. Now drag it to the leftmost end of the table. (If you don’t remove the formula, you’ll get an error!) Now you have all the elements grouped by
trueandfalse(and operations performed to one can also be performed to the other).
You’re not done! You still have more steps to go:
- If you aren’t already in the table (e.g., if you made a graph), select the table.
- Click on the “Eye” icon.
- Choose the “Set Aside Unselected Cases” entry.
Note that, in most or all of these cases:
- You’ve added a completely superfluous column to your dataset.
- You may have changed the order of items in your dataset.
- You’ve lost the ability to see the original data alongside the filtered data.
- You had to take numerous steps.
- You had to remember to use the Eye icon for filtering, as opposed to other GUI operations for other tasks.
- You had to remember where the Eye icon even is: it’s hidden when a table isn’t selected.
But most of all, in every single case:
- You had to perform all these operations manually.
Why does this matter? We need data science to be reproducible: we should be able to give others our datasets and scripts so they can re-run them to check that they get the same answer, tweak them so they can check the robustness of our answers, and so on. But when all the operations are done manually, there’s no “script”, only output. That focuses on answers rather than processes, and is anti-reproducibility.
In contrast, we think of filtering as a program operation that we apply to a table to produce a new table, leaving the original intact: e.g., the way it works in Pyret. This addresses almost all of the issues above.
Other Pedagogic Consequences
CODAP had to make certain design choices. They made good choices for some settings: for younger children, in particular, the direct manipulation interface works very nicely. It’s a low floor. However, we feel it’s also a lower-than-we’d-like ceiling. There are many things that the CODAP view of data transformation inhibits:
- Making operations explicit, as we noted above.
- Introducing the idea of functions or transformations of data as objects in their own right, not only as manual operations.
- Having explicit data-transformation functions also connects to other related school curricula, such as algebra.
- Saving and naming repeated operations, to learn a bottom-up process of developing abstractions.
- Examining old and new tables side-by-side.
This last point is especially important. A critical task in data science is performing “what if” analyses. What-if fundamentally means we should be able to perform some operation (the “if” part) and compare the output (the “what” part). We might even want to look at multiple different scenarios, representing different possible outcomes. But traditional what-if analysis, whether in CODAP or on spreadsheets, often requires you, the human, to remember what has changed, rather than letting the computer do it for you. (Microsoft Excel has limited support to get around this, but its very presence indicates that spreadsheets, traditionally, did not support what-if analysis—even though that’s how they have often been marketed.)
Finally, there’s also a subtle consequence to CODAP’s design: derived tables must look substantially similar to their parents. In computing terms, the schema should be largely the same. That works fine when an operation has little impact on the schema: filtering doesn’t change the schema at all (in principle, though in CODAP you have to add an extra column…), and adding a new column is a conservative extension. But what if you want to perform an operation that results in a radically different schema? For instance, consider the “pivot wider” and “pivot longer” operations when we create tidy data. The results of those operations have substantially different schemas!
Introducing CODAP Transformers
In response to this critique, we’ve added a new plugin to CODAP called Transformers:
(This work was done by undergrad trio Paul Biberstein, Thomas Castleman, and Jason Chen.)
This introduces a new pane that lists several transformation operations, grouped by functionality:
For instance, with no more textual programming than before (the formula is the same), we can perform our same example as before, i.e., finding all the people younger than 50:
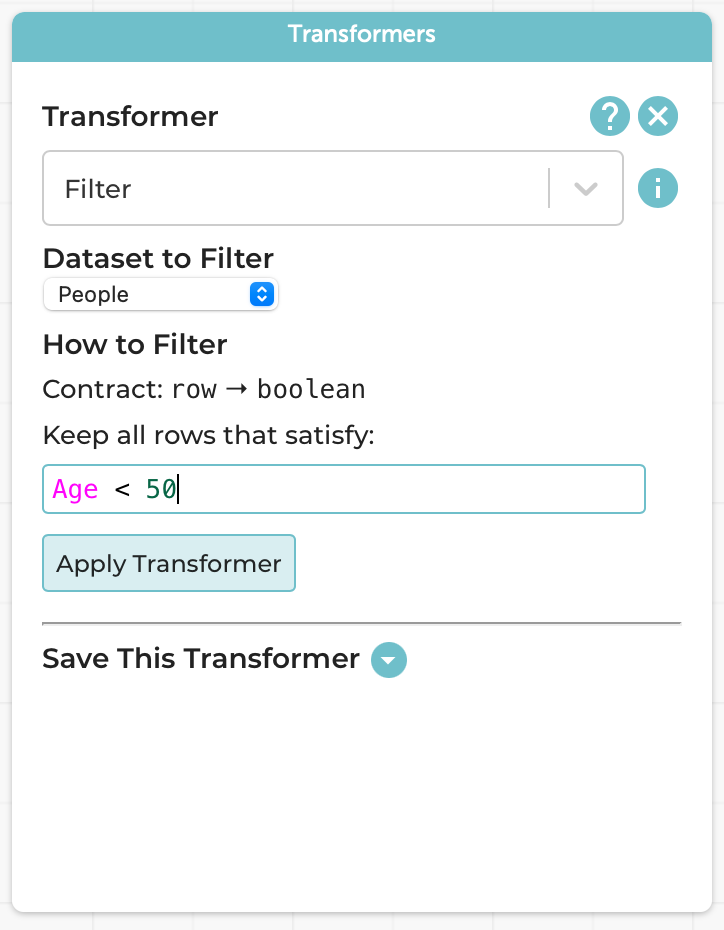
The result is a new table, which co-exists with the original:
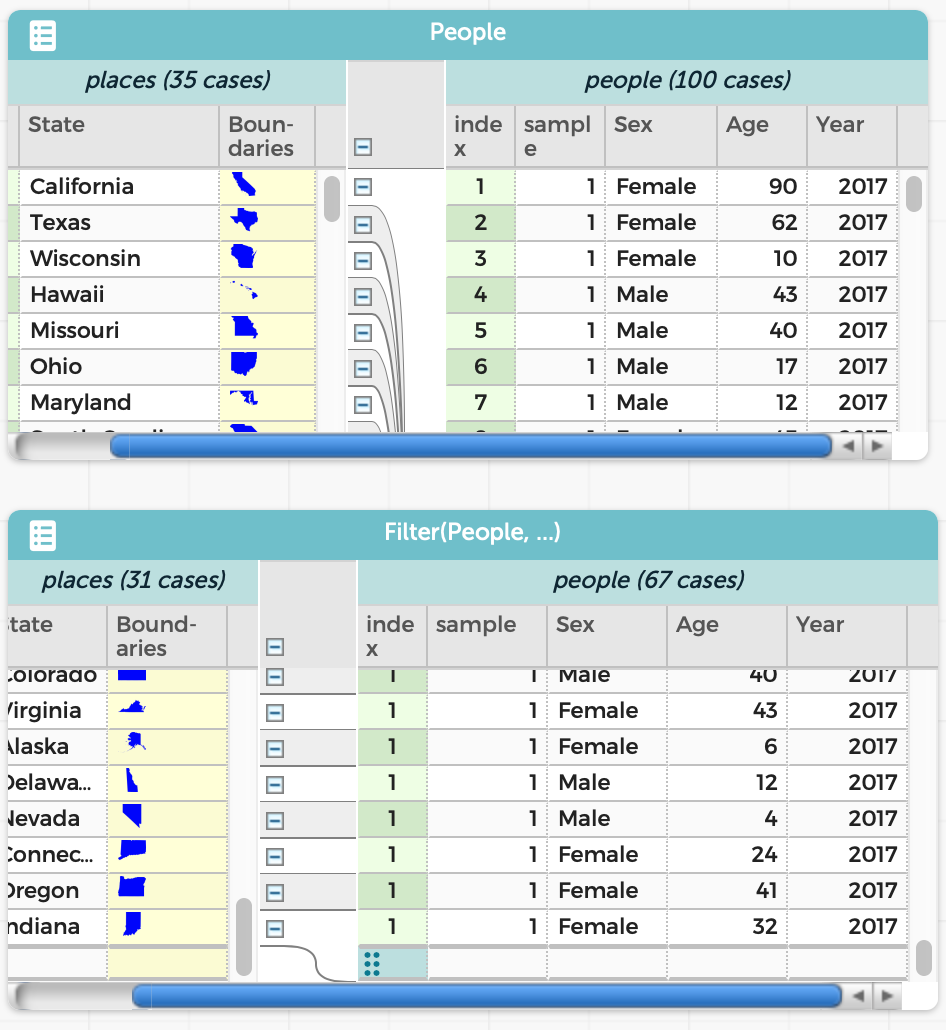
The resulting table is just as much a table as the original. For instance, we can graph the ages in the two tables and see exactly the difference we’d expect:
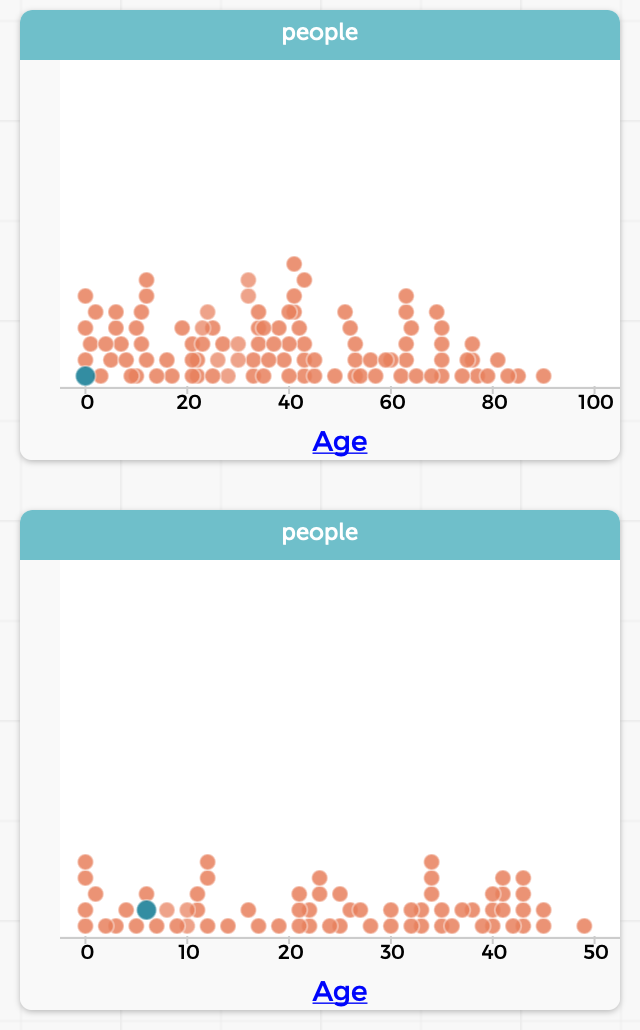
(Over time, of course, you may build up many tables. The Transformers plugin chooses names based on the operations, to make them easy to tell apart. CODAP also lets you resize, minimize, and delete tables. In practice, we don’t expect users to have more than 3–4 tables up at a time.)
Saving Transformers
We might want to perform the same operation on multiple tables. This is valuable in several contexts:
-
We create a hand-curated table, with known answers, as a test case to make sure our operations perform what we expect. After confirming this, we want to be sure that we applied the exact same operation to the real dataset.
-
We want to perform the same operation to several related datasets: e.g., a table per year.
We might also simply want to give a meaningful name to the operation.
In such cases, we can use the “Save This Transformer” option at the bottom of the Transformers pane:
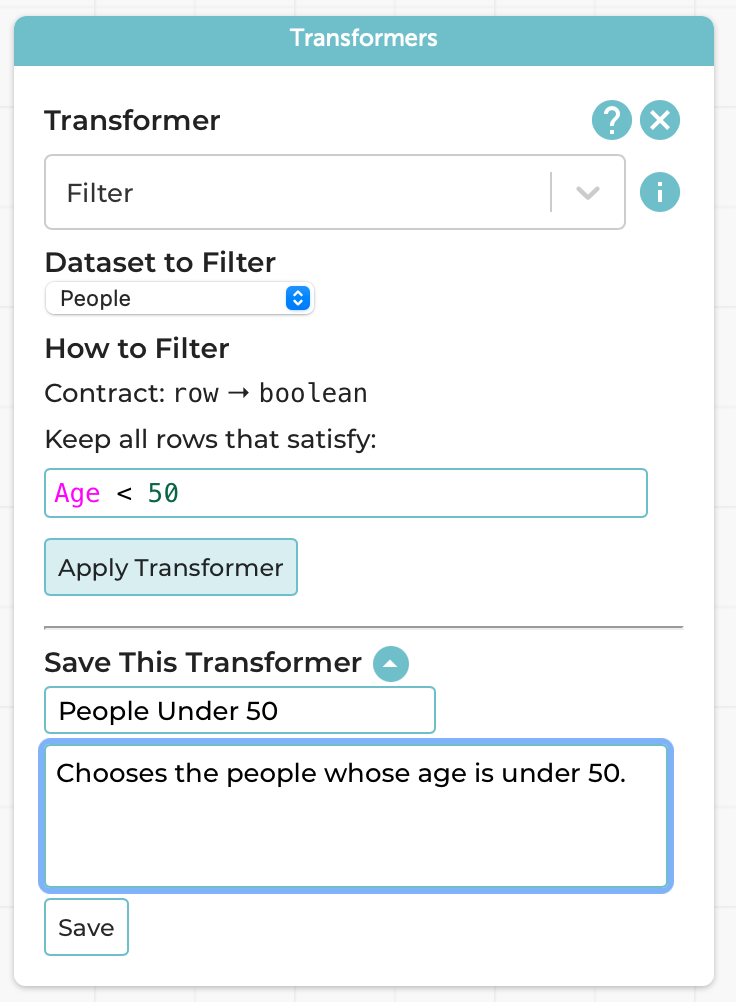
Following the programming processes we follow and teach, we naturally want you to think about the Design Recipe steps when saving it because, in programming terms, you’re creating a new function.
This now creates a new named transformer:
Every part of this is frozen other than the choice of dataset; it can be applied as many times as you want, to as many datasets as you want. The above use-cases are suggestions, but you can use it however you wish.
A Note on Errors
Suppose you try to apply an operation improperly. Say, for instance, you have a table of people that does not have an Age column, and you try to filter people with Age < 50. There are at least two choices that Transformers can take:
-
Allow you to try to perform the operation, and report an error.
-
Prevent you from even trying by simply not showing tables that are invalid in the drop-down list of tables that the operation can be applied to.
We know exactly what the programming languages reader reading this is thinking: “You’re going to choose the latter, right? Right?!? PLEASE TELL ME YOU ARE!!!”
Gentle Reader: we’re not.
Here’s why we chose not to.
- There’s the messy implementation detail of figuring out exactly when a table should or shouldn’t be shown in the drop-down. And we’d have to maintain that across changes to the CODAP language. There are no such problems in the dynamic version.
But hey, we’re language implementors, we can figure these things out. Rather, our real reason comes from human factors:
- Imagine you’re a teacher with a classroom full of students. A student tries to apply an operation to the wrong table. They probably don’t even realize that the operation can’t be applied. All they know is that the table doesn’t appear in the list. Their table doesn’t appear in the list! Their reaction is (perhaps rightly) going to be to raise their hand and say to their teacher, “This tool is broken! It won’t even show me my table!!!” And the teacher, dealing with a whole bunch of students, all in different states, may not immediately realize why the table doesn’t show. Everyone’s frustrated; the student feels stuck, and the teacher may be left feeling inadequate.
In contrast, if we just let the operation happen, here’s what the student sees:

Now the student has a pretty good chance of figuring out for themselves what went wrong: not pulling away the teacher from helping someone else, not blaming the tool, and instead giving themselves a chance of fixing their own problem.
There’s potentially a broader lesson here about making invalid states unrepresentable. Potentially.
Many, Many Transformers!
We’ve focused on just one transformation here. There are many more. We even have the pivoting operations for tidy data! (It would have been wrong to tease you with that up top, otherwise.)
We even take the what-if part seriously: the Compare Transformer lets you compare numeric and categorical data. Believe it or not, the categorical comparison operator was actually inspired by prior work we’ve done for many years on comparing access control policies, router configurations, and SDN programs (see also our two brief position papers). It’s pretty thrilling to see the flow of ideas from security and networking research to data science education in a small but very non-obvious way: the grouping in the categorical output is directly inspired by the multi-terminal decision diagrams of our original Margrave system. For more on this line of work, see our blog post.
Examples
For your benefit, we’ve set up a bunch of pre-built CODAP examples that show you the operations in action:
- Building attributes, Filtering, and Updating data
- Partition
- Filter, Running Sum, and their interaction
- Transformers that produce single values
- Reusing saved transformers
- Categorical Compare
- Numerical Compare
- Pivot operations from tidy data
Make Your Own!
As you might have guessed from the examples above, transformers are now part of the official CODAP tool. You can go play with them right now on the CODAP site. Have fun! Tell us what you learned.
Thanks
Special thanks to our friends at the Concord Consortium, especially William Finzer, Jonathan Sandoe, and Chad Dorsey, for their support.
Developing Behavioral Concepts of Higher-Order Functions
Tags: Higher-Order Functions, Education, User Studies
Posted on 31 July 2021.Higher-Order Functions (HOFs) are an integral part of the programming process. They are so ubiquitous, even Java had to bow and accept them. They’re especially central to cleanly expressing the stages of processing data, as the R community and others have discovered.
How do we teach higher-order functions? In some places, like
How to Design Programs,
HOFs are presented as abstractions over common patterns. That is,
you see a certain pattern of program behavior over and over, and
eventually learn to parameterize it and call it map, filter, and
so on. That is a powerful method.
In this work, we take a different perspective. Our students often write examples first, so they can think in terms of the behavior they want to achieve. Thus, they need to develop an understanding of HOFs as abstractions over common behaviors: “mapping”, “filtering”, etc.
Our goal in this work is to study how well students form behavioral abstractions having been taught code pattern abstractions. Our main instrument is sets of input-output behavior, such as
(list "red" "green" "blue")
-->
(list 3 5 4)
(Hopefully that calls to mind “mapping”.) We very carefully designed a set of these to capture various specific similarities, overlaps, and impossibilities.
We then evaluated students using two main devices, inspired by activities in machine learning:
-
Clustering: Group behaviors into clusters of similar ones.
-
Classification: For each behavior, assign a label.
We also tried labeling over visual presentations.
Our paper describes these instruments in detail, and our outcomes. What is most interesting, perhaps, is not our specific outcomes, but this style of thinking about teaching HOFs. We think the materials—especially the input-output pairs, and a table of properties—will be useful to educators who are tackling this topic. More broadly, we think there’s a huge unexplored space of HOF pedagogy combined with meaningful evaluation. We hope this work inspires more work along these lines.
Adversarial Thinking Early in Post-Secondary Education
Tags: Education, User Studies
Posted on 18 July 2021.Adversarial Thinking (AT) is often described as “thinking like a hacker” or as a “security mindset”. These quasi-definitions are not only problematic in their own right (in some cases, they can be outright circular), they are also too narrow. We believe that AT applies in many other settings as well: in finding ways where machine learning can go wrong, for identifying problems with user interfaces, and for that matter even in software testing and verification.
All these are, however, quite sophisticated computer science concepts. Does that mean AT can only be covered in advanced computer science courses—security, machine learning, formal methods, and the like? Put differently, how much technical sophistication do students need before they can start to engage in it?
We believe AT can be covered starting from a fairly early stage. In this work, we’ve studied its use with (accelerated) introductory post-secondary (university) students. We find that they do very well, but also exhibit some weaknesses. We also find that they are able to reckon with the consequences of systems well beyond their technical capability. Finally, we find that they focus heavily on social issues, not just on technical ones.
In addition to these findings, we have also assembled a rich set of materials covering several aspects of computer science. Students generally found these engaging and thought-provoking, and responded to them with enthusiasm. We think educators would benefit greatly from this collection of materials.
Want to Learn More?
If you’re interested in this, and in the outcomes, please see our paper.
Teaching and Assessing Property-Based Testing
Tags: Education, Formal Methods, Properties, Testing, User Studies
Posted on 10 January 2021.Property-Based Testing (PBT) sees increasing use in industry, but lags significantly behind in education. Many academics have never even heard of it. This isn’t surprising; computing education still hasn’t come to terms with even basic software testing, even when it can address pedagogic problems. So this lag is predictable.
The Problem of Examples
But even people who want to use it often struggle to find good examples of it. Reversing a list drives people to drink, and math examples are hard to relate to. This is a problem from several respects. Without compelling examples, nobody will want to teach it. Even if they do, unless the examples are compelling, students will not pay attention to it. And if the students don’t, they won’t recognize opportunities to use it later in their careers.
This loses much more than a testing technique. We consider PBT a gateway to formal specification. Like a formal spec, it’s an abstract statement about behaviors. Unlike a formal spec, it doesn’t require learning a new language or mathematical formalism, it’s executable, and it produces concrete counter-examples. We therefore use it, in Brown’s Logic for Systems course, as the starting point to more formal specifications. (If they learn nothing about formal specification but simply become better testers, we’d still consider that a win.)
Therefore, for the past 10 years, and with growing emphasis, we’ve been teaching PBT: starting in our accelerated introductory course, then in Logic for Systems, and gradually in other courses as well. But how do we motivate the concept?
Relational Problems
We motivate PBT through what we call relational problems. What are those?
Think about your typical unit test. You write an input-output
pair: f(x) is y. Let’s say it fails:
-
Usually, the function
fis wrong. Congrats, you’ve just caught a bug! -
Sometimes, the test is wrong:
f(x)is not, in fact,y. This can take some reflection, and possibly reveals a misunderstanding of the problem.
That’s usually where the unit-testing story ends. However, there is one more possibility:
- Neither is “wrong”.
f(x)has multiple legal results,w,y, andz; your test chosey, but this particular implementation happened to returnzorwinstead.
We call these “relational” because f is clearly more a relation than
a function.
Some Examples
So far, so abstract. But many problems in computing actually have a relational flavor:
-
Consider computing shortest paths in a graph or network; there can be many shortest paths, not just one. If we write a test to check for one particular path, we could easily run into the problem above.
-
Many other graph algorithms are also relational. There are many legal answers, and the implementation happens to pick just one of them.
-
Non-deterministic data structures inspire relational behavior.
-
Various kinds of matching problems—e.g., the stable-marriage problem—are relational.
-
Combinatorial optimization problems are relational.
-
Even sorting, when done over non-atomic data, is relational.
In short, computing is full of relational problems. While they are not at all the only context in which PBT makes sense, they certainly provide a rich collection of problems that students already study that can be used to expose this idea in a non-trivial setting.
Assessing Student Performance
Okay, so we’ve been having students write PBT for several years now. But how well do they do? How do we go about measuring such a question? (Course grades are far too coarse, and even assignment grades may include various criteria—like code style—that are not strictly germane to this question.) Naturally, their core product is a binary classifier—it labels a purported implementation as valid or invalid—so we could compute precision and recall. However, these measures still fail to offer any semantic insight into how students did and what they missed.
We therefore created a new framework for assessing this. To wit, we took each problem’s abstract property statement (viewed as a formal specification), and sub-divided it into a set of sub-properties whose conjunction is the original property. Each sub-property was then turned into a test suite, which accepted those validators that enforced the property and rejected those that did not. This let us get a more fine-grained understanding of how students did, and what kinds of mistakes they made.
Want to Learn More?
If you’re interested in this, and in the outcomes, please see our paper.
What’s Next?
The results in this paper are interesting but preliminary. Our follow-up work describes limitations to the approach presented here, thereby improving the quality of evaluation, and also innovates in the generation of classifying tests. Check it out!
Students Testing Without Coercion
Tags: Education, Testing, Tools, User Studies
Posted on 20 October 2020.Here’s a summary of the full arc, including later work, of the Examplar project.
It is practically a trope of computing education that students are over-eager to implement, yet woefully under-eager to confirm they understand the problem they are tasked with, or that their implementation matches their expectations. We’ve heard this stereotype couched in various degrees of cynicism, ranging from “students can’t test” to “students won’t test”. We aren’t convinced, and have, for several years now, experimented with nudging students towards early example writing and thorough testing.
We’ve blogged previously about our prototype IDE, Examplar — our experiment in encouraging students to write illustrative examples for their homework assignments before they actually dig into their implementation. Examplar started life as a separate, complementary tool from Pyret’s usual programming environment, providing a buffer just for the purposes of developing a test suite. Clicking Run in Examplar runs the student’s test suite against our implementations (not theirs) and then reports the degree to which the suite was valid and thorough (i.e., good at catching our buggy implementations). With this tool, students could catch their misconceptions before implementing them.
Although usage of this tool was voluntary for all but the first assignment, students relied on it extensively throughout the semester and the quality of final submissions improved drastically compared to prior offerings of the course. Our positive with this prototype encouraged us to fully-integrate Examplar’s feedback into students’ development environment. Examplar’s successor provides a unified environment for the development of both tests and implementation:
This new environment — which provides Examplar-like feedback on every Run — no longer requires that students have the self-awareness to periodically switch to a separate tool. The environment also requires students to first click a “Begin Implementation” button before showing the tab in which they write their implementation.
This unified environment enabled us to study, for the first time, whether students wrote examples early, relative to their implementation progress. We tracked the maximum test thoroughness students had achieved prior to each edit-and-run of their implementations file. Since the IDE notified students of their test thoroughness upon each run, and since students could only increase their thoroughness via edits to their tests file, the mean of these scores summarizes how thoroughly a student explored the problem with tests before fully implementing it.
We find that nearly every student on nearly every assignment achieves some level of thoroughness before their implementation work:

To read more about our design of this environment, its pedagogic context, and our evaluation of students’ development process, check out the full paper here.
Using Design Alternatives to Learn About Data Organizations
Tags: Education, User Studies
Posted on 27 June 2020.A large number of computer science education papers focus on data structures. By this, they mean the canon: lists, queues, stacks, heaps, and so on. These are certainly vital to the design of most programs.
However, there is another kind of “data structure” programmers routinely contend with: how to represent the world your program is about. Suppose, for instance, you’re trying to represent a family’s genealogy. You could:
-
Represent each person as a node and have references to their two biological parents, who in turn have references to their biological parents, and so on. The tree “bottoms out” when we get to people about whom we have no more information.
-
Represent each person as a node and have references to their children instead (a list, say, if we want to preserve their birth order). This tree bottoms out at people who have no children.
-
Represent each coupling as a node, and have references to their children (or issue, as genealogists like to say). Now you may have a kind of node for children and another for coupling.
And so on. There are numerous possibilities. Which one should we pick? It depends on (1) what information we even have, (2) what operations we want to perform, and (3) what complexity we need different operations to take.
Unfortunately, computing education research doesn’t talk about this problem very much at all; in fact, we don’t seem to even have terminology to talk about this issue. In a sense, this is also very much a matter of data structure, though of a different kind: whereas the purely abstract data structures of computer science we might call computational data structures, these — which center around directly representing real-world information — we might instead call representational data structures. That could get pretty confusing, though, so we’ve adopted the term data organization to refer to the latter.
Learning to think about data organization is an essential computing skill. But how early can we teach it? How well can students wrestle with it? What methods should we use? Do they need to be sophisticated programmers before they can engage in reasoning about representations?
Good news: we can begin this quite early, and students don’t need to be sophisticated computer scientists: they can just think about the world, and their experiences living in it, to reason about data organizations. Representational data structures probably do a far better job of drawing on their lived experience than computational ones do! (Unless they’ve previously lived as a computer.)
There are several ways we could introduce this topic. We chose to expose them to pairs of representations for the same domain, and have them compare the two. This is related to theories of perception. Read the paper to learn more!
Somewhat subtly, this also adds a dimension to “computational thinking” that is usually quite missing from standard discussions about it. Activities like those described in this paper generate new and engaging activities that many students can participate in. Indeed, computing background does not seem to matter much in our data, and a more diverse group of students is likely to make a much richer set of judgments—thereby enabling students in traditionally underrepresented groups to contribute based on their unique experiences, and also feel more valued.
What Help Do Students Seek in TA Office Hours?
Tags: Education, User Studies
Posted on 20 May 2020.In computer science, a large number of students get help from teaching assistants (TAs). A great deal of their real education happens in these hours. While TA hours are an excellent resource, they are also rather opaque to the instructors, who do not really know what happens in them.
How do we construct a mechanism to study what happens in hours? It’s actually not obvious at all:
-
We could set up cameras to record all the interactions in hours. While this would provide a lot of information, it significantly changes the nature of hours. For many students, hours are private time with a TA, where they can freely speak about their discomfort and get help from a peer; they might ask personal questions; they might also complain about the instructor. One does not install cameras in confessionals.
-
We could ask TAs to write extensive notes (redacting private information) after the student has left. This also has various flaws:
-
Their memory may be faulty.
-
Their recollection may be biased by their own beliefs.
-
It would slow down processing students, who already confront overly-long lines and waits.
-
What do we instead want? A process that is non-intrusive, lightweight, and yet informative. We have to also give up on perfect knowledge, and focus on information that is actually useful to the instructor.
Part of the problem is that we as a community lack a systematic method to help students in the first place. If students have no structure to how they approach help-seeking, then it’s hard to find patterns and make sense of what they actually do.
However, this is exactly a problem that the How to Design Programs Design Recipe was addressed to solve. It provides a systematic way for students to structure their problem-solving and help-seeking. TAs are instructed to focus on the steps of the Design Recipe in order, not addressing later steps until students have successfully completed the earlier ones. This provides an “early warning” diagnostic, addressing root causes rather than their (far-removed) manifestations.
Therefore, we decided to use the Design Recipe steps as a lens for obtaining insight into TA hours. We argue that this provides a preliminary tool that addresses our needs: it is lightweight, non-intrusive, and yet useful to the instructor. Read the paper to learn more!
Combating Misconceptions by Encouraging Example-Writing
Tags: Education, Misconceptions, Testing, Tools
Posted on 11 January 2020.Here’s a summary of the full arc, including later work, of the Examplar project.
When faced with an unfamiliar programming problem, undergraduate computer science students all-too-often begin their implementations with an incomplete understanding of what the problem is asking, and may not realize until far into their development process (if at all) that they have solved the wrong problem. At best, a student realizes their mistake, suffers from some frustration, and is able to correct it before the final submission deadline. At worst, they might not realize their mistake until they receive feedback on their final submission—depriving them of the intended learning goal of the assignment.
Educators must therefore provide students with some mechanism by which students can evaluate their own understanding of a problem—before they waste time implementing some misconceived variation of that problem. To this end, we provide students with Examplar: an IDE for writing input–output examples that provides on-demand feedback on whether the examples are:
- valid (consistent with the problem), and
- thorough (explore the conceptually interesting corners of the problem).
For a demonstration, watch this brief video!
With its gamification, we believed students would find Examplar compelling to use. Moreover, we believed its feedback would be helpful. Both of these hypotheses were confirmed. We found that students used Examplar extensively—even when they were not required to use it, and even for assignments for which they were not required to submit test cases. The quality of students’ final submissions generally improved over previous years, too. For more information, read the full paper here!
The Hidden Perils of Automated Assessment
Posted on 26 July 2018.
We routinely rely on automated assessment to evaluate our students’ work on programming assignments. In principle, these techniques improve the scalability and reproducibility of our assessments. In actuality, these techniques may make it incredibly easy to perform flawed assessments at scale, with virtually no feedback to warn the instructor. Not only does this affect students, it can also affect the reliability of research that uses it (e.g., that correlates against assessment scores).
To Test a Test Suite
The initial object of our study was simply to evaluate the quality of student test suites. However, as we began to perform our measurements, we wondered how stable they were, and started to use different methods to evaluate stability.
In this group, we take the perspective that test suites are classifiers of implementations. You give a test suite an implementation, and it either accepts or rejects it. Therefore, to measure the quality of a test suite, we can standard metrics for classifiers, true positive rate and true negative rate. However, to actually do this, we need a set of implementations that we know, a priori, to be correct or faulty.
| Ground Truth | |||
|---|---|---|---|
| Correct | Faulty | ||
| Test Suite |
Accept | True Negative | False Negative |
| Reject | False Positive | True Positive | |
A robust assessment of a classifier may require a larger collection of known-correct and known-faulty implementations than the instructor could craft themselves. Additionally, we can leverage all of the implementations that students are submitting—we just need to determine which are correct and which are faulty.
There are basically two ways of doing this in the literature; let’s see how they fare.
The Axiomatic Model
In the first method, the instructor writes a test suite and whatever that test suite’s judgments is used as the ground truth; e.g., if the instructor test suite accepts a given implementation, it is a false positive for a student’s test suite to reject it.
The Algorithmic Model
The second method does this by taking every test suite you have (i.e., both the instructor’s and the students’), running them all against a known-correct implementation, and gluing all the ones that pass it into one big mega test suite that is used to establish ground truth.
A Tale of Two Assessments
We applied each model in turn to classify 38 student implementations and a handful of specially crafted ones (both correct and faulty, in case the student submissions were skewed heavily towards faultiness or correctness), then computed the true-positive and true-negative rate for each student’s test suite.
The choice of underlying implementation classification model substantially impacted the apparent quality of student test suites. Visualized as kernel density estimation plots (akin to smoothed histograms):
The Axiomatic Model:

The Algorithmic Model:
Judging by this plot, students performed astoundingly poorly at detecting buggy implementations, but quite well at identifying correct ones.
Towards Robust Assessments
So which is it? Do students miss half of all buggy implementations, or are they actually astoundingly good? In actuality: neither. These strikingly divergent analysis outcomes are produced by fundamental, theoretical flaws in how these models classify implementations.
We were alarmed to find that these theoretical flaws, to varying degrees, affected the assessments of every assignment we evaluated. Neither model provides any indication to warn instructors when these flaws are impacting their assessments. For more information about these perils, see our paper, in which we present a technique for instructors and researchers that detects and protects against them.
Mystery Languages
Tags: Education, Programming Languages, Semantics
Posted on 05 July 2018.How do you learn a new language? Do you simply read its reference manual, and then you’re good to go? Or do you also explore the language, trying things out by hand to see how they behave?
This skill—learning about something by poking at it—is frequently used but almost never taught. However, we have tried to teach it via what we dub mystery languages, and this post is about how we went about it.
Mystery Lanuages
A mystery language is exactly what it sounds like: a programming language whose behavior is a mystery. Each assignment comes with some vague documentation, and an editor in which you can write programs. However, when you run a program it will produce multiple answers! This is because there are actually multiple languages, with the same syntax but different semantics. The answers you get are the results of running your program in all of the different languages. The goal of the assignment is to find programs that tell the languages apart.
As an example, maybe the languages have the syntax a[i], and the
documentation says that this “accesses an array a at index i”.
That totally specifies the behavior of this syntax, right?
Not even close. For example, what happens if the index is out of bounds?
Does it raise an error (like Java), or return undefined (like
JavaScript), or produce nonsense (like C), or wrap the index to a
valid one (like Python)? And what happens if the index is 2.5, or
"2", or 2.0, or "two"?
(EDIT: Specifically, Python wraps negative indices that are smaller than the length of the array.)
Students engage with the mystery languages in three ways:
- The first part of each assignment is to find a set of programs that distinguishes the different languages (a.k.a. a classifier).
- The second part of the assignment is to describe a theory that explains the different behaviors of the languages. (For example, a theory about C’s behavior could include accessing heap addresses past the end of an array.)
- Finally, after an assignment is due, there’s an in-class discussion and explanation of the mystery languages. This is especially useful to provide terminology for behaviors that students encountered in the languages.
This example is somewhat superficial (the real mystery languages mostly use more significant features than array access), but you get the idea: every aspect of a programming language comes with many possible designs, and the mystery languages have students explore them first-hand.
Why Mystery Languages?
We hope to teach a number of skills through mystery languages:
- Evaluating Design Decisions: The mystery languages are almost entirely based on designs chosen by real languages: either historical choices that have since been settled, or choices that are still up in the air and vary between modern languages. Students get to explore the consequences of these decisions themselves, so that they get a feel for them. And the next day in class they learn about the broader historical context.
- Syntax vs. Semantics: We are frustrated by how frequently discussions about programming languages revolve around syntax. With luck, showing students first-hand that a single syntax can have a variety of semantics will bring their discussions to a somewhat higher level.
- Adversarial Thinking: Notice that the array example was all about exploring edge cases. If you only ever wrote correct, safe, boring programs then you’d never notice the different ways that array access could work. This is very similar to the kind of thinking you need to do when reasoning about security, and we hope that students might pick up on this mindset.
- Experimental Thinking: In each assignment, students are asked not only to find programs that behave differently across the mystery languages, but also to explain the behavior of the different languages. This is essentially a scientific task: brainstorm hypotheses about how the languages might work; experimentally test these hypotheses by running programs; discard any hypothesis that was falsified; and iterate.
Adopting Mystery Languages
If you want to use Mystery Languages in your course, email us and we’ll help you get started!
There are currently 13 mystery languages, and more in development. At Brown, we structured our programming languages course around these mystery languages: about half of the assignments and half of the lectures were about mystery languages. However, mystery languages are quite flexible, and could also be used as a smaller supplement to an existing course. One possibility is to begin with one or two simpler languages to allow students to learn how they work, and from there mix and match any of the more advanced languages. Alternatively, you could do just one or two mystery languages to meet specific course objectives.
Learn More
You can learn more about mystery languages in our SNAPL’17 paper. For the latest version of the software, see this repository.
The Pyret Programming Language: Why Pyret?
Tags: Education, Programming Languages, Pyret, Semantics, Types
Posted on 26 June 2016.We need better languages for introductory computing. A good introductory language makes good compromises between expressiveness and performance, and between simplicity and feature-richness. Pyret is our evolving experiment in this space.
Since we expect our answer to this question will evolve over time, we’ve picked a place for our case for the language to live, and will update it over time:
The Pyret Code; or A Rationale for The Pyret Programming Language
The first version answers a few questions that we expect many people have when considering languages in general and languages for education in particular:
- Why not just use Java, Python, Racket, OCaml, or Haskell?
- Will Pyret ever be a full-fledged programming language?
- But there are lots of kinds of “education”!
- What are some ways the educational philosophy influences the langauge?
In this post, it’s worth answering one more immediate question:
What’s going on right now, and what’s next?
We are currently hard at work on three very important features:
-
Support for static typing. Pyret will have a conventional type system with tagged unions and a type checker, resulting in straightforward type errors without the complications associated with type inference algorithms. We have carefully designed Pyret to always be typeable, but our earlier type systems were not good enough. We’re pretty happy with how this one is going.
-
Tables are a critical type for storing real-world data. Pyret is adding linguistic and library support for working effectively with tables, which PAPL will use to expose students to “database” thinking from early on.
-
Our model for interactive computation is based on the “world” model. We are currently revising and updating it in a few ways that will help it better serve our new educational programs.
On the educational side, Pyret is already used by the Bootstrap project. We are now developing three new curricula for Bootstrap:
-
A CS1 curriculum, corresponding to a standard introduction to computer science, but with several twists based on our pedagogy and materials.
-
A CS Principles curriculum, for the new US College Board Advanced Placement exam.
-
A physics/modeling curriculum, to help teach students physics and modeling through the medium of programming.
If you’d like to stay abreast of our developments or get involved in our discussions, please come on board!
In-flow Peer Review: An Overview
Tags: Education, In-Flow Peer Review
Posted on 02 January 2016.We ought to give students opportunities to practice code review. It’s a fundamental part of modern software development, and communicating clearly and precisely about code is a skill that only develops with time. It also helps shape software projects for the better early on, as discussions about design and direction in the beginning can avoid costly mistakes that need to be undone later.
Introducing code review into a curriculum faces a few challenges. First, there is the question of the pedagogy of code review: what code artifacts are students qualified to review? Reviewing entire solutions may be daunting if students are already struggling to complete their own, and it can be difficult to scope feedback for an entire program. Adding review also introduces a time cost for assignments, if it actually makes up a logically separate assignment from the code under review.
We propose in-flow peer review (IFPR) as a strategy for blending some of these constraints and goals. The fundamental idea is to break assignments into separately-submittable chunks, where each intermediate submittable is designed to be amenable to a brief peer review. The goal is for students to practice review, benefit from the feedback they get from their peers while the assignment is still ongoing, and also learn from seeing other approaches to the same problem. We’ve experimented with in-flow peer review in several settings, and future posts will discuss more of our detailed results. Here, we lay out some of the design space of in-flow peer review, including which intermediate steps might show promise, and what other choices a practitioner of IFPR can make. This discussion is based on our experience and on an ITiCSE working group report that explored many of the design dimensions of IFPR. That report has deeper discussions of the topics we introduce here, along with many other design dimensions and examples for IFPR.
What to Submit
The first question we need to address is what pieces of assignments are usefully separable and reviewable. There are a number of factors at work here. For example, it may be detrimental from an evaluation point of view to share too much of a solution while the assignment is ongoing, so the intermediate steps shouldn’t “give away” the whole solution. The intermediate steps need to be small enough to review in a brief time window, but interesting enough to prompt useful feedback. Some examples of intermediate steps are:
- Full test suites for the problem, without the associated solution
- A class or structure definition used to represent a data structure, without the associated operations
- Function headers for helper functions without the associated body
- Full helper functions, without the associated “main” implementation
- A task-level breakdown of a work plan for a project (e.g. interface boundaries, test plan, and class layout)
- A description of properties (expressed as predicates in a programming language, or informally) that ought to be true of an eventual implementation
Each of these reviewable artifacts can give students hints about a piece of the problem without giving away full solutions, and seem capable of prompting meaningful feedback that will inform later stages of the assignment.
How to Review
The second question has to do with the mechanics of review itself. How many submissions should students review (and how many reviews should they receive)? Should students’ names be attached to their submissions and/or their reviews, or should the process be completely anonymous? What prompts should be given in the review rubric to guide students towards giving useful feedback? How much time should students have to complete reviews, and when should they be scheduled in the assignment process?
These questions, obviously, don’t have right or wrong answers, but some in particular are useful to discuss, especially with respect to different goals for different classrooms.
- Anonymity is an interesting choice. Professional code review is seldom anonymous, and having students take ownership of their work encourages an attitude of professionalism. If reviewer-reviewee pairs can identify one another, they can communicate outside the peer review system, as well, which may be encouraged or not desired depending on the course. Anonymity has a number of benefits, in that it avoids any unconscious bias in reviews based on knowing another student’s identity, and may make students feel more comfortable with the process.
- Rubric design can heavily shape the kinds of reviews students write. At one extreme, students could simply get an empty text box and provide only free-form comments. Students could also be asked to identify specific features in their review (“does the test suite cover the case of a list with duplicate elements?”), fill in line-by-line comments about each part of the submission, write test cases to demonstrate bugs that they find, or many other structured types of feedback. This is a pretty wide-open design space, and the complexity and structure of the rubric can depend on curricular goals, and on the expected time students should take for peer review.
- Scheduling reviews and intermediate submissions is an interesting balancing act. For a week-long assignment, it may be useful to have initial artifacts submitted as early as the second day, with reviews submitted on the third day, in order to give students time to integrate the feedback into their submissions. For longer assignments, the schedule can be stretched or involve more steps. This can have ancillary benefits, in that students are forced to start their assignment early in order to participate in the review process (which can be mandatory), combatting procrastination.
Logistics (and Software Support)
Setting up an IFPR workflow manually would involve serious instructor effort, so software support is a must for an easy integration of IFPR into the classroom. The software ought to support different review workflows and rubrics, across various assignment durations in types, in order to be useful in more than one class or setting. In the next post, we’ll talk about some design goals for IFPR software and how we’ve addressed them.
CS Student Work/Sleep Habits Revealed As Possibly Dangerously Normal
Tags: Education, User Studies
Posted on 14 June 2014. Written by Jesse Polhemus, and originally posted at the Brown CS blogImagine a first-year computer science concentrator (let’s call him Luis) e-mailing friends and family back home after a few weeks with Brown Computer Science (BrownCS). Everything he expected to be challenging is even tougher than anticipated: generative recursion, writing specifications instead of implementations, learning how to test his code instead of just writing it. Worst of all is the workload. On any given night, he’s averaging –this seems too cruel to be possible– no more than eight or nine hours of sleep.
Wait, what? Everyone knows that CS students don't get any sleep, so eight or nine hours is out of the question. Or is it? Recent findings from PhD student Joseph Gibbs Politz, adjunct professor Kathi Fisler, and professor Shriram Krishnamurthi analyze when students completed tasks in two different BrownCS classes, shedding interesting light on an age-old question: when do our students work, and when (if ever) do they sleep? The question calls to mind a popular conception of the computer scientist that Luis has likely seen in countless movies and books:
- Hours are late. (A recent poster to boardgames@lists.cs.brown.edu requests a 2 PM start time in order to avoid being “ridiculously early” for prospective players.)
- Sleep is minimal. BrownCS alumnus Andy Hertzfeld, writing about the early days of Apple Computer in Revolution in the Valley, describes the “gigantic bag of chocolate-covered espresso beans” and “medicinal quantities of caffeinated beverages” that allowed days of uninterrupted coding.
Part 1: Deadline Experiments
The story begins a few years before Luis’s arrival, when Shriram would routinely schedule his assignments to be due at the 11:00 AM start of class. “Students looked exhausted,” he remembers. “They were clearly staying up all night in order to complete the assignment just prior to class.”
Initially, he moved the deadline to 2:00 AM, figuring that night owl students would finish work in the early hours of the morning and then get some sleep. This was effective, but someone pointed out that it was unfair to other professors who taught earlier classes and were forced to deal with tired students who had finished Shriram’s assignment but not slept sufficiently.
“My final step,” he explains, “was to change deadlines to midnight. I also began penalizing late assignments on a 24-hour basis instead of an hourly one. This encourages students to get a full night’s sleep even if they miss a deadline.”
This was the situation when Luis arrives. The next task was to start measuring the results.
Part 2: Tracking Events
Shriram, Kathi, and Joe analyzed two of Shriram’s classes, CS 019 and CS 1730. For each class, Luis must submit test suites at any time he chooses, then read reviews of his work from fellow students. He then continues working on the solution, eventually producing a final implementation that must be submitted prior to the midnight deadline.
Part 3: Reality And Mythology
Given these parameters, what work and sleep patterns would you expect? We asked professor Tom Doeppner to reflect on Luis and share his experience of working closely with students as Director of Undergraduate Studies and Director of the Master’s Program. “Do students work late? I know I get e-mail from students at all hours of the night,” he says, “and I found out quickly that morning classes are unpopular, which is why I teach in the afternoon. Maybe it’s associated with age? I liked to work late when I was young, but I got out of the habit in my thirties.”
Asked about the possible mythologizing of late nights and sleeplessness, Tom tells a story from his own teaching: “Before we broke up CS 169 into two classes, the students had t-shirts made: ‘CS 169: Because There Are Only 168 Hours In A Week’. I think there’s definitely a widespread belief that you’re not really working hard unless you’re pulling multiple all-nighters.”
This doesn’t exactly sound like Luis’s sleep habits! Take a look at the graphs below to see how mythology and reality compare.
Part 4: Results And Conclusions
The graphs below depict test suite submissions, with time displayed in six-hour segments. For example, between 6 PM and the midnight deadline (“6-M”), 50 CS 173 students are submitting tests.
This graph is hypothetical, showing Joe, Kathi, and Shriram’s expectations for submission activity. They expected activity to be slow and increase steadily, culminating in frantic late-night activity just before the deadline. Generally taller “M-6” (midnight to 6 AM) bars indicate late-night work and a corresponding flurry of submissions, followed by generally shorter “6-N” (6 AM to noon) bars when students tried to get a few winks in. Cumulatively, these two trends depict the popular conception of the computer science student who favors late hours and perpetually lacks sleep.
These graphs show actual submissions. As expected, activity generally increases over time and the last day contains the majority of submissions. However, unexpectedly, the “N-6” (noon to 6 PM) and “6-M” (6 PM to midnight) segments are universally the most active. In the case of the CS 173 graph, this morning segment contains far more submissions than any other of the day’s three segments. In both of these graphs, the “M-6” (midnight to 6 AM) segments are universally the least active, even the day the assignment is due. For example, the final segment of this type, which represents the last available span of early morning hours, is among the lowest of all segments, with only ten submissions occurring. In contrast, the corresponding “6-N” (6 AM to noon) shows more than four times as many submissions, suggesting that most students do their work before or after the pre-dawn hours but not during them.
“I wouldn’t have expected that,” Joe comments. “I think of the stories folks tell of when they work not lining up with that, in terms of staying up late and getting up just in time for class. Our students have something important to do at midnight other than work: they cut off their work before midnight and do something else. For the majority it’s probably sleep, but it could just be social time or other coursework. Either way, it’s an interesting across-the-board behavior.”
If word of these results gets out, what can Luis and his fellow students expect? “People will realize,” Shriram says, “that despite what everyone likes to claim, students even in challenging courses really are getting sleep, so it’s okay for them to, too.” Joe agrees: “There isn’t so much work in CS that you have to sacrifice normal sleeping hours for it.”
Luis, his family, and his well-rested classmates will undoubtedly be glad to hear it. The only question is: will their own descriptions of their work/sleep habits change to match reality, or are tales of hyper-caffeinated heroics too tempting to resist?
Appendix
The graphs above are simplified for readability, and aggregated into 6-hour increments. Below we include graphs of the raw data in 3-hour increments. This shows that there is some work going on from 12am-3am the night before assignments are due, but essentially nothing from 3am-6am.
In both of these classes, we were also performing experiments on code review, so the raw data includes when students read the code reviews they received, in addition to when they submitted their work. Since the review necessarily happens after submission, and the reading of the review after that, we see many more “late” events for reading reviews.
CS019 in 3-hour increments:
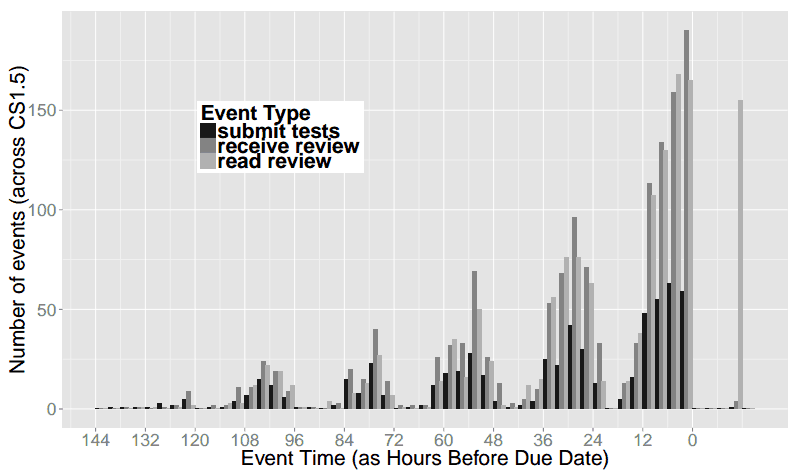
CS173 in 3-hour increments:
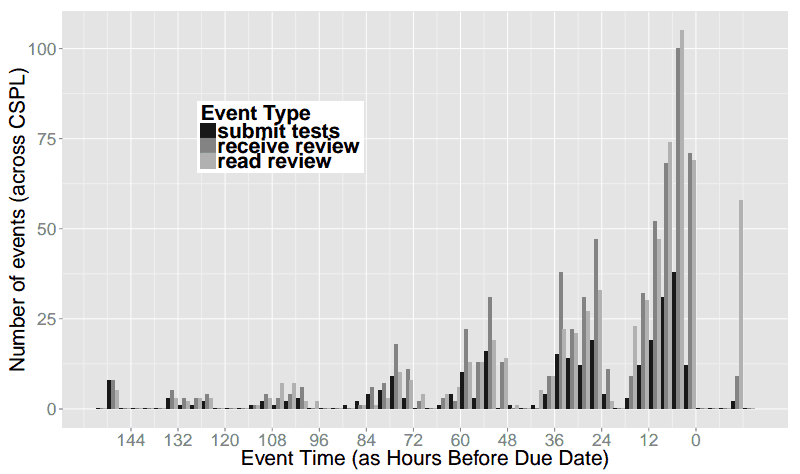
From MOOC Students to Researchers
Tags: Education, Programming Languages, Semantics
Posted on 18 June 2013.Much has been written about MOOCs, including the potential for its users to be treated, in effect, as research subjects: with tens of thousands of users, patterns in their behavior will stand out starkly with statistical significance. Much less has been written about using MOOC participants as researchers themselves. This is the experiment we ran last fall, successfully.
Our goal was to construct a “tested semantics” for Python, a popular programming language. This requires some explanation. A semantics is a formal description of the behavior of a language so that, given any program, a user can precisely predict what the program is going to do. A “tested” semantics is one that is validated by checking it against real implementations of the language itself (such as the ones that run on your computer).
Constructing a tested semantics requires covering all of a large language, carefully translating its every detail into a small core language. Sometimes, a feature can be difficult to translate. Usually, this just requires additional quantities of patience, creativity, or elbow grease; in rare instances, it may require extending the core language. Doing this for a whole real-world language is thus a back-breaking effort.
Our group has had some success building such semantics for multiple languages and systems. In particular, our semantics for JavaScript has come to be used widely. The degree of interest and rapidity of uptake of that work made clear that there was interest in this style of semantics for other languages, too. Python, which is not only popular but also large and complex (much more so than JavaScript), therefore seemed like an obvious next target. However, whereas the first JavaScript effort (for version 3 of the language) took a few months for a PhD student and an undergrad, the second one (focusing primarily on the strict-mode of version 5) took far more effort (a post-doc, two PhD students, and a master's student). JavaScript 5 approaches, but still doesn't match, the complexity of Python. So the degree of resources we would need seemed daunting.
Crowdsourcing such an effort through, say, Mechanical Turk did not seem very feasible (though we encourage someone else to try!). Rather, we needed a trained workforce with some familiarity with the activity of formally defining a programming language. In some sense, Duolingo has a similar problem: to be able to translate documents it needs people who know languages. Duolingo addresses it by...teaching languages! In a similar vein, our MOOC on programming languages was going to serve the same purpose. The MOOC would deliver a large and talented workforce; if we could motivate them, we could then harness them to help perform the research.
During the semester, we therefore gave three assignments to get students warmed up on Python: 1, 2, and 3. By the end of these three assignments, all students in the class had had some experience wrestling with the behavior of a real (and messy) programming language, writing a definitional interpreter for its core, desugaring the language to this core, and testing this desugaring against (excerpts of) real test suites. The set of features was chosen carefully to be both representative and attainable within the time of the course.
(To be clear, we didn't assign these projects only because we were interested in building a Python semantics. We felt there would be genuine value for our students in wrestling with these assignments. In retrospect, however, this was too much work, and it interfered with other pedagogic aspects of the course. As a result, we're planning to shift this workload to a separate, half-course on implementing languages.)
Once the semester was over, we were ready for the real business to begin. Based on the final solutions, we invited several students (out of a much larger population of talent) to participate in taking the project from this toy sub-language to the whole Python language. We eventually ended up with an equal number of people who were Brown students and who were from outside Brown. The three Brown students were undergraduates; the three outsiders were an undergraduate student, a professional programmer, and a retired IT professional who now does triathlons. The three outsiders were from Argentina, China, and India. The project was overseen by a Brown CS PhD student.
Even with this talented workforce, and the prior preparation done through the course and creating the assignments prepared for the course, getting the semantics to a reasonable state was a daunting task. It is clear to us that it would have been impossible to produce an equivalent quality artifact—or to even come close—without this many people participating. As such, we feel our strategy of using the MOOC was vindicated. The resulting paper has just been accepted at a prestigious venue that was the most appropriate one for this kind of work, with eight authors: the lead PhD student, the three Brown undergrads, the three non-Brown people, and the professor.
A natural question is whether making the team even larger would have helped. As we know from Fred Brooks's classic The Mythical Man Month, adding people to projects can often hurt rather than help. Therefore, the determinant is to what extent the work can be truly parallelized. Creating a tested semantics, as we did, has a fair bit of parallelism, but we may have been reaching its limits. Other tasks that have previously been crowdsourced—such as looking for stellar phenomena or trying to fold proteins—are, as the colloquial phrase has it, “embarrassingly parallel”. Most real research problems are unlikely to have this property.
In short, the participants of a MOOC don't only need to be thought of as passive students. With the right training and motivation, they can become equal members of a distributed research group, one that might even have staying power over time. Also, participation in such a project can help a person establish their research abilities even when they are at some remove from a research center. Indeed, the foreign undergraduate in our project will be coming to Brown as a master's student in the fall!
Would we do it again? For this fall, we discussed repeating the experiment, and indeed considered ways of restructuring the course to better support this goal. But before we do, we have decided to try to use machine learning instead. Once again, machines may put people out of work.
The New MOOR's Law
Posted on 01 April 2013.
Though this was posted on April 1, and the quotes in this article should be interpreted relative to that date, MOOR itself is not a joke. Students from our online course produced a semantics for Python, with a paper describing it published at OOPSLA 2013.
PROVIDENCE, RI, USA - With the advent of Massively Open and Online Courses (MOOCs), higher education faces a number of challenges. Services like Udacity and Coursera will provide learning services of equivalent quality for a fraction of the cost, and may render the need for traditional education institutions obsolete. With the majority of universities receiving much of their cash from undergraduate tuition, this makes the future of academic research uncertain as well.
"[Brown]
lacks the endowment of a school like Harvard to weather the coming
storm."
-Roberto Tamassia
Schools may eventually adapt, but it's unclear what will happen to research programs in the interim. “I'm concerned for the future of my department at Brown University, which lacks the endowment of a school like Harvard to weather the coming storm,” said Roberto Tamassia, chair of the Computer Science department at Brown.
But one Brown professor believes he has a solution for keeping his research program alive through the impending collapse of higher education. He calls it MOOR: Massively Open and Online Research. The professor, Shriram Krishnamurthi, claims that MOOR can be researchers' answer to MOOCs: “We've seen great user studies come out of crowdsourcing platforms like Mechanical Turk. MOOR will do the same for more technical research results; it's an effective complement to Turk.”
"MOOR ...
is an effective complement to [Mechanical] Turk."
-Shriram Krishnamurthi
MOOR will reportedly leverage the contributions of novice scholars from around the globe in an integrated platform that aggregates experimental results and proposed hypotheses. This is combined with a unique algorithm that detects and flags particularly insightful contributions. This will allow research results never before possible, says Joe Gibbs Politz: “I figure only one in 10,000 people can figure out decidable and complete principal type inference for a language with prototype-based inheritance and equirecursive subtyping. So how could we even hope to solve this problem without 10,000 people working on it?”
Krishnamurthi has historically recruited undergraduate Brown students to aid him in his research efforts. Leo Meyerovich, a former Krishnamurthi acolyte, is excited about changing the structure of the educational system, and shares concerns about Krishnamurthi's research program. With the number of undergraduates sure to dwindle to nothing in the coming years, he says, “Shriram will need to come up with some new tricks.”
Brown graduates Ed Lazowska and Peter Norvig appear to agree. While Lazowska refused to comment on behalf of the CRA, saying its position on the matter is “still evolving,” speaking personally, he added, “evolve or die.” As of this writing, Peter Norvig has pledged a set of server farms and the 20% time of 160,000 Google Engineers to support MOOR.
With additional reporting from Kathi Fisler, Hannah Quay-de la Vallee, Benjamin S. Lerner, and Justin Pombrio.
Essentials of Garbage Collection
Tag: Education
Posted on 19 February 2013.How do we teach students the essential ideas behind garbage collection?
A garbage collector (GC) implementation must address many overlapping concerns. There are algorithmic decisions, e.g., the GC algorithm to use; there are representation choices, e.g, the layout of the stack; and there are assumptions about the language, e.g., unforgeable pointers. These choices, and more, affect each other and make it very difficult for students to get off the ground.
Programming language implementations can be similarly complex. However, over the years, starting from McCarthy's seminal paper, we've found it invaluable to write definitional interpreters for simple core languages, that allow us to easily explore the consequences of language design. What is the equivalent for garbage collectors?
Testing and Curricular Dependencies
Testing is important for any program, and is doubly so for a garbage collector, which must correctly deal with complex inputs (i.e., programs!). Furthermore, correctness itself is subtle: besides being efficient, a collector must terminate, be sound (not collect non-garbage), be effective (actually collect enough true garbage), and preserve the essential structure of live data: e.g., given a cyclic datum, it must terminate, and given data with sharing, it must preserve the sharing-structure and not duplicate data.
For instructors, a further concern is the number of deep, curricular dependencies that teaching GC normally incurs. In a course where students already learn compilers and interpreters, it is possible (but hard) to teach GC. However, GC should be teachable in several contexts, such as a systems course, an architecture course, or even as a cool application of graph algorithms. Eliminating GC's curricular dependencies is thus valuable.
Even in courses that have student implement compilers or interpreters, testing a garbage collector is very hard. A test-case is a program that exercises the collector in an interesting way. Good tests require complex programs, and complex programs require a rich programming language. In courses, students tend to write compilers and interpreters for simple, core languages and are thus stuck writing correspondingly simple programs. Worse, some important GC features, such as the treatment of cycles and first-class functions, are impossible to test unless the programming language being implemented has the necessary features. Growing a core language for the sake of testing GC would be a case of the tail wagging the dog.
In short, we would like a pedagogic framework where:
- Students can test their collectors using a full-blown programming language, instead of a stilted core language, and
- Students can experiment with different GC algorithms and data-representations, without learning to implement languages.
The Key Idea
Over the past few years, we've built a framework for teaching garbage collection, first started by former Brown PhD student Greg Cooper.
Consider the following Racket program, which would make a great test-case for a garbage collector (with a suitably small heap):
#lang racket
(define (map f l)
(cond
[(empty? l) empty]
[(cons? l) (cons (f (first l))
(map f (rest l)))]))
(map (lambda (x) (+ x 1)) (list 1 2 3))
As written, Racket's native garbage collector allocates the closure
created by lambda and the lists created by cons
and list. But, what if we could route these calls to a
student-written collector and have it manage memory instead?
Greg made the following simple observation. Why are these values being managed by the Racket memory system? That's because the bindings for lambda, cons and list (and other procedures and values) are provided by #lang racket. Instead, suppose that with just one change, we could swap in a student-written collector:
#lang plai/mutator (allocator-setup "my-mark-and-sweep.rkt" 30)Using the magic of Racket's modules and macros, #lang plai/mutator maps memory-allocating procedures to student-written functions. The student designates a module, such as my-mark-and-sweep that exports a small, prescribed interface for memory allocation. That module allocates values in a private heap and runs its own GC algorithm when it runs out of space. In our framework, the heap size is a parameter that is trivial to change. The program above selects a heap size of 30, which is small enough to trigger several GC cycles.
We've designed the framework so that students can easily swap in different collectors, change the size of the heap, and even use Racket's native collector, as a sanity check.
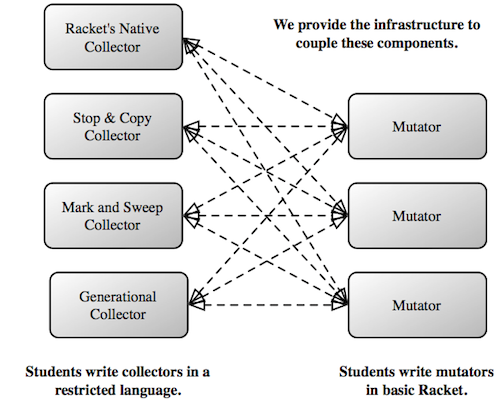
Discovering GC Roots
Routing primitive procedures and constants is only half the story. A collector also needs to inspect and modify the program stack, which holds the roots of garbage collection. Since we allow students to write programs in Racket, the stack is just the Racket stack, which is not open for reflection. Therefore, we must also transform the program to expose the contents of the stack.
Our framework automatically transforms Racket programs to A-normal form, which names all intermediate expressions in each activation record. Unlike other transformations, say CPS, A-normalization preserves stack-layout. This makes it easy for students to co-debug their programs and collectors using the built-in DrRacket debugger.
In addition to inspecting individual activation records, a collector also needs to traverse the entire list of records on the stack. We maintain this list on the stack itself using Racket's continuation marks. Notably, continuation marks preserve tail-calls, so the semantics of Racket programs are unchanged.
The combination of A-normalization and continuation marks gives us a key technical advantage. In their absence, we would have to manually convert programs to continuation-passing style (followed by defunctionalization) to obtain roots. Not only would these be onerous curricular dependencies, but they would make debugging very hard.
Controlling and Visualizing the Heap
Of course, we would like to prevent collectors from cheating. An easy way to cheat is to simply allocate on the Racket heap. We do not go to great lengths to prevent all forms of cheating (these are carefully-graded homeworks, after all). However, we do demand that collectors access the “heap” through a low-level interface (where the heap is actually just one large Racket array). This interface prevents the storage of non-flat values, thereby forcing students to construct compound representations for compound data. Notably, our framework is flexible enough that we have students design their own memory representations.
The low-level heap interface has an added benefit. Because our
framework can tell “where the heap is”, and has access to the
student's heap-inspection procedures, we are able to provide a
fairly effective heap visualizer:

Learn More
We've been using this framework to teach garbage collection for several years at several universities. It is now included with Racket, too. If you'd like to play with the framework, check out one of our GC homework assignments.
A pedagogic paper about this work will appear at SIGCSE 2013.
References
[1] John Clements and Matthias Felleisen. A Tail-Recursive Machine with Stack Inspection. ACM Transactions on Programming Languages and Systems (TOPLAS), Vol. 26, No. 6, November 2004. (PDF)
[2] Gregory H. Cooper, Arjun Guha, Shriram Krishnamurthi, Jay McCarthy, and Robert Bruce Findler. Teaching Garbage Collection without Implementing Compilers or Interpreters. In ACM Technical Symnposium on Computer Science Education (SIGCSE) 2013. (paper)
[3] Cormac Flanagan, Amr Sabry, Bruce F. Duba, and Matthias Felleisen. The Essence of Compiling with Continuations. In ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), 1993. (PDF)
[4] John McCarthy. Recursive Functions of Symbolic Expressions and their Computation by Machine, Part 1. Communications of the ACM, Volume 3, Issue 4, April 1960. (paper)


