Articles by tag: Misconceptions
Misconceptions In Finite-Trace and Infinite-Trace Linear Temporal Logic
Finding and Fixing Standard Misconceptions About Program Behavior
The Examplar Project: A Summary
Conceptual Mutation Testing
Little Tricky Logics
Identifying Problem Misconceptions
Performance Preconceptions
Towards a Notional Machine for Runtime Stacks and Scope
Student Help-Seeking for (Un)Specified Behaviors
Combating Misconceptions by Encouraging Example-Writing
LTL Tutor
Tags: Linear Temporal Logic, Education, Formal Methods, Misconceptions, Properties, Tools, Verification
Posted on 08 August 2024.We have been engaged in a multi-year project to improve education in Linear Temporal Logic (LTL) [Blog Post 1, Blog Post 2]. In particular, we have arrived at a detailed understanding of typical misconceptions that learners and even experts have. Our useful outcome from our studies is a set of instruments (think “quizzes”) that instructors can deploy in their classes to understand how well their students understand the logic and what weaknesses they have.
However, as educators, we recognize that it isn’t always easy to add new materials to classes. Furthermore, your students make certain mistakes—now what? They need explanations of what went wrong, need additional drill problems, and need checks whether they got the additional ones right. It’s hard for an educator to make time for all that. And if one is an independent learner, they don’t even have access to such educators.
Recognizing these practical difficulties, we have distilled our group’s expertise in LTL into a free online tutor:
We have leveraged insights from our studies to create a tool designed to be used by learners with minimal prior instruction. All you need is a brief introduction to LTL (or even just propositional logic) to get started. As an instructor, you can deliver your usual lecture on the topic (using your preferred framing), and then have your students use the tool to grow and to reinforce their learning.
In contrast to traditional tutoring systems, which are often tied to a specific curriculum or course, our tutor adaptively generates multiple-choice question-sets in the context of common LTL misconceptions.
- The tutor provides students who get a question wrong with feedback in terms of their answer’s relationship to the correct answer. Feedback can take the form of visual metaphors, counterexamples, or an interactive trace-stepper that shows the evaluation of an LTL formula across time.

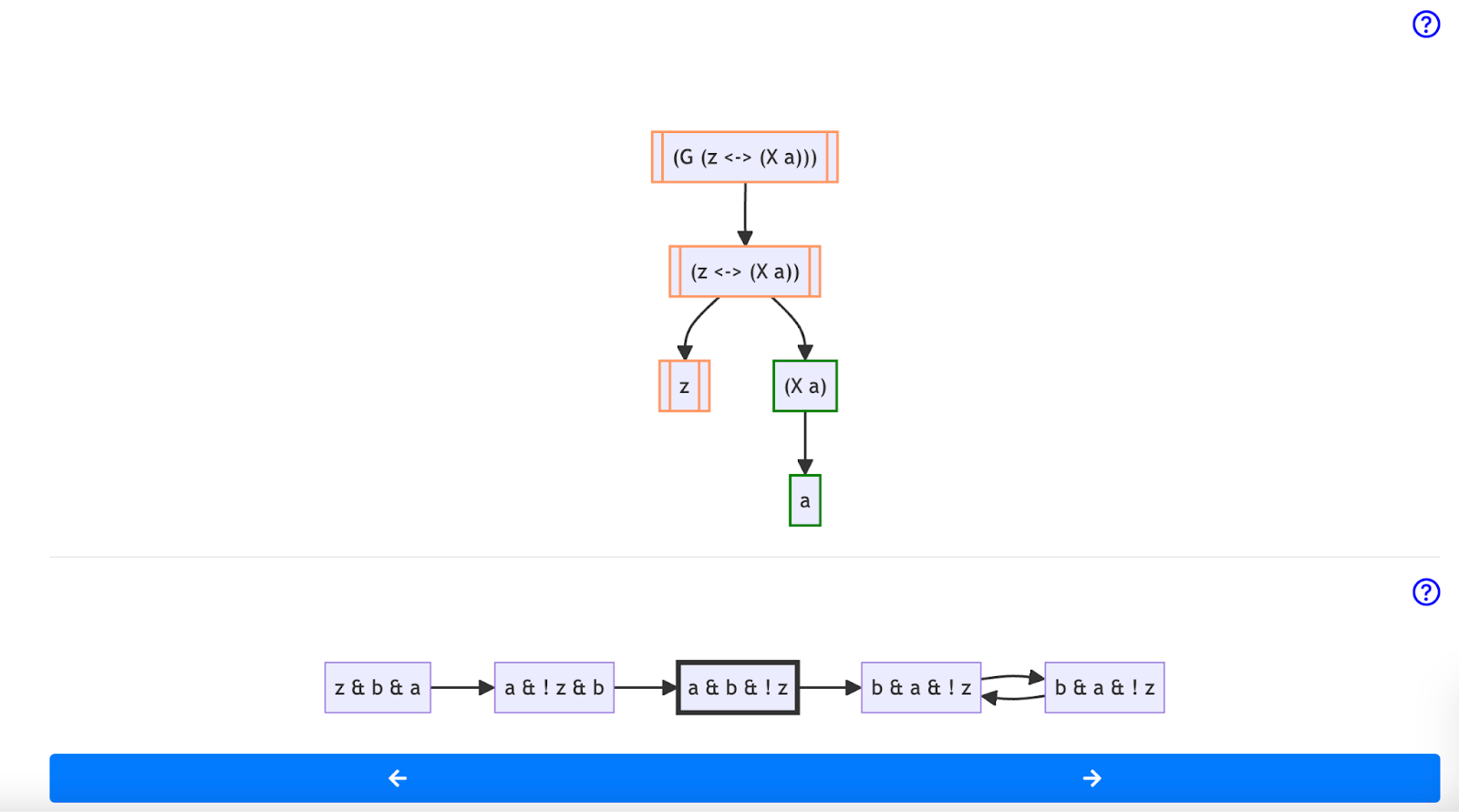
(G (z <-> X(a))) in the third state of a trace. While the overall formula is not satisfied at this moment in time, the sub-formula (X a) is satisfied. This allows learners to explore where their understanding of a formula may have diverged from the correct answer.
- If learners consistently demonstrate the same misconception, the tutor provides them further insight in the form of tailored text grounded in our previous research.
- Once it has a history of misconceptions exhibited by the student, the tutor generates novel, personalized question sets designed to drill students on their specific weaknesses. As students use the tutor, the system updates its understanding of their evolving needs, generating question sets to address newly uncovered or pertinent areas of difficulty.
We also designed the LTL Tutor with practical instructor needs in mind:
- Curriculum Agnostic: The LTL Tutor is flexible and not tied to any specific curriculum. You can seamlessly integrate it into your existing course without making significant changes. It both generates exercises for students and allows you to import your own problem sets.
- Detailed Reporting: To track your class’s progress effectively, you can create a unique course code for your students to enter, so you can get detailed insights into their performance.
- Self-Hostable: If you prefer to have full control over your data, the LTL Tutor can easily be self-hosted.
To learn more about the Tutor, please read our paper!
Misconceptions In Finite-Trace and Infinite-Trace Linear Temporal Logic
Tags: Linear Temporal Logic, Crowdsourcing, Misconceptions, User Studies, Verification
Posted on 07 July 2024.We now also have an automated tutor that puts this material to work to help students directly.
Over the past three years and with a multi-national group of collaborators, we have been digging deeper into misconceptions in LTL (Linear Temporal Logic) and studying misconceptions in LTLf, a promising variant of LTL restricted to finite traces. Why LTL and LTLf? Because beyond their traditional uses in verification and now robot synthesis, they support even more applications, from image processing to web-page testing to process-rule mining. Why study misconceptions? Because ultimately, human users need to fully understand what a formula says before they can safely apply synthesis tools and the like.
Our original post on LTL misconceptions gives more background and motivation. It also explains the main types of questions we use: translations between English specifications and formal specifications.
So what’s new this time around?
First, we provide two test instruments that have been field tested with several audiences:
-
One instrument [PDF] focuses on the delta between LTL and LTLf. If you know LTL but not LTLf, give it a try! You’ll come away with hands-on experience of the special constraints that finite traces bring.
-
The other instrument [PDF] is for LTL beginners — to see what preconceptions they bring to the table. It assumes basic awareness of G (“always”), F (“eventually”), and X (“next state”). It does not test the U (“until”) operator. Live survey here.
Second, we find evidence for several concrete misconceptions in the data. Some misconceptions were identified in prior work and are confirmed here. Others are new to this work.
For example, consider the LTLf formula:
G(red => X(X(red))). What finite traces satisfy it?In particular, can any finite traces that have
redtrue at some point satisfy the formula?Click to show answer:
No, because wheneverredis true it must be true again two states later, but every finite trace will eventually run out of states.
Now consider the LTL formula
F(X(X(red))). Is it true for an infinite trace whereredis true exactly once?Click to show answer:
Yes. But interestingly, some of our LTL beginners said no on the grounds thatX(X(red))ought to "spread out" and constrain three states in a row.
Third, we provide a code book of misconceptions and how to identify them in new data [PDF].
For more details, see the paper.
See also our LTL Tutor (traditional LTL only, not finite-trace).
Finding and Fixing Standard Misconceptions About Program Behavior
Tags: Education, Misconceptions, Semantics, Tools, User Studies
Posted on 12 April 2024.A large number of modern languages — from Java and C# to Python and JavaScript to Racket and OCaml — share a common semantic core:
- variables are lexically scoped
- scope can be nested
- evaluation is eager
- evaluation is sequential (per “thread”)
- variables are mutable, but first-order
- structures (e.g., vectors/arrays and objects) are mutable, and first-class
- functions can be higher-order, and close over lexical bindings
- memory is managed automatically (e.g., garbage collection)
We call this the Standard Model of Languages (SMoL).
SMoL potentially has huge pedagogic benefit:
-
If students master SMoL, they have a good handle on the core of several of these languages.
-
Students may find it easier to port their knowledge between languages: instead of being lost in a sea of different syntax, they can find familiar signposts in the common semantic features. This may also make it easier to learn new languages.
-
The differences between the languages are thrown into sharper contrast.
-
Students can see that, by going beyond syntax, there are several big semantic ideas that underlie all these languages, many of which we consider “best practices” in programming language design.
We have therefore spent the past four years working on the pedagogy of SMoL:
-
Finding errors in the understanding of SMoL program behavior.
-
Finding the (mis)conceptions behind these errors.
-
Collating these into clean instruments that are easy to deploy.
-
Building a tutor to help students correct these misconceptions.
-
Validating all of the above.
We are now ready to present a checkpoint of this effort. We have distilled the essence of this work into a tool:
It identifies and tries to fix student misconceptions. The Tutor assumes users have a baseline of programming knowledge typically found after 1–2 courses: variables, assignments, structured values (like vectors/arrays), functions, and higher-order functions (lambdas). Unlike most tutors, instead of teaching these concepts, it investigates how well the user actually understands them. Wherever the user makes a mistake, the tutor uses an educational device called a refutation text to help them understand where they went wrong and to correct their conception. The Tutor lets the user switch between multiple syntaxes, both so they can work with whichever they find most comfortable (so that syntactic unfamiliarity or discomfort does not itself become a source of errors), and so they can see the semantic unity beneath these languages.
Along the way, to better classify student responses, we invent a concept called the misinterpreter. A misinterpreter is an intentionally incorrect interpreter. Concretely, for each misconception, we create a corresponding misinterpreter: one that has the same semantics as SMoL except on that one feature, where it implements the misconception instead of the correct concept. By making misconceptions executable, we can mechanically check whether student responses correspond to a misconception.
There are many interesting lessons here:
-
Many of the problematic programs are likely to be startlingly simple to experts.
-
The combination of state, aliasing, and functions is complicated for students. (Yet most introductory courses plunge students into this maelstrom of topics without a second thought or care.)
-
Misinterpreters are an interesting concept in their own right, and are likely to have value independent of the above use.
In addition, we have not directly studied the following claims but believe they are well warranted based on observations from this work and from experience teaching and discussing programming languages:
-
In SMoL languages, local and top-level bindings behave the same as the binding induced by a function call. However, students often do not realize that these have a uniform semantics. In part this may be caused by our focus on the “call by” terminology, which focuses on calls (and makes them seem special). We believe it would be an improvement to replace these with “bind by”.
-
We also believe that the terms “call-by-value” and “call-by-reference” are so hopelessly muddled at this point (between students, instructors, blogs, the Web…) that finding better terminology overall would be helpful.
-
The way we informally talk about programming concepts (like “pass a variable”), and the syntactic choices our languages make (like
return x), are almost certainly also sources of confusion. The former can naturally lead students to believe variables are being aliased, and the latter can lead them to believe the variable, rather than its value, is being returned.
For more details about the work, see the paper. The paper is based on an old version of the Tutor, where all programs were presented in parenthetical syntax. The Tutor now supports multiple syntaxes, so you don’t have to worry about being constrained by that. Indeed, it’s being used right now in a course that uses Scala 3.
Most of all, the SMoL Tutor is free to use! We welcome and encourage instructors of programming courses to consider using it — you may be surprised by the mistakes your students make on these seemingly very simple programs. But we also welcome learners of all stripes to give it a try!
The Examplar Project: A Summary
Tags: Education, Misconceptions, Testing, Tools
Posted on 01 January 2024.For the past several years, we have worked on a project called Examplar. This article summarizes the goals and methods of the project and provides pointers to more detailed articles describing it.
Context
When faced with an programming problem, computer science students all-too-often begin their implementations with an incomplete understanding of what the problem is asking, and may not realize until far into their development process (if at all) that they have solved the wrong problem. At best, a student realizes their mistake, suffers from some frustration, and is able to correct it before the final submission deadline. At worst, they might not realize their mistake until they receive feedback on their final submission, depriving them of the intended learning goal of the assignment.
How can we help them with this? A common practice—used across disciplines—is to tell students, “explain the problem in your own words”. This is a fine strategy, except it demands far too much of the student. Any educator who has done this knows that most students rightly stumble through this exercise, usually because they don’t have any better words than are already in the problem statement. So what was meant to be a comprehension exercise becomes a literary one; even if they can restate it very articulately, it may be because of verbal skills, not necessarily indicative of good understanding. And for complex problems, the whole exercise is somewhat futile. It’s all made even more difficult when students are not in their native language, etc.
So we have the kernel of a good idea—asking students to read back their understanding—but words are a poor medium for it.
Examples
Our idea is that writing examples—using the syntax of text cases—is a great way to express understanding:
-
Examples are concrete.
-
It’s hard to be vague.
-
Difficulty writing down examples is usually indicative of broader difficulties with the problem, and a great, concrete way to initiate a discussion with course staff.
-
It gets a head-start on writing tests, which too many computing curricula undervalue (if they tackle it at all).
Best of all, because the examples are executable, they can be run against implementations so that students get immediate feedback.
Types of Feedback
We want to give two kinds of feedback:
-
Correctness: Are they even correct? Do they match the problem specification?
-
Thoroughness: How much of the problem space do they cover? Do they dodge misconceptions?
Consider (for example!) the median function. Here are two examples, in the syntax of Pyret:
check:
median([list: 1, 2, 3]) is 2
median([list: 1, 3, 5]) is 3
end
These are both correct, as running them against a correct implementation of median will confirm, but are they thorough?
A student could, for instance, easily mistake median for mean. Note that the two examples above do not distinguish between the two functions! So giving students a thumbs-up at this point may still send them down the wrong path: they haven’t expressed enough of an understanding of the problem.
Evaluating Examples
For this reason, Examplar runs a program against multiple implementations. One is a correct implementation (which we call the wheat). (For technical reasons, it can be useful to have more than one correct implementation; see more below.) There are also several buggy implementations (called chaffs). Each example is first run against the wheat, to make sure it conforms to the problem specification. It is then run against each of the chaffs. Here’s what a recent version looks like:
Every example is a classifier: its job is to classify a program as correct or incorrect, i.e., to separate the wheat from the chaff. Of course, a particular buggy implementation may not be buggy in a way that a particular example catches. But across the board, the collection of examples should do a fairly good job of catching the buggy examples.
Thus, for instance, one of our buggy implementations of median would be mean. Because the two examples above are consistent with mean as well, they would (incorrectly) pass mean instead of signaling an error. If we had no other examples in our suite, we would fail to catch mean as buggy. That reflects directly as “the student has not yet confirmed that they understand the difference between the two functions”. We would want students to add examples like
median([list: 1, 3, 7]) is 3
that pass median but not mean to demonstrate that they have that understanding.
Answering Questions
Examplar is also useful as a “24 hour TA”. Consider this example:
median([list: 1, 2, 3, 4]) is ???
What is the answer? There are three possible answers: the left-median (2), right-median (3), and mean-median (2.5). A student could post on a forum and wait for a course staffer to read and answer. Or they can simply formulate the question as a test: e.g.,
median([list: 1, 2, 3, 4]) is 2.5
One of these three will pass the wheat. That tells the student the definition being used for this course, which may not have been fully specified in the problem statement. Similarly:
median([list: ]) is ??? # the empty list
Indeed, we see students coming to course staff with questions like, “I see that Examplar said that …, and I wanted to know why this is the answer”, which is a fantastic kind of question to hear.
Whence Chaffs?
It’s easy to see where to get the wheat: it’s just a correct implementation of the problem. But how do we get chaffs?
An astute reader will have noticed that we are practicing a form of mutation testing. Therefore, it might be tempting to use mutation testing libraries to generate chaffs. This would be a mistake because it misunderstands the point of Examplar.
We want students to use Examplar before they start programming, and as a warm-up activity to get their minds into the right problem space. That is not the time to be developing a test suite so extensive that it can capture every strange kind of error that might arise. Rather, we think of Examplar as performing what we call conceptual mutation testing: we only want to make sure they have the right conception of the problem, and avoid misconceptions about it. Therefore, chaffs should correspond to high-level conceptual mistakes (like confusing median and mean), not low-level programming errors.
Whence Misconceptions?
There are many ways to find out what misconceptions students have. One is by studying the errors we ourselves make while formulating or solving the problem. Another is by seeing what kinds of questions they ask course staff and what corrections we need to make. But there’s one more interesting and subtle source: Examplar itself!
Remember how we said we want examples to first pass the wheat? The failing ones are obviously…well, they’re wrong, but they may be wrong for an interesting reason. For instance, suppose we’ve defined median to produce the mean-median. Now, if a student writes
median([list: 1, 2, 3, 4]) is 3
they are essentially expressing their belief that they need to solve the right-median problem. Thus, by harvesting these “errors”, filtering, and then clustering them, we can determine what misconceptions students have because they told us—in their own words!
Readings
-
Why you might want more than one wheat: paper
-
Student use without coercion (in other words, gamified interfaces help…sometimes a bit too much): blog; paper
-
What help do students need that Examplar can’t provide? blog; paper
But this work has much earlier origins:
-
How to Design Programs has students write tests before programs. However, these tests are inert (i.e., there’s nothing to run them against), so students see little value in doing so. Examplar eliminates this inertness, and goes further.
-
Before Examplar, we had students provide peer-review on tests, and found it had several benefits: paper. We also built a (no longer maintained) programming environment to support peer review: paper.
-
One thing we learned is that these test suites can grow too large to generate useful feedback. This caused us to focus on the essential test cases, out of which the idea of examples (as opposed to tests) evolved: paper.
Conceptual Mutation Testing
Tags: Education, Misconceptions, Testing, Tools, User Studies
Posted on 31 October 2023.Here’s a summary of the full arc, including later work, of the Examplar project.
The Examplar system is designed to solve the documented phenomenon that students often misunderstand a programming problem statement and hence “solve” the wrong problem. It does so by asking students to begin by writing input/output examples of program behavior, and evaluating them against correct and buggy implementations of the solution. Students refine and demonstrate their understanding of the problem by writing examples that correctly classify these implementations.

It is, however, very difficult to come up with good buggy candidates. These programs must correspond to the problem misconceptions students are most likely to have. Students can, otherwise, end up spending too much time catching them, and not enough time on the actual programming task. Additionally, a small number of very effective buggy implementations is far more useful than either a large number or ineffective ones (much less both).
Our previous research has shown that student-authored examples that fail the correct implementation often correspond to student misconceptions. Buggy implementations based on these misconceptions circumvent many of the pitfalls of expert-generated equivalents (most notably the ‘expert blind spot’). That work, however, leaves unanswered the crucial question of how to operationalize class-sourced misconceptions. Even a modestly sized class can generate thousands of failing examples per assignment. It takes a huge amount of manual effort, expertise, and time to extract misconceptions from this sea of failing examples.
The key is to cluster these failing examples. The obvious clustering method – syntactic – fails miserably: small syntactic differences can result in large semantic differences, and vice versa (as the paper shows). Instead, we need a clustering technique that is based on the semantics of the problem.
This paper instead presents a conceptual clustering technique based on key characteristics of each programming assignment. These clusters dramatically shrink the space that must be examined by course staff, and naturally suggest techniques for choosing buggy implementation suites. We demonstrate that these curated buggy implementations better reflect student misunderstandings than those generated purely by course staff. Finally, the paper suggests further avenues for operationalizing student misconceptions, including the generation of targeted hints.
You can learn more about the work from the paper.
Little Tricky Logics
Tags: Linear Temporal Logic, Crowdsourcing, Misconceptions, User Studies, Verification
Posted on 05 November 2022.We also have followup work that continues to explore LTL and now also studies finite-trace LTL. In addition, we also have an automated tutor that puts this material to work to help students directly.
LTL (Linear Temporal Logic) has long been central in computer-aided verification and synthesis. Lately, it’s also been making significant inroads into areas like planning for robots. LTL is powerful, beautiful, and concise. What’s not to love?
However, any logic used in these settings must also satisfy the central goal of being understandable by its users. Especially in a field like synthesis, there is no second line of defense: a synthesizer does exactly what the specification says. If the specification is wrong, the output will be wrong in the same way.
Therefore, we need to understand how people comprehend these logics. Unfortunately, the human factors of logics has seen almost no attention in the research community. Indeed, if anything, the literature is rife with claims about what is “easy” or “intuitive” without any rigorous justification for such claims.
With this paper, we hope to change that conversation. We bring to bear on this problem several techniques from diverse areas—but primarily from education and other social sciences (with tooling provided by computer science)—to understand the misconceptions people have with logics. Misconceptions are not merely mistakes; they are validated understanding difficulties (i.e., having the wrong concept), and hence demand much greater attention. We are especially inspired by work in physics education on the creation of concept inventories, which are validated instruments for rapidly identifying misconceptions in a population, and take steps towards the creation of one.
Concretely, we focus on LTL (given its widespread use) and study the problem of LTL understanding from three different perspectives:
-
LTL to English: Given an LTL formula, can a reader accurately translate it into English? This is similar to what a person does when reading a specification, e.g., when code-reviewing work or studying a paper.
-
English to LTL: Given an English statement, can a reader accurately express it in LTL? This skill is essential for specification and verification.
Furthermore, “understanding LTL” needs to be divided into two parts: syntax and semantics. Therefore, we study a third issue:
- Trace satisfaction: Given an LTL formula and a trace (sequence of states), can a reader accurately label the trace as satisfying or violating? Such questions directly test knowledge of LTL semantics.
Our studies were conducted over multiple years, with multiple audiences, and using multiple methods, with both formative and confirmatory phases. The net result is that we find numerous misconceptions in the understanding of LTL in all three categories. Notably, our studies are based on small formulas and traces, so we expect the set of issues will only grow as the instruments contain larger artifacts.
Ultimately, in addition to
- finding concrete misconceptions,
we also:
-
create a codebook of misconceptions that LTL users have, and
-
provide instruments for finding these misconceptions.
We believe all three will be of immediate use to different communities, such as students, educators, tool-builders, and designers of new logic-based languages.
For more details, see the paper.
See also our LTL Tutor.
Identifying Problem Misconceptions
Tags: Education, Misconceptions, Testing, Tools
Posted on 15 October 2022.Here’s a summary of the full arc, including later work, of the Examplar project.
Our recent work is built on the documented research that students often misunderstand a programming problem statement and hence “solve” the wrong problem. This not only creates frustration and wastes time, it also robs them of whatever learning objective motivated the task.
To address this, the Examplar system asks students to first write examples. These examples are evaluated against wheats (correct implementations) and chaffs (buggy implementations). Examples must pass the wheat, and correctly identify as wrong as many chaffs as possible. Prior work explores this and shows that it is quite effective.
However, there’s a problem with chaffs. Students can end up spending too much time catching them, and not enough time on the actual programming task. Therefore, you want chaffs that correspond to the problem misconceptions students are most likely to have. Having a small number of very effective chaffs is far more useful than either a large number or ineffective ones (much less both). But the open question has always been, how do we obtain chaffs?
Previously, chaffs were created by hand by experts. This was problematic because it forces experts to imagine the kinds of problems students might have; this is not only hard, it is bound to run into expert blind spots. What other method do we have?
This work is based on a very simple, clever observation: any time an example fails a wheat, it may correspond to a student misconception. Of course, not all wheat failures are misconceptions! It could be a typo, it could be a basic logical error, or it could even be an attempt to game the wheat-chaff system. Do we know in what ratio these occur, and can we use the ones that are misconceptions?
This paper makes two main contributions:
-
It shows that that many wheat failures really are misconceptions.
-
It uses these misconceptions to formulate new chaffs, and shows that they compare very favorably to expert-generated chaffs.
Furthermore, the work spans two kinds of courses: one is an accelerated introductory programming class, while the other is an upper-level formal methods course. We show that there is value in both settings.
This is just a first step in this direction; a lot of manual work went into this research, which needs to be automated; we also need to measure the direct impact on students. But it’s a very promising direction in a few ways:
-
It presents a novel method for finding misconceptions.
-
It naturally works around expert blind-spots.
-
With more automation, it can be made lightweight.
In particular, if we can make it lightweight, we can apply it to settings—even individual homework problems—that also manifest misconceptions that need fixing, but could never afford heavyweight concept-inventory-like methods for identifying them.
You can learn more about the work from the paper.
Performance Preconceptions
Tags: Education, Misconceptions, User Studies
Posted on 10 October 2022.What do computer science students entering post-secondary (collegiate) education think “performance” means?
Who or what shapes these views?
How accurate are these views?
And how correctable are their mistakes?
These questions are not merely an idle curiosity. How students perceive performance impacts how they think about program design (e.g., they may think a particular design is better but still not use it because they think it’s less performant). It also affects their receptiveness to new programming languages and styles (“paradigms”) of programming. Anecdotally, we have seen exactly these phenomena at play in our courses.
We are especially interested in students who have had prior computer science (in secondary school), such as students taking the AP Computer Science exam in the US. These students often have significant prior computing, but we have studied relatively little about the downstream consequences of these courses. Indeed, performance considerations are manifest in material as early as the age 4–8 curriculum from Code.org!
This paper takes a first step in examining these issues. We find that students have high confidence in incorrect answers on material they should have little confidence about. To address these problems, we try multiple known techniques from the psychology and education literature — the Illusion of Explanatory Depth, and Refutation Texts — that have been found to work in several other domains. We see that they have little impact here.
This work has numerous potential confounds based on the study design and location of performance. Therefore, we don’t view this as a definitive result, but rather as a spur to start an urgently-needed conversation about factors that affect post-secondary computer science education. Concretely, as we discuss in the discussion sections, we also believe there is very little we know about how students conceive of “performance”, and question whether our classical methods for approaching it are effective.
The paper is split into a short paper, that summarizes the results, an an extensive appendix, which provides all the details and justifies the summary. Both are available online.
Towards a Notional Machine for Runtime Stacks and Scope
Tags: Education, Misconceptions, Scope, Semantics, User Studies
Posted on 07 July 2022.Stacks are central to our understanding of program behavior; so is scope. These concepts become ever more important as ever more programming languages embrace concepts like closures and advanced control (like generators). Furthermore, stacks and scope interact in an interesting way, and these features really exercise their intersection.
Over the years we’ve seen students exhibit several problematic conceptions about stacks (and scope). For instance, consider a program like this:
def f(x):
return g(x + 1)
def g(y):
return y + x
f(3)
What is its value? You want an error: that x is not bound. But think
about your canonical stack diagram for this program. You have a frame
for g atop that for x, and you have been told that you “look down
the stack”. (Or vice versa, depending on how your stacks grow.) So
it’s very reasonable to conclude that this program produces 7, the
result produced by dynamic scope.
We see students thinking exactly this.
Consider this program:
def f(x):
return lambda y: x + y
p = f(3)
p(4)
This one, conversely, should produce 7. But students who have been
taught a conventional notion of call-and-return assume that f’s
stack frame has been removed after the call completed (correct!), so
p(4) must result in an error that x is not bound.
We see students thinking exactly this, too.
The paper sets out to do several things.
First, we try to understand the conceptions of stacks that students have coming into an upper-level programming languages course. (It’s not great, y’all.)
Second, we create some tooling to help students learn more about stacks. More on that below. The tooling seems to work well for students who get some practice using it.
Third, we find that even after several rounds of direct instruction and practice, some misconceptions remain. In particular, students do not properly understand how environments chain to get scope right.
Fourth, in a class that had various interventions including interpreters, students did much better than in a class where students learned from interpreters alone. Though we love interpreters and think they have various valuable uses in programming languages education, our results make us question some of the community’s beliefs about the benefits of using interpreters. In particular, some notions of transfer that we would have liked to see do not occur. We therefore believe that the use of interpreters needs much more investigation.
As for the tooling: One of the things we learned from our initial study is that students simply do not have a standardized way of presenting stacks. What goes in them, and how, were all over the map. We conjecture there are many reasons: students mostly see stacks and are rarely asked to draw them; and when they do, they have no standard tools for doing so. So they invent various ad hoc notations, which in turn don’t necessarily reinforce all the aspects that a stack should represent.
We therefore created a small tool for drawing stacks. What we did was repurpose Snap! to create a palette of stack, environment, and heap blocks. It’s important to understand these aren’t runnable programs: these are just static representations of program states. But Snap! is fine with that. This gave us a consistent notation that we could use everywhere: in class, in the textbook, and in homeworks. The ability to make stacks very quickly with drag-and-drop was clearly convenient to students who gained experience with the tool, because many used it voluntarily; it was also a huge benefit for in-class instruction over a more conventional drawing tool. An unexpected success for block syntaxes!
For more details, see the paper.
Student Help-Seeking for (Un)Specified Behaviors
Tags: Education, Misconceptions, Testing, Tools, User Studies
Posted on 02 October 2021.Here’s a summary of the full arc, including later work, of the Examplar project.
Over the years we have done a lot of work on Examplar, our system for helping students understand the problem before they start implementing it. Given that students will even use it voluntarily (perhaps even too much), it would seem to be a success story.
However, a full and fair scientific account of Examplar should also examine where it fails. To that end, we conducted an extensive investigation of all the posts students made on our course help forum for a whole semester, identified which posts had to do with problem specification (and under-specification!), and categorized how helpful or unhelpful Examplar was.
The good news is we saw several cases where Examplar had been directly helpful to students. These should indeed be considered a lower-bound, because the point of Examplar is to “answer” many questions directly, so they would never even make it onto the help forum.
But there is also bad news. To wit:
-
Students sometimes simply fail to use Examplar’s feedback; is this a shortcoming of the UI, of the training, or something inherent to how students interact with such systems?
-
Students tend to overly focus on inputs, which are only a part of the suite of examples.
-
Students do not transfer lessons from earlier assignments to later ones.
-
Students have various preconceptions about problem statements, such as imagining functionality not asked for or constraints not imposed.
-
Students enlarge the specification beyond what was written.
-
Students sometimes just don’t understand Examplar.
These serve to spur future research in this field, and may also point to the limits of automated assistance.
To learn more about this work, and in particular to get the points above fleshed out, see our paper!
Combating Misconceptions by Encouraging Example-Writing
Tags: Education, Misconceptions, Testing, Tools
Posted on 11 January 2020.Here’s a summary of the full arc, including later work, of the Examplar project.
When faced with an unfamiliar programming problem, undergraduate computer science students all-too-often begin their implementations with an incomplete understanding of what the problem is asking, and may not realize until far into their development process (if at all) that they have solved the wrong problem. At best, a student realizes their mistake, suffers from some frustration, and is able to correct it before the final submission deadline. At worst, they might not realize their mistake until they receive feedback on their final submission—depriving them of the intended learning goal of the assignment.
Educators must therefore provide students with some mechanism by which students can evaluate their own understanding of a problem—before they waste time implementing some misconceived variation of that problem. To this end, we provide students with Examplar: an IDE for writing input–output examples that provides on-demand feedback on whether the examples are:
- valid (consistent with the problem), and
- thorough (explore the conceptually interesting corners of the problem).
For a demonstration, watch this brief video!
With its gamification, we believed students would find Examplar compelling to use. Moreover, we believed its feedback would be helpful. Both of these hypotheses were confirmed. We found that students used Examplar extensively—even when they were not required to use it, and even for assignments for which they were not required to submit test cases. The quality of students’ final submissions generally improved over previous years, too. For more information, read the full paper here!

