Articles by tag: Resugaring

Resugaring Type Rules
A Third Perspective on Hygiene
Scope Inference, a.k.a. Resugaring Scope Rules
Resugaring Evaluation Sequences
Slimming Languages by Reducing Sugar

Resugaring Type Rules

Tags: Programming Languages, Resugaring, Semantics, Types

Posted on 19 June 2018.

This is the final post in a series about resugaring. It focuses on resugaring type rules. See also our posts on resugaring evaluation steps and resugaring scope rules.

No one should have to see the insides of your macros. Yet type errors often reveal them. For example, here is a very simple and macro in Rust (of course you should just use && instead, but we’ll use this as a simple working example):

and the type error message you get if you misuse it:

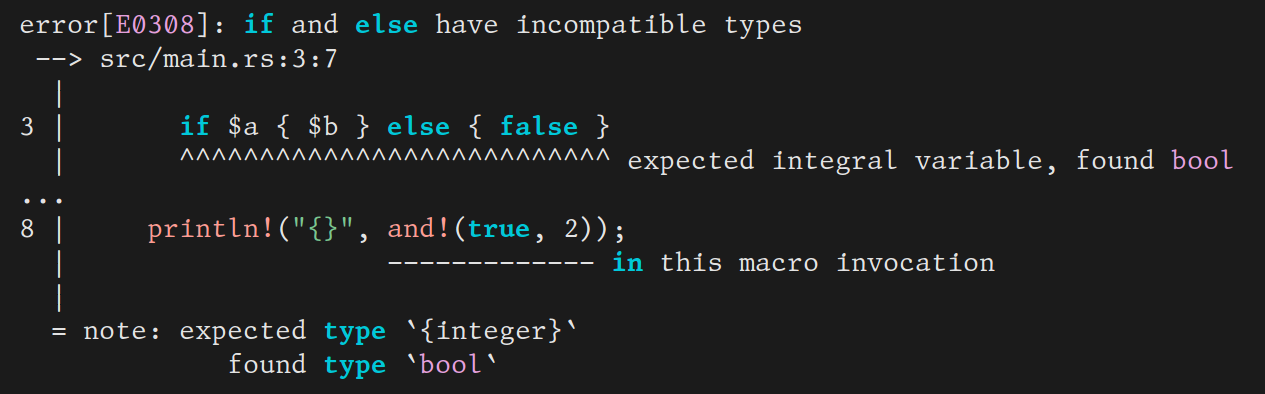
You can see that it shows you the definition of this macro. In this case it’s not so bad, but other macros can get messy, and you might not want to see their guts. Plus in principle, a type error should only show the erronous code, not correct code that it happend to call. You wouldn’t be very happy with a type checker that sometimes threw an error deep in the body of a (type correct) library function that you called, just because you used it the wrong way. Why put up with one that does the same thing for macros?

The reason Rust does is that that it does not know the type of and. As a result, it can only type check after and has been desugared (a.k.a., expanded), and so the error occurs in the desugared code.

But what if Rust could automatically infer a type rule for checking and, using only the its definition? Then the error could be found in the original program that you wrote (rather than its expansion), and presented as such. This is exactly what we did—albeit for simpler type systems than Rust’s—in our recent PLDI’18 paper Inferring Type Rules for Syntactic Sugar.

We call this process resugaring type rules; akin to our previous work on resugaring evaluation steps and resugaring scope rules. Let’s walk through the resugaring of a type rule for and:

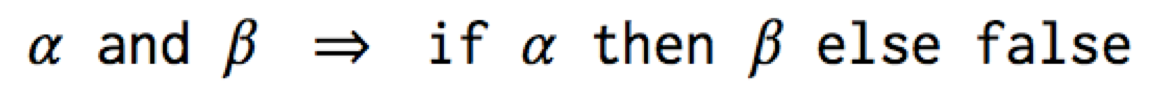
We want to automatically derive a type rule for and, and we want it to be correct. But what does it mean for it to be correct? Well, the meaning of and is defined by its desugaring: α and β is synonymous with if α then β else false. Thus they should have the same type:

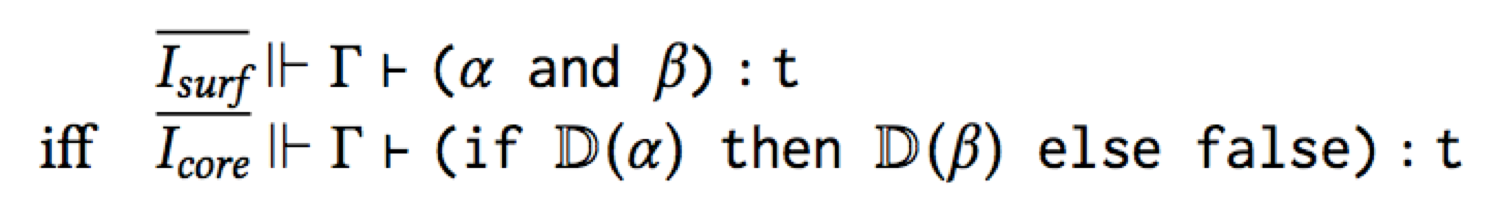
(Isurf ||- means “in the surface language type system”, Icore ||- means “in the core language type system”, and the fancy D means “desugar”.)

How can we achieve this? The most straightforward to do is to capture the iff with two type rules, one for the forward implication, and one for the reverse:

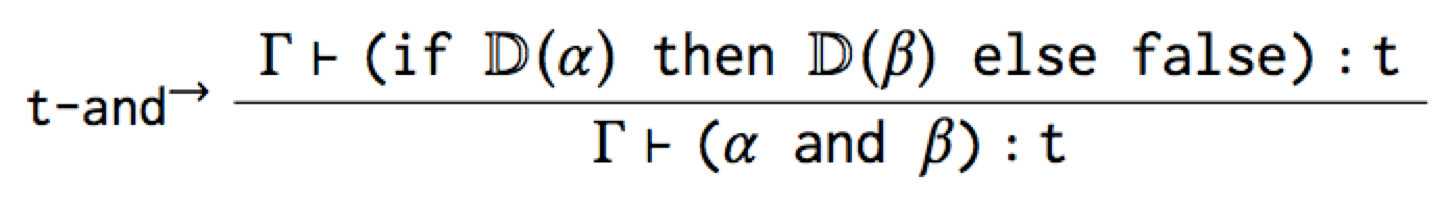
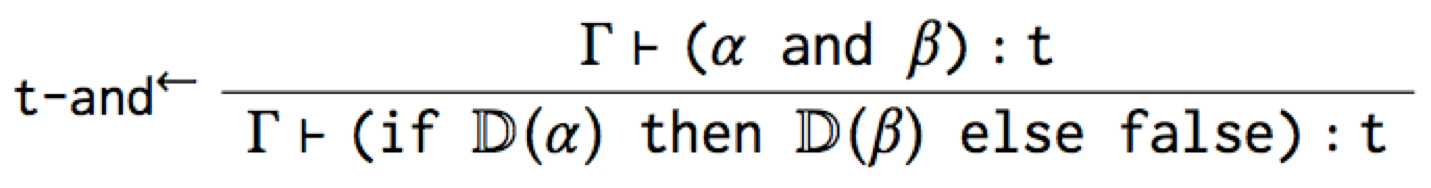
The first type rule is useful because it says how to type check and in terms of its desugaring. For example, here’s a derivation that true and false has type Bool:

However, while this t-and^→ rule is accurate, it’s not the canonical type rule for and that you’d expect. And worse, it mentions if, so it’s leaking the implementation of the macro!

However, we can automatically construct a better type rule. The trick is to look at a more general derivation. Here’s a generic type derivation for any term α and β:

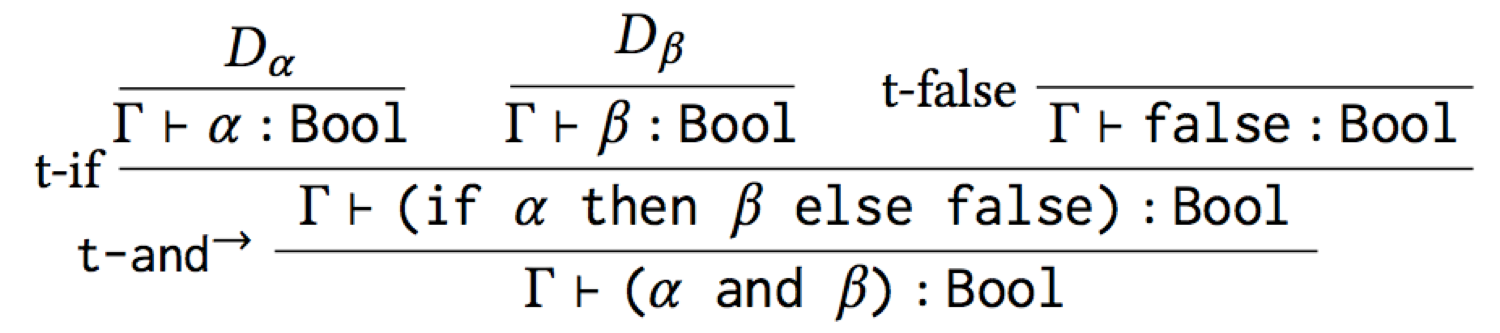
Notice D_α and D_β: these are holes in the derivation, which ought to be filled in with sub-derivations proving that α has type Bool and β has type Bool. Thus, “α : Bool” and “β : Bool” are assumptions we must make for the type derivation to work. However, if these assumptions hold, then the conclusion of the derivation must hold. We can capture this fact in a type rule, whole premises are these assumptions, and whose conclusion is the conclusion of the whole derivation:

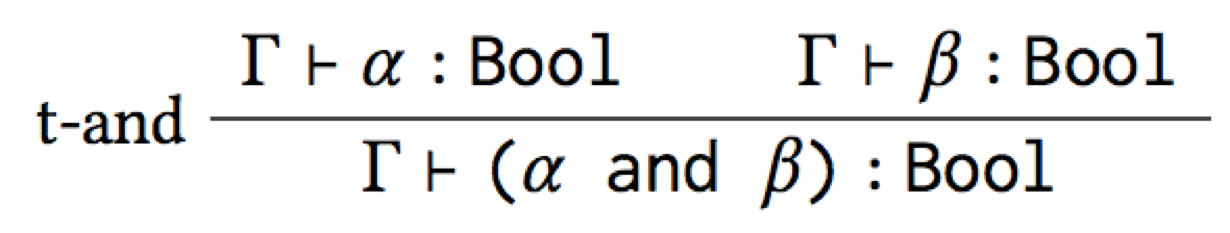
And so we’ve inferred the canonical type rule for and! Notice that (i) it doesn’t mention if at all, so it’s not leaking the inside of the macro, and (ii) it’s guaranteed to be correct, so it’s a good starting point for fixing up a type system to present errors at the right level of abstraction. This was a simple example for illustrative purposes, but we’ve tested the approach on a variety of sugars and type systems.

You can read more in our paper, or play with the implementation.

A Third Perspective on Hygiene

Tags: Programming Languages, Resugaring, Scope, Semantics

Posted on 20 June 2017.

In the last post, we talked about scope inference: automatically inferring scoping rules for syntatic sugar. In this post we’ll talk about the perhaps surprising connection between scope inference and hygiene.

Hygiene can be viewed from a number of perspectives and defined in a number of ways. We’ll talk about two pre-existing perspectives, and then give a third perspective that comes from having scope inference.

First Perspective

The traditional perspective on hygiene (going all the way back to Kohlbecker in ’86) defines it by what shouldn’t happen when you expand macros / syntactic sugar. To paraphrase the idea:

Expanding syntactic sugar should not cause accidental variable capture. For instance, a variable used in a sugar should not come to refer to a variable declared in the program simply because it has the same name.

Thus, hygiene in this tradition is defined by a negative.

It has also traditionally focused strongly on algorithms. One would expect papers on hygiene to state a definition of hygiene, give an algorithm for macro expansion, and then prove that the algorithm obeys these properties. But this last step, the proof, is usually suspiciously missing. At least part of the reason for this, we suspect, is that definitions of hygiene have been too informal to be used in a proof.

And a definition of hygiene has been surprisingly hard to pin down precisely. In 2015, a full 29 years after Kohlbecker’s seminal work, Adams writes that “Hygiene is an essential aspect of Scheme’s macro system that prevents unintended variable capture. However, previous work on hygiene has focused on algorithmic implementation rather than precise, mathematical definition of what constitutes hygiene.” He goes on to discuss “observed-binder hygiene”, which is “not often discussed but is implicitly averted by traditional hygiene algorithms”. The point we’re trying to make is that the traditional view on hygiene is subtle.

Second Perspective

There is a much cleaner definition of hygiene, however, that is more of a positive statement (and subsumes the preceding issues):

If two programs are α-equivalent (that is, they are the same up to renaming variables), then when you desugar them (that is, expand their sugars) they should still be α-equivalent.

Unfortunately, this definition only makes sense if we have scope defined on both the full and base languages. Most hygiene systems can’t use this definition, however, because the full language is not usually given explicit scoping rules; rather, it’s defined implicitly through translation into the base language.

Recently, Herman and Wand have advocated for specifying the scoping rules for the full language (in addition to the base language), and then verifying that this property holds. If the property doesn’t hold, then either the scope specification or the sugar definitions are incorrect. This is, however, an onerous demand to place on the developer of syntactic sugar, especially since scope can be surprisingly tricky to define precisely.

Third Perspective

Scope inference gives a third perspective. Instead of requiring authors of syntactic sugar to specify the scoping rules for the full language, we give an algorithm that infers them. We have to then define what it means for this algorithm to work “correctly”.

We say that an inferred scope is correct precisely if the second definition of hygiene holds: that is, if desugaring preserves α-equivalence. Thus, our scope inference algorithm finds scoping rules such that this property holds, and if no such scoping rules exist then it fails. (And if there are multiple sets of scoping rules to choose from, it chooses the ones that put as few names in scope as possible.)

An analogy would be useful here. Think about type inference: it finds type annotations that could be put in your program such that it would type check, and if there are multiple options then it picks the most general one. Scope inference similarly finds scoping rules for the full language such that desugaring preserves α-equivalence, and if there are multiple options then it picks the one that puts the fewest names in scope.

This new perspective on hygiene allows us to shift the focus from expansion algorithms to the sugars themselves. When your focus is on an expansion algorithm, you have to deal with whatever syntactic sugar is thrown your way. If a sugar introduces unbound identifiers, then the programmer (who uses the macro) just has to deal with it. Likewise, if a sugar uses scope inconsistently, treating a variable either as a declaration or a reference depending on the phase of the moon, the programmer just has to deal with it. In contrast, since we infer scope for the full language, we check check weather a sugar would do one of these bad things, and if so we can call the sugar unhygienic.

To be more concrete, consider a desugaring rule for bad(x, expression) that sometimes expands to lambda x: expression and sometimes expands to just expression, depending on the context. Our algorithm would infer from the first rewrite that the expression must be in scope of x. However, this would mean that the expression was allowed to contain references to x, which would become unbound when the second rewrite was used! Our algorithm detects this and rejects this desugaring rule. Traditional macro systems allow this, and only detect the potential unbound identifier problem when it actually occurred. The paper contains a more interesting example called “lambda flip flop” that is rejected because it uses scope inconsistently.

Altogether, scope inference rules out bad sugars that cannot be made hygienic, but if there is any way to make a sugar hygienic it will find it.

Again, here’s the paper and implementation, if you want to read more or try it out.

Scope Inference, a.k.a. Resugaring Scope Rules

Tags: Programming Languages, Pyret, Resugaring, Scope, Semantics

Posted on 12 June 2017.

This is the second post in a series about resugaring. It focuses on resugaring scope rules. See also our posts on resugaring evaluation steps and resugaring type rules.

Many programming languages have syntactic sugar. We would hazard to guess that most modern languages do. This is when a piece of syntax in a language is defined in terms of the rest of the language. As a simple example, x += expression might be shorthand for x = x + expression. A more interesting sugar is Pyret’s for loops. For example:

for fold(p from 1, n from range(1, 6)):
  p * n
end

computes 5 factorial, which is 120. This for is a piece of sugar, though, and the above code is secretly shorthand for:

fold(lam(p, n): p * n end, 1, range(1, 6))

Sugars like this are great for language development: they let you grow a language without making it more complicated.

Languages also have scoping rules that say where variables are in scope. For instance, the scoping rules should say that a function’s parameters are in scope in the body of the function, but not in scope outside of the function. Many nice features in editors depend on these scoping rules. For instance, if you use autocomplete for variable names, it should only suggest variables that are in scope. Similarly, refactoring tools that rename variables need to know what is in scope.

This breaks down in the presence of syntactic sugar, though: how can your editor tell what the scoping rules for a sugar are?

The usual approach is to write down all of the scoping rules for all of the sugars. But this is error prone (you need to make sure that what you write down matches the actual behavior of the sugars), and tedious. It also goes against a general principle we hold: to add a sugar to a language, you should just add the sugar to the language. You shouldn’t also need to update your scoping rules, or update your type system, or update your debugger: that should all be done automatically.

We’ve just published a paper at ICFP that shows how to automatically infer the scoping rules for a piece of sugar, like the for example above. Here is the paper and implementation. This is the latest work we’ve done with the goal of making the above principle a reality. Earlier, we showed how to automatically find evaluation steps that show how your program runs in the presence of syntatic sugar.

How it Works

Our algorithm needs two things to run:

The definitions of syntactic sugar. These are given as pattern-based rewrite rules, saying what patterns match and what they should be rewritten to.
The scoping rules for the base (i.e. core) language.

It then automatically infers scoping rules for the full language, that includes the sugars. The final step to make this useful would be to add these inferred scoping rules to editors that can use them, such as Sublime, Atom, CodeMirror, etc.

For example, we have tested it on Pyret (as well as other languages). We gave it scoping rules for Pyret’s base language (which included things like lambdas and function application), and we gave it rules for how for desugars, and it determined the scoping rules of for. In particular:

The variables declared in each from clause are visible in the body, but not in the argument of any from clause.
If two from clauses both declare the same variable, the second one shadows the first one.

This second rule is exactly the sort of thing that is easy to overlook if you try to write these rules down by hand, resulting in obscure bugs (e.g. when doing automatic variable refactoring).

Here are the paper and implementation, if you want to read more or try it out.

Resugaring Evaluation Sequences

Tags: Programming Languages, Resugaring, Semantics, Visualization

Posted on 06 February 2016.

This is the first post in a series about resugaring. It focuses on resugaring evaluation sequences. See also our later posts on resugaring scope rules and resugaring type rules.

A lot of programming languages are defined in terms of syntactic sugar. This has many advantages, but also a couple of drawbacks. In this post, I’m going to tell you about one of these drawbacks, and the solution we found for it. First, though, let me describe what syntactic sugar is and why it’s used.

Syntactic sugar is when you define a piece of syntax in a language in terms of the rest of the language. You’re probably already familiar with many examples. For instance, in Python, x + y is syntactic sugar for x.__add__(y). I’m going to use the word “desugaring” to mean the expansion of syntactic sugar, so I’ll say that x + y desugars to x.__add__(y). Along the same lines, in Haskell, [f x | x <- lst] desugars to map f lst. (Well, I’m simplifying a little bit; the full desugaring is given by the Haskell 98 spec.)

As a programming language researcher I love syntactic sugar, and you should too. It splits a language into two parts: a big “surface” language that has the sugar, and a much smaller “core” language that lacks it. This separation lets programmers use the surface language that has all of the features they know and love, while letting tools work over the much simpler core language, which lets the tools themselves be simpler and more robust.

There’s a problem, though (every blog post needs a problem). What happens when a tool, which has been working over the core language, tries to show code to the programmer, who has been working over the surface? Let’s zoom in on one instance of this problem. Say you write a little snippet of code, like so: (This code is written in an old version of Pyret; it should be readable even if you don’t know the language.)

my-list = [2]
cases(List) my-list:
  | empty() => print("empty")
  | link(something, _) =>
    print("not empty")
end

And now say you’d like to see how this code runs. That is, you’d like to see an evaluation sequence (a.k.a. an execution trace) of this program. Or maybe you already know what it will do, but you’re teaching students, and would like to show them how it will run. Well, what actually happens when you run this code is that it is first desugared into the core, like so:

my-list = list.["link"](2, list.["empty"])
block:
  tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({
    "empty" : fun(): print("empty") end,
    "link" : fun(something, _):
      print("not empty") end
},
fun(): raise("cases: no cases matched") end)
end

This core code is then run (each block of code is the next evaluation step):

my-list = obj.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = obj.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, obj.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, obj.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, [])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = [2]
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

tempMODRIOUJ :: List = [2]
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)

[2].["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)

[2].["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)

<func>({"empty" : fun(): end, "link" : fun(something, _): print("not
empty") end}, fun(): raise("cases: no cases matched") end)

<func>({"empty" : fun(): end, "link" : fun(): end}, fun():
raise("cases: no cases matched") end)

<func>(obj, fun(): raise("cases: no cases matched") end)

<func>(obj, fun(): end)

<func>("not empty")

"not empty"

But that wasn’t terribly helpful, was it? Sometimes you want to see exactly what a program is doing in all its gory detail (along the same lines, it’s occasionally helpful to see the assembly code a program is compiling to), but most of the time it would be nicer if you could see things in terms of the syntax you wrote the program with! In this particular example, it would be much nicer to see:

my-list = [2]
cases(List) my-list:
  | empty() => print("empty")
  | link(something, _) =>
    print("not empty")
end

my-list = [2]
cases(List) my-list:
  | empty() => print("empty")
  | link(something, _) =>
    print("not empty")
end

cases(List) [2]:
| empty() => print("empty")
| link(something, _) =>
  print("not empty")
end

<func>("not empty")

"not empty"

(You might have noticed that the first step got repeated for what looks like no reason. What happened there is that the code [2] was evaluated to an actual list, which also prints itself as [2].)

So we built a tool that does precisely this. It turns core evaluation sequences into surface evaluation sequences. We call the process resugaring, because it’s the opposite of desugaring: we’re adding the syntactic sugar back into your program. The above example is actual output from the tool, for an old version of Pyret. I’m currently working on a version for modern Pyret.

Resugaring Explained

I always find it helpful to introduce a diagram when explaining resugaring. On the right is the core evaluation sequence, which is the sequence of steps that the program takes when it actually runs. And on the left is the surface evaluation sequence, which is what you get when you try to resugar each step in the core evaluation sequence. As a special case, the first step on the left is the original program.

Here’s an example. The starting program will be not(true) or true, where not is in the core language, but or is defined as a piece of sugar:

x or y    ==desugar==>  let t = x in
                          if t then t else y

And here’s the diagram:

The steps (downarrows) in the core evaluation sequence are ground truth: they are what happens when you actually run the program. In contrast, the steps in the surface evaluation sequence are made up; the whole surface evaluation sequence is an attempt at reconstructing a nice evaluation sequence by resugaring each of the core steps. Notice that the third core term fails to resugar. This is because there’s no good way to represent it in terms of or.

Formal Properties of Resugaring

It’s no good to build a tool without having a precise idea of what it’s supposed to do. To this end, we came up with three properties that (we think) capture exactly what it means for a resugared evaluation sequence to be correct. It will help to look at the diagram above when thinking about these properties.

Emulation says that every term on the left should desugar to the term to its right. This expresses the idea that the resugared terms can’t lie about the term they’re supposed to represent. Another way to think about this is that desugaring and resugaring are inverses.
Abstraction says that the surface evaluation sequence on the left should show a sugar precisely when the programmer used it. So, for example, it should show things using or and not let, because the original program used or but not let.
Coverage says that you should show as many steps as possible. Otherwise, technically the surface evaluation sequence could just be empty! That would satisfy both Emulation and Abstraction, which only say things about the steps that are shown.

We’ve proved that our resugaring algorithm obeys Emulation and Abstraction, and given some good emperical evidence that it obeys Coverage too.

I’ve only just introduced resugaring. If you’d like to read more, see the paper, and the followup that deals with hygiene (e.g., preventing variable capture).

Slimming Languages by Reducing Sugar

Tags: JavaScript, Programming Languages, Resugaring, Semantics

Posted on 08 January 2016.

JavaScript is a crazy language. It’s defined by 250 pages of English prose, and even the parts of the language that ought to be simple, like addition and variable scope, are very complicated. We showed before how to tackle this problem using λ_s5, which is an example of what’s called a tested semantics.

You can read about λ_s5 at the above link. But the basic idea is that λ_s5 has two parts:

A small core language that captures the essential parts of JavaScript, without all of its foibles, and
A desugaring function that translates the full language down to this small core.

(We typically call this core language λ_s5, even though technically speaking it’s only part of what makes up λ_s5.)

These two components together give us an implementation of JavaScript: to run a program, you desugar it to λ_s5, and then run that program. And with this implementation, we can run JavaScript’s conformance test suite to check that λ_s5 is accurate: this is why it’s called a tested semantics. And lo, λ_s5 passes the relevant portion of the test262 conformance suite.

The Problem

Every blog post needs a problem, though. The problem with λ_s5 lies in desugaring. We just stated that JavaScript is complicated, while the core language for λ_s5 is simple. This means that the complications of JavaScript must be dealt with not in the core language, but instead in desugaring. Take an illustrative example. Here’s a couple of innocent lines of JavaScript:

function id(x) {
    return x;
}

These couple lines desugar into the following λ_s5 code:

{let
 (%context = %strictContext)
 { %defineGlobalVar(%context, "id");
  {let
   (#strict = true)
   {"use strict";
    {let
     (%fobj4 =
       {let
         (%prototype2 = {[#proto: %ObjectProto,
                          #class: "Object",
                          #extensible: true,]
                         'constructor' : {#value (undefined) ,
                                          #writable true ,
                                          #configurable false}})
         {let
          (%parent = %context)
          {let
           (%thisfunc3 =
             {[#proto: %FunctionProto,
               #code: func(%this , %args)
                     { %args[delete "%new"];
                       label %ret :
                       { {let
                          (%this = %resolveThis(#strict,
                                                %this))
                          {let
                           (%context =
                             {let
                               (%x1 = %args
                                        ["0" , null])
                               {[#proto: %parent,
                                 #class: "Object",
                                 #extensible: true,]
                                'arguments' : {#value (%args) ,
                                         #writable true ,
                                         #configurable false},
                                'x' : {#getter func
                                         (this , args)
                                         {label %ret :
                                         {break %ret %x1}} ,
                                       #setter func
                                         (this , args)
                                         {label %ret :
                                         {break %ret %x1 := args
                                         ["0" , {[#proto: %ArrayProto,
                                         #class: "Array",
                                         #extensible: true,]}]}}}}})
                           {break %ret %context["x" , {[#proto: null,
                                                  #class: "Object",
                                                  #extensible: true,]}];
                            undefined}}}}},
               #class: "Function",
               #extensible: true,]
              'prototype' : {#value (%prototype2) ,
                             #writable true ,
                             #configurable true},
              'length' : {#value (1.) ,
                          #writable true ,
                          #configurable true},
              'caller' : {#getter %ThrowTypeError ,
                          #setter %ThrowTypeError},
              'arguments' : {#getter %ThrowTypeError ,
                             #setter %ThrowTypeError}})
           { %prototype2["constructor" = %thisfunc3 , null];
             %thisfunc3}}}})
     %context["id" = %fobj4 ,
              {[#proto: null, #class: "Object", #extensible: true,]
               '0' : {#value (%fobj4) ,
                      #writable true ,
                      #configurable true}}]}}}}}

This is a bit much. It’s hard to read, and it’s hard for tools to process. But more to the point, λ_s5 is meant to be used by researchers, and this code bloat has stood in the way of researchers trying to adopt it. You can imagine that if you’re trying to write a tool that works over λ_s5 code, and there’s a bug in your tool and you need to debug it, and you have to wade through that much code just for the simplest of examples, it’s a bit of a nightmare.

The Ordinary Solution

So, there’s too much code. Fortunately there are well-known solutions to this problem. We implemented a number of standard compiler optimization techniques to shrink the generated λ_s5 code, while preserving its semantics. Here’s a boring list of the Semantics-Preserving optimizations we used:

Dead-code elimination
Constant folding
Constant propogation
Alias propogation
Assignment conversion
Function inlining
Infer type & eliminate static checks
Clean up unused environment bindings

Most of these are standard textbook optimizations; though the last two are specific to λ_s5. Anyhow, we did all this and got… 5-10% code shrinkage.

The Extraordinary Solution

That’s it: 5-10%.

Given the magnitude of the code bloat problem, that isn’t nearly enough shrinkage to be helpful. So let’s take a step back and ask where all this bloat came from. We would argue that code bloat can be partitioned into three categories:

Intended code bloat. Some of it is intentional. λ_s5 is a small core language, and there should be some expansion as you translate to it.
Incidental code bloat. The desugaring function from JS to λ_s5 is a simple recursive-descent function. It’s purposefully not clever, and as a result it sometimes generates redundant code. And this is exactly what the semantics-preserving rewrites we just mentioned get rid of.
Essential code bloat. Finally, some code bloat is due to the semantics of JS. JS is a complicated langauge with complicated features, and they turn into complicated λ_s5 code.

There wasn’t much to gain by way of reducing Intended or Incidental code bloat. But how do you go about reducing Essential code bloat? Well, Essential bloat is the code bloat that comes from the complications of JS. To remove it, you would simplify the language. And we did exactly that! We defined five Semantics-Altering transformations:

(IR) Identifier restoration: pretend that JS is lexically scoped
(FR) Function restoration: pretend that JS functions are just functions and not function-object-things.
(FA) Fixed arity: pretend that JS functions always take as many arguments as they’re declared with.
(UAE) Assertion elimination: unsafely remove some runtime checks (your code is correct anyways, right?)
(SAO) Simplifying arithmetic operators: eliminate strange behavior for basic operators like “+”.

These semantics-altering transformations blasphemously break the language. This is actually OK, though! The thing is, if you’re studying JS or doing static analysis, you probably already aren’t handling the whole language. It’s too complicated, so instead you handle a sub-language. And this is exactly what these semantics-altering transformations capture: they are simplifying assumptions about the JS language.

Lessons about JavaScript

And we can learn about JavaScript from them. We implemented these transformations for λ_s5, and so we could run the test suite with the transformations turned on and see how many tests broke. This gives a crude measure of “correctness”: a transformation is 50% correct if it breaks half the tests. Here’s the graph:

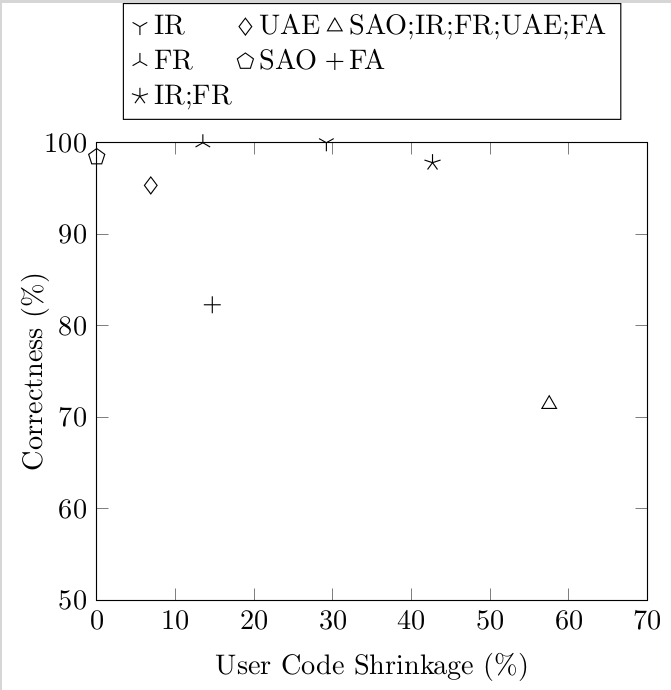
Notice that the semantics-altering transformations shrink code by more than 50%: this is way better than the 5-10% that the semantics-preserving ones gave. Going back to the three kinds of code bloat, this shows that most code bloat in λ_s5 is Essential: it comes from the complicated semantics of JS, and if you simplify the semantics you can make it go away.

Next, here’s the shrinkages of each of the semantics-altering transformations:

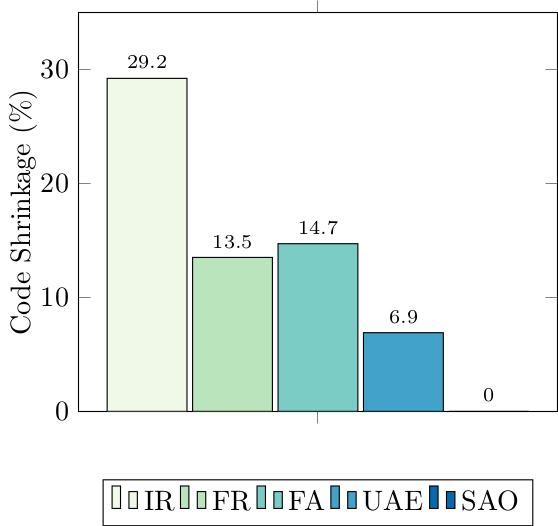
Since these semantics-altering transformations are simplifications of JS semantics, and desugared code size is a measure of complexity, you can view this graph as a (crude!) measure of complexity of language features. In this light, notice IR (Identifier Restoration): it crushes the other transformations by giving 30% code reduction. This shows that JavaScript’s scope is complex: by this metric 30% of JavaScript’s complexity is due to its scope.

Takeaway

These semantics-altering transformations give semantic restrictions on JS. Our paper makes these restrictions precise. And they’re exactly the sorts of simplifying assumptions that papers need to make to reason about JS. You can even download λ_s5 from git and implement your analysis over λ_s5 with a subset of these restrictions turned on, and test it. So let’s work toward a future where papers that talk about JS say exactly what sub-language of JS they mean.

The Paper

This is just a teaser: to read more, see the paper.

The Brown PLT Blog