Articles by tag: Higher-Order Functions
Structural Versus Pipeline Composition of Higher-Order Functions
Plan Composition Using Higher-Order Functions
Adding Function Transformers to CODAP
Developing Behavioral Concepts of Higher-Order Functions
Observations on the Design of Program Planning Notations for Students
Tags: Higher-Order Functions, Education, Program Planning, User Studies
Posted on 27 December 2023.In two recent projects we’ve tried to make progress on the long-dormant topic of teaching students how to plan programs. Concretely, we chose higher-order functions as our driving metaphor to address the problem of “What language shall we use to express plans?” We showed that this was a good medium for students. We also built some quite nice tool support atop Snap!. Finally, we were making progress on this long open issue!
Not so fast.
We tried to replicate our previous finding with a new population of students and somewhat (but not entirely) different problems. It didn’t work well at all. Students made extensive complaints about the tooling and, when given a choice, voted with their feet by not using it.
We then tried again, allowing them freedom in what notation they used, but suggesting two: one was diagrammatic (essentially representing dataflow), and the other was linear prose akin to a todo-list or recipe. Students largely chose the latter, and also did a better job with planning.
Overall, this is a sobering result. It diminishes some of our earlier success. At the same time, it sheds more light on the notations students prefer. In particular, it returns to our earlier problem: planning needs a vocabulary, and we are still far from establishing one that students find comfortable and can use successfully. But it also highlights deeper issues, such as the need to better support students with composition. Critically, composition serves as a bridge between more plan-oriented students and bricoleurs, making it especially worthy of more study, no matter your position on how students should or do design programs.
For more details, see the paper.
Structural Versus Pipeline Composition of Higher-Order Functions
Tags: Higher-Order Functions, Education, User Studies
Posted on 16 August 2022.Building on our prior work on behavioral conceptions of higher-order functions (HOFs), we have been looking now at their composition. In designing a study, we kept running into tricky problems in designing HOF composition problems. Eventually, we set out to study that question directly.
We’re going to give you a quiz. Imagine you have a set of standard
HOFs (map, filter, sort, andmap, ormap, take-while). You
are given two ways to think about composing them (where “funarg” is
short for the parameter that is a function):
Type A: HOF_A(<some funarg>, HOF_B(<some funarg>, L))
Type B: HOF_C((lambda (inner) HOF_D(<some funarg>, inner)), L)
-
Which of these would you consider “easier” for students to understand and use?
-
How would you rate their relative expressive power in terms of problems they can solve?
Don’t go on until you’ve committed to answers to these questions.
Rather than A and B, here are better names: we’ll refer to A
as pipeline, because it corresponds to a traditional
data-processing/Unix pipeline composition (HOF_B L | HOF_A), and
we’ll refer to B as structural. If you’re like many other people
we’ve asked, you likely think that pipeline is easier, but you’re less
certain about how to answer the second question.
Alright, now you’re ready to read the paper! We think the structural/pipeline distinction is similar to the structural/generative recursion distinction in HtDP, and similarly has consequences for how we order HOF composition in our pedagogy. We discuss all this, and more, in the document.
Plan Composition Using Higher-Order Functions
Tags: Higher-Order Functions, Education, Program Planning, User Studies
Posted on 09 July 2022.There is a long history of wanting to examine planning in computing education research, but relatively little work on it. One problem you run into when trying to do this seriously is: “What language shall we use to express plans?” A lot hinges on this language.
-
The programming language itself is too low-level: there are too many administrative details that get in the way and might distract the student; failures may then reflect these distractions, not an inability to plan.
-
Plain English may be too high-level. It’s both difficult to give any useful (automated) feedback about, it may also require too much interpretation. In particular, an expert may interpret student utterances in ways the student didn’t mean, thereby giving the student an OK signal when in fact the student is not on the right path.
Separately, in prior work, we looked at whether students are able to understand higher-order functions (HOFs) from a behavioral perspective: i.e., as atomic units of behavior without reference to their underlying implementation. For our population, we found that they generally did quite well.
You may now see how these dovetail. Once students have a behavioral understanding of individual HOFs, you can use them as a starting vocabulary for planning. Or to think in more mechanical terms, we want to study how well students understand the composition of HOFs. That is the subject of this work.
Concretely, we start by confirming our previous result—that they understand the building blocks—and can also articulate many of the features that we previously handed out to them. This latter step is important because any failures at composition may lie in their insufficiently rich understanding of the functions. Fortunately, we see that this is again not a problem with our population.
We then focus on the main question: can they compose these HOFs. We do this in two ways:
-
We give them input-output examples and ask them to identify which compositions of functions would have produced those results. This is akin to having a dataset you need to transform and knowing what you would like the result to look like, and figuring out what steps will take it there.
-
We give them programming problems to solve, and ask them to first provide high-level plans of their solutions.
What we find is that students don’t do superbly on (1), but do extremely well on (2). Indeed, our goal had been to study what changes between the planning and programming phase (e.g., if they planned incorrectly but programmed correctly; or vice versa), but our students unfortunately did too well on both to give us any useful data!
Of particular interest is how we got them to state plans. While HOFs are the “semantics”, we still need a “syntax” for writing them. Conventional textual programming has various bad affordances. Instead, we created a custom palette of operations in Snap!. In keeping with the point of this paper, the operations were HOFs. There are numerous advantages to this use of Snap!:
-
Drag-and-drop construction avoids getting bogged down in the vagaries of textual syntax.
-
Changing plans is much easier, because you can drag whole blocks and (again) not get caught up in messy textual details. This means students are hopefully more willing to change around their plans.
-
The planning operations focus on the operations we care about, and students can ignore irrelevant details.
-
Most subtly: the blanks can be filled in with text. That is, you get “operations on the outside, text on the inside”: at the point where things get too detailed, students can focus on presenting their ideas rather than on low-level details. This is, in other words, a hybrid of the two methods we suggested at the beginning.
Critically, these aren’t programs! Because of the text, they can’t be executed. But that’s okay! They’re only meant to help students think through their plans before starting to write the program. In particular, given students’ reluctance to change their programs much once they start coding, it seems especially important to give them a fluid medium—where switching costs are low—in which to plan things before they start to write a line of code. So one of the best things about this paper, beyond the main result, is actually our discovery of Snap!’s likely utility in this setting.
For more details, see the paper!
Adding Function Transformers to CODAP
Tags: Higher-Order Functions, Education, Tables, Tools
Posted on 22 August 2021.CODAP is a wonderful tool for data transformation. However, it also has important limitations, especially from the perspective of our curricula. So we’ve set about addressing them so that we can incorporate CODAP into our teaching.
CODAP
We at Brown PLT and Bootstrap are big fans of CODAP, a data-analysis tool from the Concord Consortium. CODAP has very pleasant support for working with tables and generating plots, and we often turn to it to perform a quick analysis and generate a graph.
One of the nice things about CODAP, that sets it apart from traditional spreadsheets, is that the basic unit of space is not a table or spreadsheet but a desktop that can contain several objects on it. A workspace can therefore contain many objects side-by-side: a table, a graph, some text, etc.:
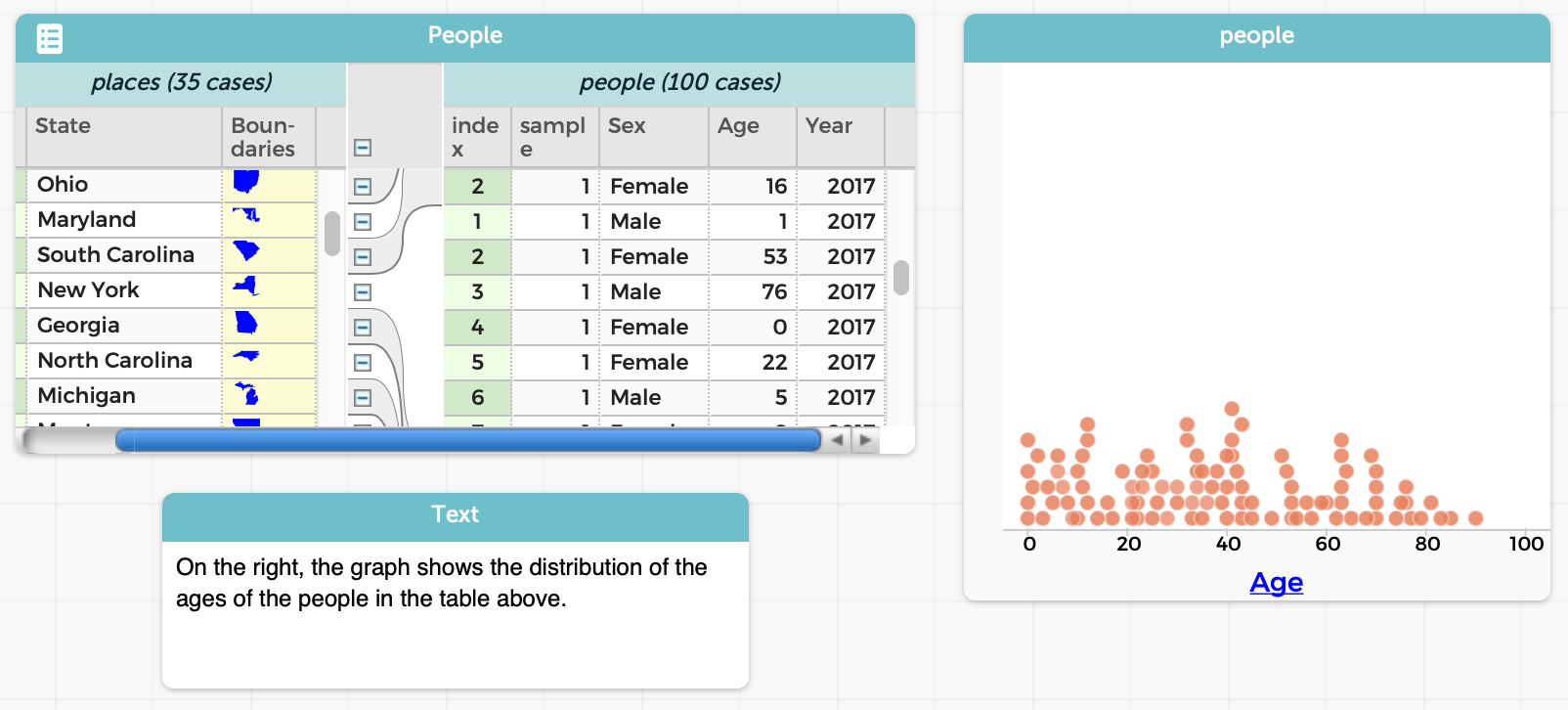
Also, a lot of things in CODAP are done through direct manipulation. This is helpful for younger students, who may struggle with formal programming but can use a GUI to manipulate objects.
There are many other nice features in CODAP, such as the ability to track a data case cross representations, and so on. We urge you to go try it out! When you launch a new CODAP instance, CODAP will offer you a folder of examples, which can help you get acquainted with it and appreciate its features.
What’s Not to Love?
Unfortunately, we don’t love everything about CODAP. We’ll illustrate with an example. To be clear, this is not a bug in CODAP, but rather an important difference of opinion in ease-of-use.
Let’s say we want to find all the people who are below 50 years of age. In CODAP, there are a few ways to do it, all of which have their issues.
If you don’t mind being imprecise (which may be okay for a quick data exploration, but isn’t if you want to, say, compute a statistic over the result):
- Create a new graph.
- Drag the
Agecolumn to the graph. - Select all the items that are under 50 using visual inspection. (Depending on how much data you have and their spread, you’ll quite possibly under- and/or over-shoot.)
- Then do the last few steps below.
If you care to get an accurate selection, instead begin with:
- First, add a new column to the original table.
- Enter a formula for that column (in this case,
Age < 50). - Obtain a selection of the desired items, which can be done in several different ways, also all with trade-offs:
-
Sort by that column. Unfortunately, this won’t work if there’s grouping in the table. You’d have to select manually. (Try it. This may be a bit harder than it seems.)
-
Create a graph as above, but of the new column. This will give you a clean separation into two values. Manually select all the values in the
truecolumn. At least now it will be visually clear if you didn’t select all the right values (if the dataset is not too large). -
Remove the formula for the new column. Now drag it to the leftmost end of the table. (If you don’t remove the formula, you’ll get an error!) Now you have all the elements grouped by
trueandfalse(and operations performed to one can also be performed to the other).
You’re not done! You still have more steps to go:
- If you aren’t already in the table (e.g., if you made a graph), select the table.
- Click on the “Eye” icon.
- Choose the “Set Aside Unselected Cases” entry.
Note that, in most or all of these cases:
- You’ve added a completely superfluous column to your dataset.
- You may have changed the order of items in your dataset.
- You’ve lost the ability to see the original data alongside the filtered data.
- You had to take numerous steps.
- You had to remember to use the Eye icon for filtering, as opposed to other GUI operations for other tasks.
- You had to remember where the Eye icon even is: it’s hidden when a table isn’t selected.
But most of all, in every single case:
- You had to perform all these operations manually.
Why does this matter? We need data science to be reproducible: we should be able to give others our datasets and scripts so they can re-run them to check that they get the same answer, tweak them so they can check the robustness of our answers, and so on. But when all the operations are done manually, there’s no “script”, only output. That focuses on answers rather than processes, and is anti-reproducibility.
In contrast, we think of filtering as a program operation that we apply to a table to produce a new table, leaving the original intact: e.g., the way it works in Pyret. This addresses almost all of the issues above.
Other Pedagogic Consequences
CODAP had to make certain design choices. They made good choices for some settings: for younger children, in particular, the direct manipulation interface works very nicely. It’s a low floor. However, we feel it’s also a lower-than-we’d-like ceiling. There are many things that the CODAP view of data transformation inhibits:
- Making operations explicit, as we noted above.
- Introducing the idea of functions or transformations of data as objects in their own right, not only as manual operations.
- Having explicit data-transformation functions also connects to other related school curricula, such as algebra.
- Saving and naming repeated operations, to learn a bottom-up process of developing abstractions.
- Examining old and new tables side-by-side.
This last point is especially important. A critical task in data science is performing “what if” analyses. What-if fundamentally means we should be able to perform some operation (the “if” part) and compare the output (the “what” part). We might even want to look at multiple different scenarios, representing different possible outcomes. But traditional what-if analysis, whether in CODAP or on spreadsheets, often requires you, the human, to remember what has changed, rather than letting the computer do it for you. (Microsoft Excel has limited support to get around this, but its very presence indicates that spreadsheets, traditionally, did not support what-if analysis—even though that’s how they have often been marketed.)
Finally, there’s also a subtle consequence to CODAP’s design: derived tables must look substantially similar to their parents. In computing terms, the schema should be largely the same. That works fine when an operation has little impact on the schema: filtering doesn’t change the schema at all (in principle, though in CODAP you have to add an extra column…), and adding a new column is a conservative extension. But what if you want to perform an operation that results in a radically different schema? For instance, consider the “pivot wider” and “pivot longer” operations when we create tidy data. The results of those operations have substantially different schemas!
Introducing CODAP Transformers
In response to this critique, we’ve added a new plugin to CODAP called Transformers:
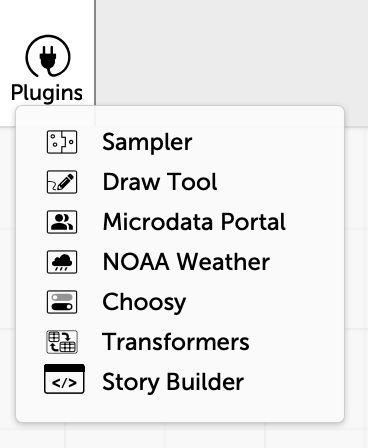
(This work was done by undergrad trio Paul Biberstein, Thomas Castleman, and Jason Chen.)
This introduces a new pane that lists several transformation operations, grouped by functionality:
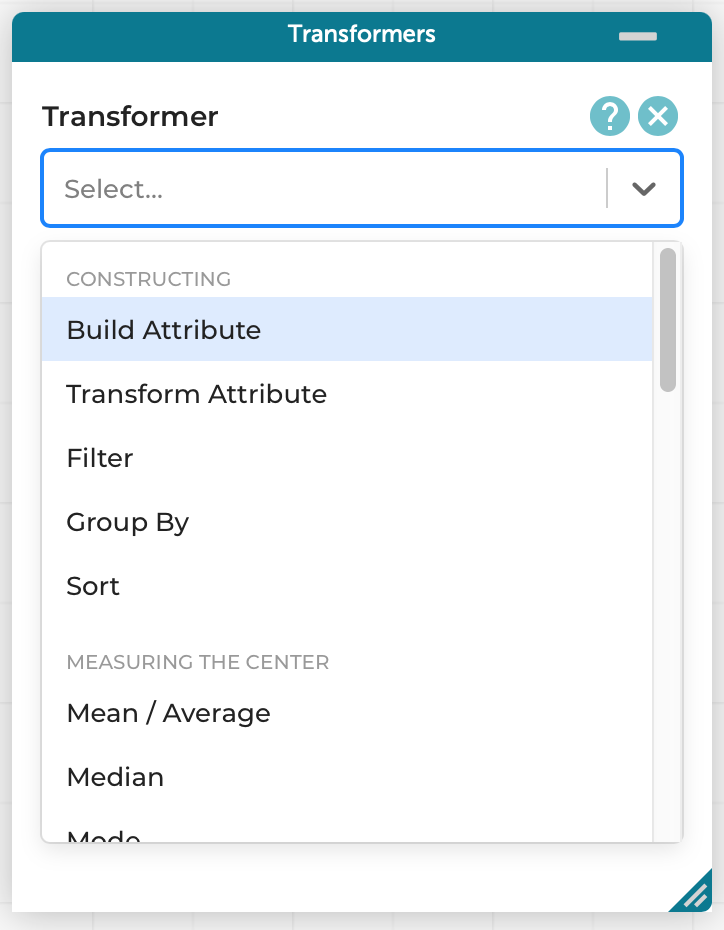
For instance, with no more textual programming than before (the formula is the same), we can perform our same example as before, i.e., finding all the people younger than 50:
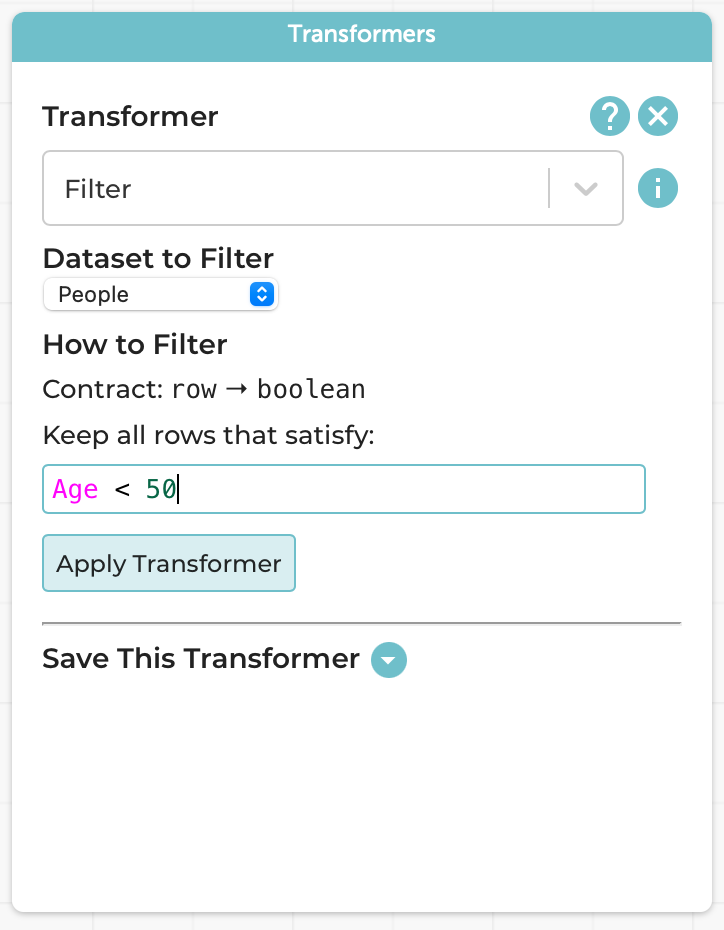
The result is a new table, which co-exists with the original:
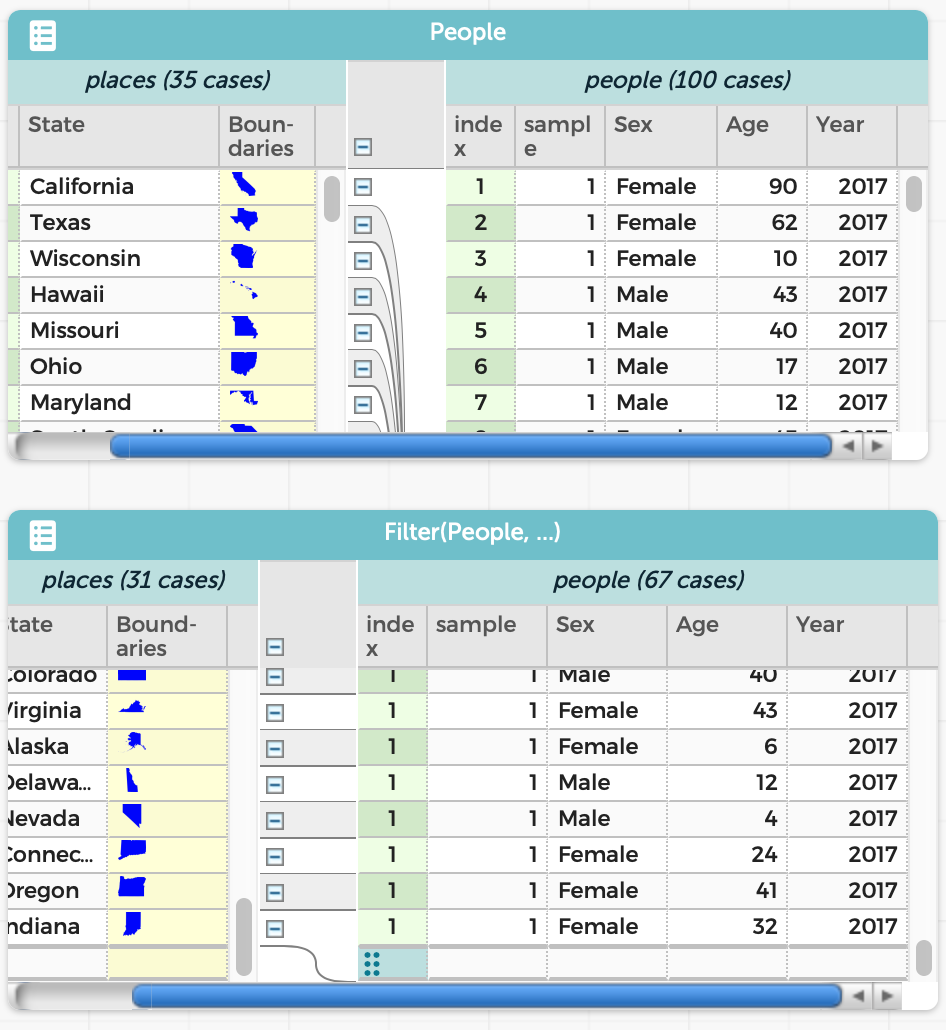
The resulting table is just as much a table as the original. For instance, we can graph the ages in the two tables and see exactly the difference we’d expect:
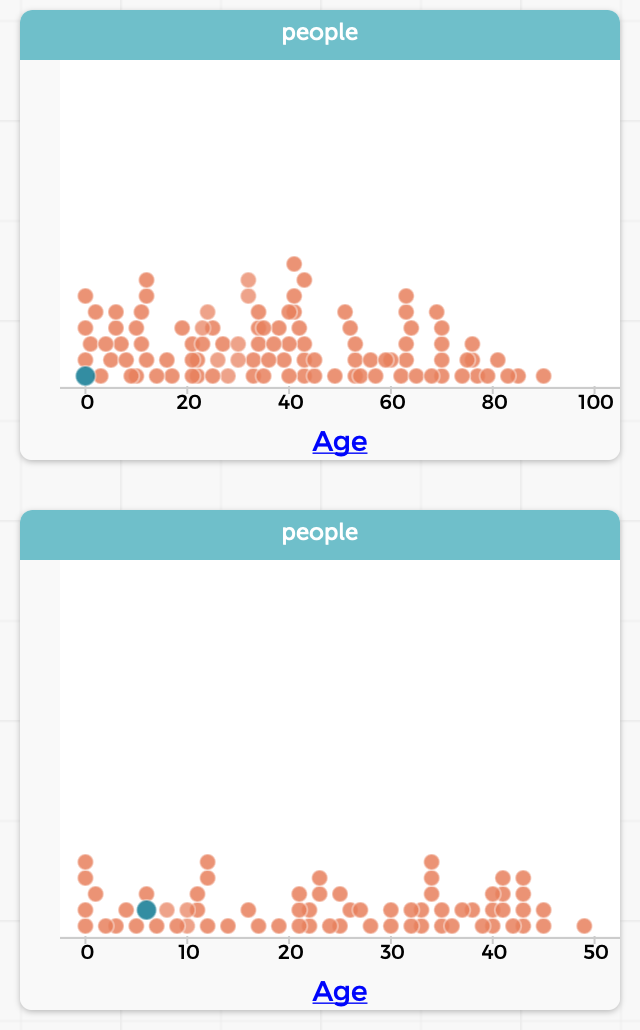
(Over time, of course, you may build up many tables. The Transformers plugin chooses names based on the operations, to make them easy to tell apart. CODAP also lets you resize, minimize, and delete tables. In practice, we don’t expect users to have more than 3–4 tables up at a time.)
Saving Transformers
We might want to perform the same operation on multiple tables. This is valuable in several contexts:
-
We create a hand-curated table, with known answers, as a test case to make sure our operations perform what we expect. After confirming this, we want to be sure that we applied the exact same operation to the real dataset.
-
We want to perform the same operation to several related datasets: e.g., a table per year.
We might also simply want to give a meaningful name to the operation.
In such cases, we can use the “Save This Transformer” option at the bottom of the Transformers pane:
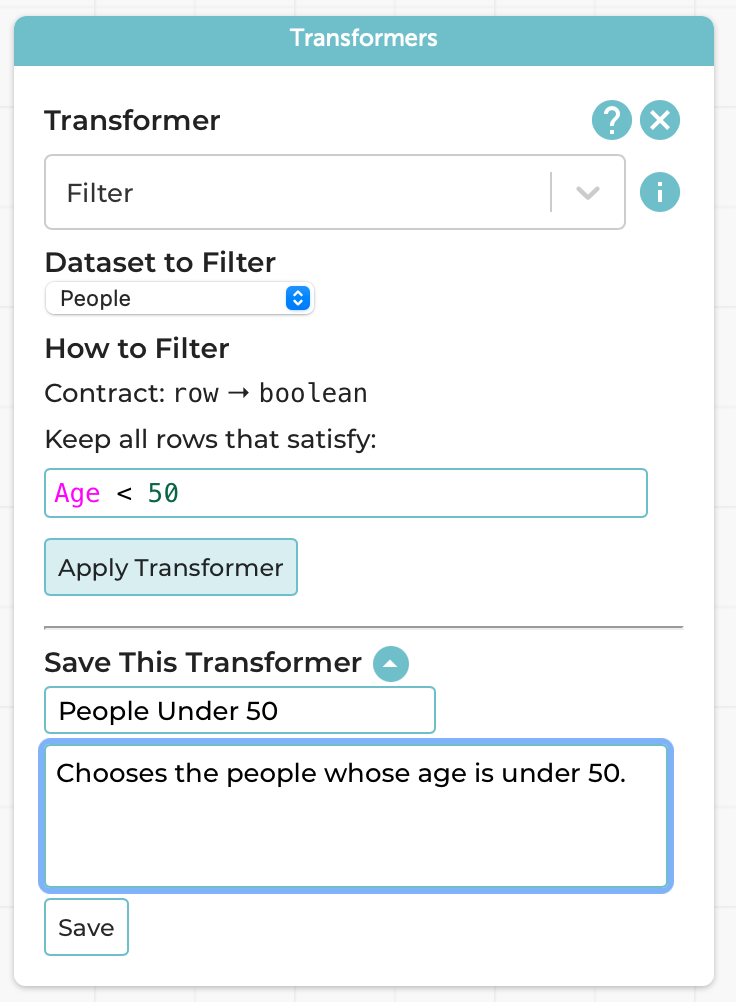
Following the programming processes we follow and teach, we naturally want you to think about the Design Recipe steps when saving it because, in programming terms, you’re creating a new function.
This now creates a new named transformer:
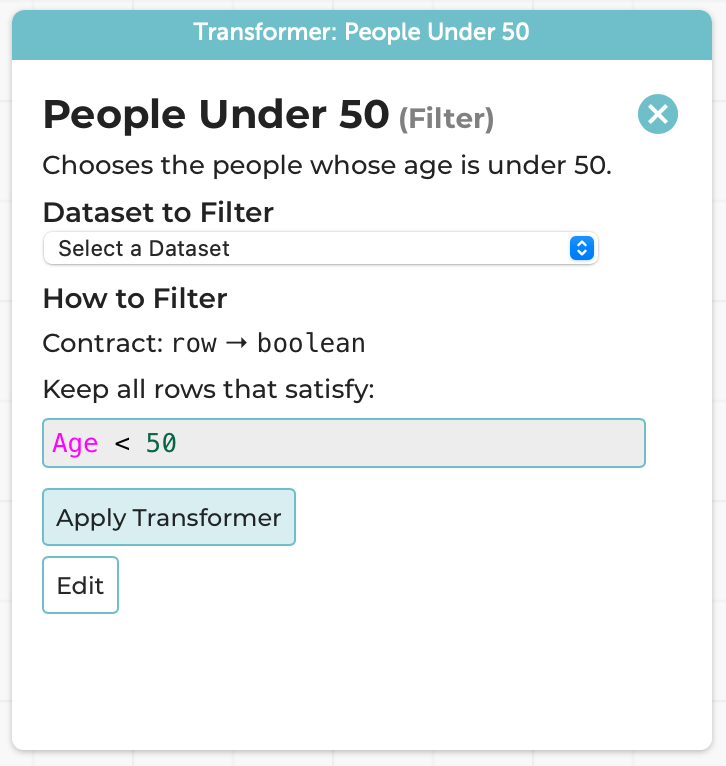
Every part of this is frozen other than the choice of dataset; it can be applied as many times as you want, to as many datasets as you want. The above use-cases are suggestions, but you can use it however you wish.
A Note on Errors
Suppose you try to apply an operation improperly. Say, for instance, you have a table of people that does not have an Age column, and you try to filter people with Age < 50. There are at least two choices that Transformers can take:
-
Allow you to try to perform the operation, and report an error.
-
Prevent you from even trying by simply not showing tables that are invalid in the drop-down list of tables that the operation can be applied to.
We know exactly what the programming languages reader reading this is thinking: “You’re going to choose the latter, right? Right?!? PLEASE TELL ME YOU ARE!!!”
Gentle Reader: we’re not.
Here’s why we chose not to.
- There’s the messy implementation detail of figuring out exactly when a table should or shouldn’t be shown in the drop-down. And we’d have to maintain that across changes to the CODAP language. There are no such problems in the dynamic version.
But hey, we’re language implementors, we can figure these things out. Rather, our real reason comes from human factors:
- Imagine you’re a teacher with a classroom full of students. A student tries to apply an operation to the wrong table. They probably don’t even realize that the operation can’t be applied. All they know is that the table doesn’t appear in the list. Their table doesn’t appear in the list! Their reaction is (perhaps rightly) going to be to raise their hand and say to their teacher, “This tool is broken! It won’t even show me my table!!!” And the teacher, dealing with a whole bunch of students, all in different states, may not immediately realize why the table doesn’t show. Everyone’s frustrated; the student feels stuck, and the teacher may be left feeling inadequate.
In contrast, if we just let the operation happen, here’s what the student sees:

Now the student has a pretty good chance of figuring out for themselves what went wrong: not pulling away the teacher from helping someone else, not blaming the tool, and instead giving themselves a chance of fixing their own problem.
There’s potentially a broader lesson here about making invalid states unrepresentable. Potentially.
Many, Many Transformers!
We’ve focused on just one transformation here. There are many more. We even have the pivoting operations for tidy data! (It would have been wrong to tease you with that up top, otherwise.)
We even take the what-if part seriously: the Compare Transformer lets you compare numeric and categorical data. Believe it or not, the categorical comparison operator was actually inspired by prior work we’ve done for many years on comparing access control policies, router configurations, and SDN programs (see also our two brief position papers). It’s pretty thrilling to see the flow of ideas from security and networking research to data science education in a small but very non-obvious way: the grouping in the categorical output is directly inspired by the multi-terminal decision diagrams of our original Margrave system. For more on this line of work, see our blog post.
Examples
For your benefit, we’ve set up a bunch of pre-built CODAP examples that show you the operations in action:
- Building attributes, Filtering, and Updating data
- Partition
- Filter, Running Sum, and their interaction
- Transformers that produce single values
- Reusing saved transformers
- Categorical Compare
- Numerical Compare
- Pivot operations from tidy data
Make Your Own!
As you might have guessed from the examples above, transformers are now part of the official CODAP tool. You can go play with them right now on the CODAP site. Have fun! Tell us what you learned.
Thanks
Special thanks to our friends at the Concord Consortium, especially William Finzer, Jonathan Sandoe, and Chad Dorsey, for their support.
Developing Behavioral Concepts of Higher-Order Functions
Tags: Higher-Order Functions, Education, User Studies
Posted on 31 July 2021.Higher-Order Functions (HOFs) are an integral part of the programming process. They are so ubiquitous, even Java had to bow and accept them. They’re especially central to cleanly expressing the stages of processing data, as the R community and others have discovered.
How do we teach higher-order functions? In some places, like
How to Design Programs,
HOFs are presented as abstractions over common patterns. That is,
you see a certain pattern of program behavior over and over, and
eventually learn to parameterize it and call it map, filter, and
so on. That is a powerful method.
In this work, we take a different perspective. Our students often write examples first, so they can think in terms of the behavior they want to achieve. Thus, they need to develop an understanding of HOFs as abstractions over common behaviors: “mapping”, “filtering”, etc.
Our goal in this work is to study how well students form behavioral abstractions having been taught code pattern abstractions. Our main instrument is sets of input-output behavior, such as
(list "red" "green" "blue")
-->
(list 3 5 4)
(Hopefully that calls to mind “mapping”.) We very carefully designed a set of these to capture various specific similarities, overlaps, and impossibilities.
We then evaluated students using two main devices, inspired by activities in machine learning:
-
Clustering: Group behaviors into clusters of similar ones.
-
Classification: For each behavior, assign a label.
We also tried labeling over visual presentations.
Our paper describes these instruments in detail, and our outcomes. What is most interesting, perhaps, is not our specific outcomes, but this style of thinking about teaching HOFs. We think the materials—especially the input-output pairs, and a table of properties—will be useful to educators who are tackling this topic. More broadly, we think there’s a huge unexplored space of HOF pedagogy combined with meaningful evaluation. We hope this work inspires more work along these lines.
