Mechanized LambdaJS
Tags: JavaScript, Programming Languages, Semantics
Posted on 04 June 2012.See the discussion on Lambda the Ultimate about this work.
In an earlier post, we introduced λJS, our operational semantics for JavaScript. Unlike many other operational semantics, λJS is no toy, but strives to correctly model JavaScript's messy details. To validate these claims, we test λJS with randomly generated tests and with portions of the Mozilla JavaScript test suite.
Testing is not enough. Despite our work, other researchers found a missing case in λJS. Today, we're introducing Mechanized λJS, which comes with a machine-checked proof of correctness, using the Coq proof assistant.
Recap: The Structure of λJS
λJS has two key parts: an operational semantics and a desugaring function. Our earlier post discusses how we tackle the minutiae of JavaScript with our desugaring function. This post focuses on the operational semantics, where others found a bug, which now has a machine-checked proof of correctness.
The operational semantics is typical of programming languages research. It specifies the sequence of steps required to evaluate the program. For example, the following sequence evaluates to a value:
{ x: 2 + 3, y : 9 }["x"] * (11 + 23)
→ { x: 5, y: 9 }["x"] * (11 + 23)
→ 5 * (11 + 23)
→ 5 * 34
→ 170
The sequence above evaluates expressions from left to right—a detail
spelled out in the operational semantics.
Not all expressions reduce to values. For example, the following reduces to an error:
null["x"] → err "Cannot read property 'x' of null"An operational semantics specifies exactly which errors may occur.
Finally, an operational semantics allows some programs to run forever. This is a basic infinite loop, and its non-terminating reduction sequence:
while (true) { 1; }
→ if true then 1; while (true) { 1; } else undefined
→ 1; while (true) { 1; }
→ while (true) { 1; }
→ if true then 1; while (true) { 1; } else undefined
→ 1; while (true) { 1; }
…
In general, these are the only three cases that the semantics should allow—an expression must either (1) evaluate to a value, (2) signal an error, or (3) not terminate. In fact, we can state that as a theorem.
Theorem 1 (Soundness). For all λJS programs, p, either:
- p →* v,
- p →* err, or
- p →* p2, and there exists a p3 such that p2 → p3.
This is a standard theorem worth proving for any language. Since languages and their correctness proofs involve detailed, delicate designs and decisions, the proofs are easy to do wrong, and tedious for humans to get right. If only computers could help.
PLT Redex: Lightweight Mechanization
We first developed λJS in PLT Redex, a domain-specific language embedded in Racket for specifying operational semantics.
Redex brings dull semantics to life. It doesn't just make a semantics executable, but also lets you visualize it. For example, here is our first example sequence in Redex (parentheses included):
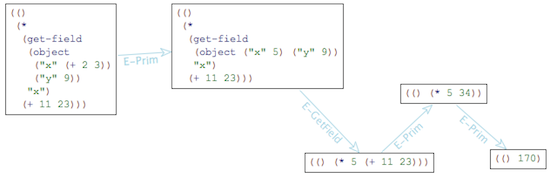
The visualizer is a lot of fun, and a very effective debugging tool. It helped us catch several bugs in the early design of λJS.
Redex can also generate random tests to exercise your semantics. Random testing caught several more bugs in λJS.
Coq: A Machine-Checked Proof
Testing is not enough. We shipped λJS with a bug that breaks the soundness theorem above. We didn't discover it for a year. David van Horn and Ian Zerny both reported it to us independently. We'd missed a case in the semantics, which caused certain terms to get "stuck". It turned out to be a simple fix, but we were left wondering if anything else was left lurking.
To gain further assurance, we mechanized λJS with the Coq proof assistant. The soundness theorem now has a machine-checked proof of correctness. You still need to read the Coq definition of λJS and ensure it matches your intuitions. But once that's done, you can be confident that the proofs are valid.
Doing this proof was surprisingly easy, once we'd read Software Foundations and Certified Programming with Dependent Types. We'd like to thank Benjamin Pierce and his co-authors, and Adam Chlipala, for putting their books online.
What's Done
Here's what we've got so far:
- A PLT Redex model,
- A Coq model, and
- A proof of soundness in Coq.
What's Next
We're not done. Here's what's coming up:
- There are a few easy bits missing from the Coq model (e.g., a parameterized delta-function).
- Once those easy bits are done, we'll wire it together with desugaring.
- Finally, we'll upgrade the model to support semantics for ECMAScript 5.
