Resugaring Type Rules
Tags: Programming Languages, Resugaring, Semantics, Types
Posted on 19 June 2018.This is the final post in a series about resugaring. It focuses on resugaring type rules. See also our posts on resugaring evaluation steps and resugaring scope rules.
No one should have to see the insides of your macros. Yet type errors
often reveal them. For example, here is a very simple and macro in
Rust (of course you should just use && instead, but we’ll use this
as a simple working example):

and the type error message you get if you misuse it:
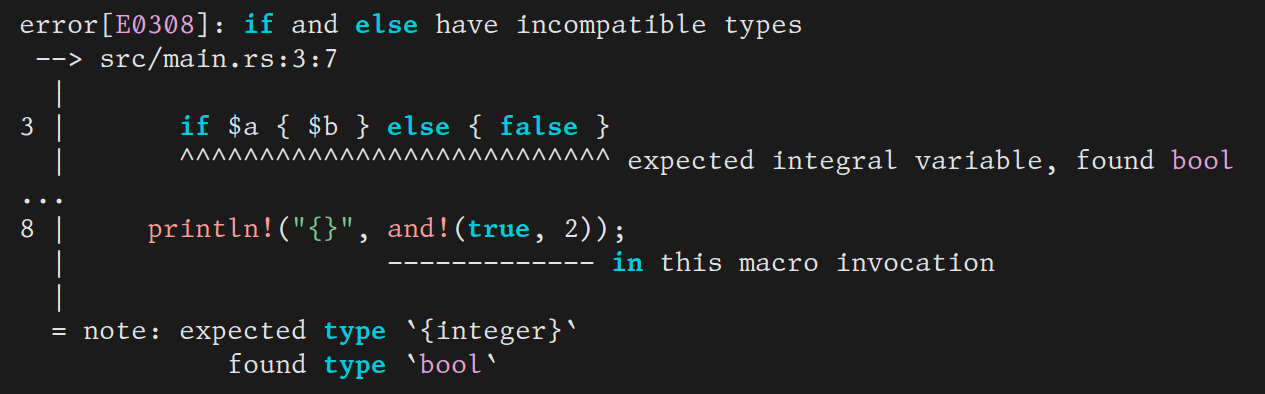
You can see that it shows you the definition of this macro. In this case it’s not so bad, but other macros can get messy, and you might not want to see their guts. Plus in principle, a type error should only show the erronous code, not correct code that it happend to call. You wouldn’t be very happy with a type checker that sometimes threw an error deep in the body of a (type correct) library function that you called, just because you used it the wrong way. Why put up with one that does the same thing for macros?
The reason Rust does is that that it does not know the type of and.
As a result, it can only type check after and has been desugared
(a.k.a., expanded), and so the error occurs in the desugared code.
But what if Rust could automatically infer a type rule for checking
and, using only the its definition? Then the error could be found in
the original program that you wrote (rather than its expansion), and
presented as such. This is exactly what we did—albeit for simpler type
systems than Rust’s—in our recent PLDI’18 paper
Inferring Type Rules for Syntactic Sugar.
We call this process resugaring type rules; akin to our previous work
on
resugaring evaluation steps
and
resugaring scope rules.
Let’s walk through the resugaring of a type rule for and:
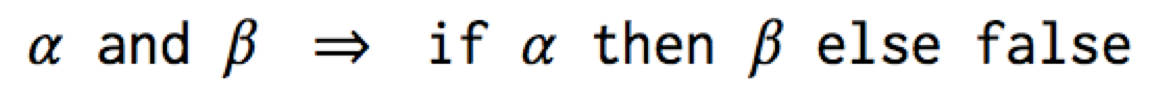
We want to automatically derive a type rule for and, and we want it
to be correct. But what does it mean for it to be correct? Well, the
meaning of and is defined by its desugaring: α and β is synonymous
with if α then β else false. Thus they should have the same type:
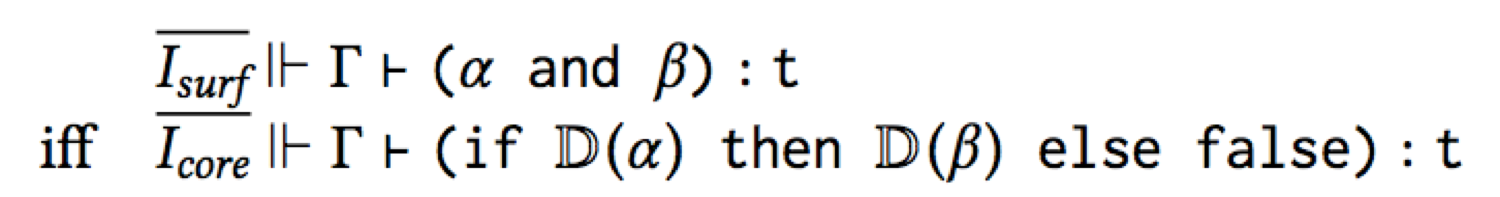
(Isurf ||- means “in the surface language type system”, Icore
||- means “in the core language type system”, and the fancy D means
“desugar”.)
How can we achieve this? The most straightforward to do is to capture
the iff with two type rules, one for the forward implication, and
one for the reverse:
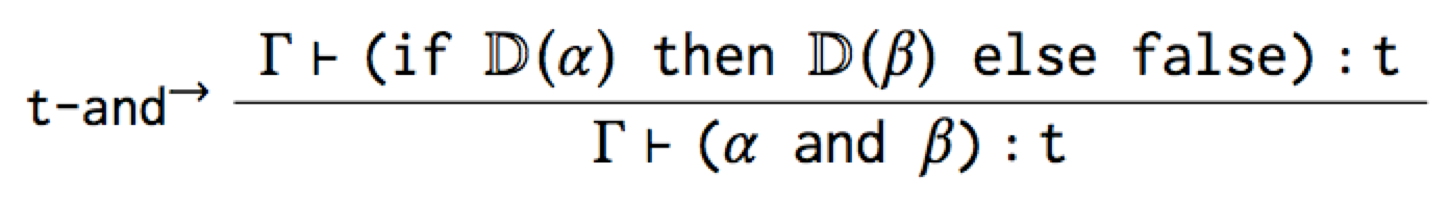
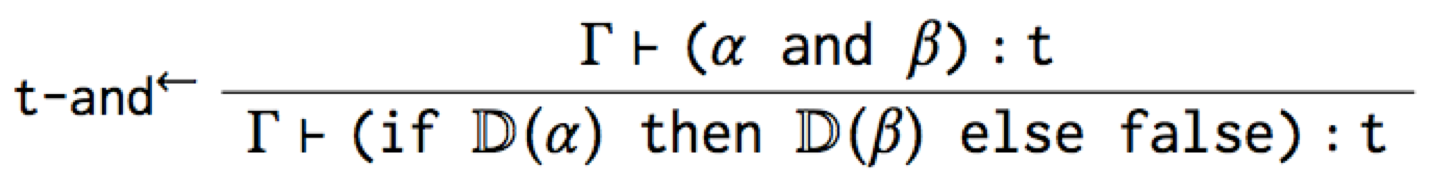
The first type rule is useful because it says how to type check and
in terms of its desugaring. For example, here’s a derivation that
true and false has type Bool:

However, while this t-and→ rule is accurate, it’s not the canonical
type rule for and that you’d expect. And worse, it mentions if, so
it’s leaking the implementation of the macro!
However, we can automatically construct a better type rule. The trick
is to look at a more general derivation. Here’s a generic type
derivation for any term α and β:
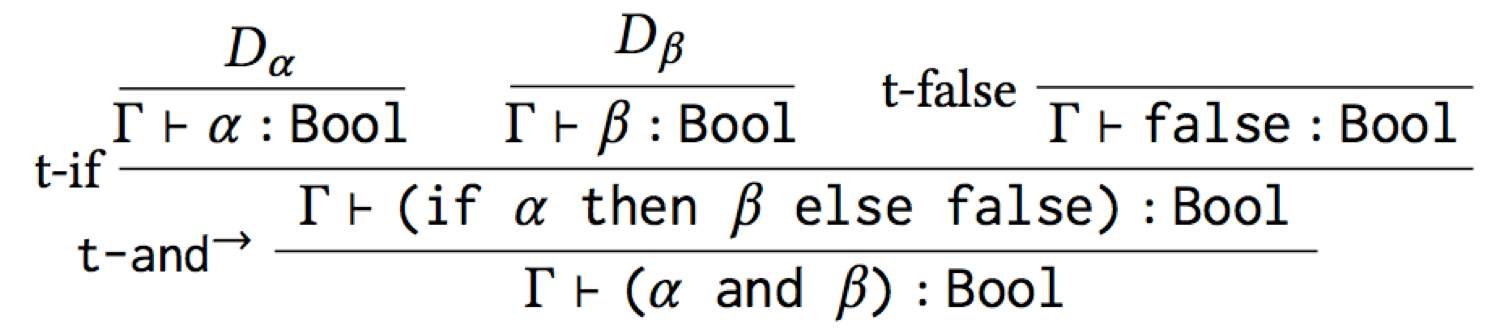
Notice Dα and Dβ: these are holes in the derivation, which ought to be filled in with sub-derivations proving that α has type Bool and β has type Bool. Thus, “α : Bool” and “β : Bool” are assumptions we must make for the type derivation to work. However, if these assumptions hold, then the conclusion of the derivation must hold. We can capture this fact in a type rule, whole premises are these assumptions, and whose conclusion is the conclusion of the whole derivation:
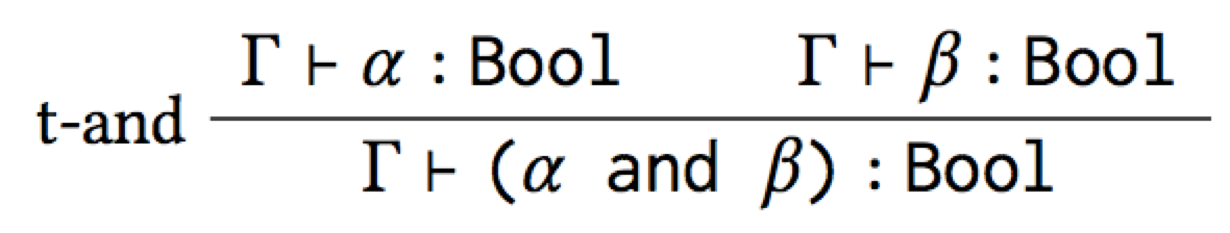
And so we’ve inferred the canonical type rule for and! Notice that
(i) it doesn’t mention if at all, so it’s not leaking the inside of
the macro, and (ii) it’s guaranteed to be correct, so it’s a good
starting point for fixing up a type system to present errors at the
right level of abstraction. This was a simple example for illustrative
purposes, but we’ve tested the approach on a variety of sugars and
type systems.
You can read more in our paper, or play with the implementation.
