Articles by tag: Education
The Pyret Programming Language: Why Pyret?
In-flow Peer Review: An Overview
CS Student Work/Sleep Habits Revealed As Possibly Dangerously Normal
From MOOC Students to Researchers
The New MOOR's Law
Essentials of Garbage Collection
Mystery Languages
Tags: Programming Languages, Education
Posted on 05 July 2018.How do you learn a new language? Do you simply read its reference manual, and then you’re good to go? Or do you also explore the language, trying things out by hand to see how they behave?
This skill—learning about something by poking at it—is frequently used but almost never taught. However, we have tried to teach it via what we dub mystery languages, and this post is about how we went about it.
Mystery Lanuages
A mystery language is exactly what it sounds like: a programming language whose behavior is a mystery. Each assignment comes with some vague documentation, and an editor in which you can write programs. However, when you run a program it will produce multiple answers! This is because there are actually multiple languages, with the same syntax but different semantics. The answers you get are the results of running your program in all of the different languages. The goal of the assignment is to find programs that tell the languages apart.
As an example, maybe the languages have the syntax a[i], and the
documentation says that this “accesses an array a at index i”.
That totally specifies the behavior of this syntax, right?
Not even close. For example, what happens if the index is out of bounds?
Does it raise an error (like Java), or return undefined (like
JavaScript), or produce nonsense (like C), or wrap the index to a
valid one (like Python)? And what happens if the index is 2.5, or
"2", or 2.0, or "two"?
(EDIT: Specifically, Python wraps negative indices that are smaller than the length of the array.)
Students engage with the mystery languages in three ways:
- The first part of each assignment is to find a set of programs that distinguishes the different languages (a.k.a. a classifier).
- The second part of the assignment is to describe a theory that explains the different behaviors of the languages. (For example, a theory about C’s behavior could include accessing heap addresses past the end of an array.)
- Finally, after an assignment is due, there’s an in-class discussion and explanation of the mystery languages. This is especially useful to provide terminology for behaviors that students encountered in the languages.
This example is somewhat superficial (the real mystery languages mostly use more significant features than array access), but you get the idea: every aspect of a programming language comes with many possible designs, and the mystery languages have students explore them first-hand.
Why Mystery Languages?
We hope to teach a number of skills through mystery languages:
- Evaluating Design Decisions: The mystery languages are almost entirely based on designs chosen by real languages: either historical choices that have since been settled, or choices that are still up in the air and vary between modern languages. Students get to explore the consequences of these decisions themselves, so that they get a feel for them. And the next day in class they learn about the broader historical context.
- Syntax vs. Semantics: We are frustrated by how frequently discussions about programming languages revolve around syntax. With luck, showing students first-hand that a single syntax can have a variety of semantics will bring their discussions to a somewhat higher level.
- Adversarial Thinking: Notice that the array example was all about exploring edge cases. If you only ever wrote correct, safe, boring programs then you’d never notice the different ways that array access could work. This is very similar to the kind of thinking you need to do when reasoning about security, and we hope that students might pick up on this mindset.
- Experimental Thinking: In each assignment, students are asked not only to find programs that behave differently across the mystery languages, but also to explain the behavior of the different languages. This is essentially a scientific task: brainstorm hypotheses about how the languages might work; experimentally test these hypotheses by running programs; discard any hypothesis that was falsified; and iterate.
Adopting Mystery Languages
If you want to use Mystery Languages in your course, email us and we’ll help you get started!
There are currently 13 mystery languages, and more in development. At Brown, we structured our programming languages course around these mystery languages: about half of the assignments and half of the lectures were about mystery languages. However, mystery languages are quite flexible, and could also be used as a smaller supplement to an existing course. One possibility is to begin with one or two simpler languages to allow students to learn how they work, and from there mix and match any of the more advanced languages. Alternatively, you could do just one or two mystery languages to meet specific course objectives.
Learn More
You can learn more about mystery languages in our SNAPL’17 paper, or dive in and try them yourself (see the assignments prefixed with “ML:”).
The Pyret Programming Language: Why Pyret?
Tags: Education, Programming Languages, Semantics
Posted on 26 June 2016.We need better languages for introductory computing. A good introductory language makes good compromises between expressiveness and performance, and between simplicity and feature-richness. Pyret is our evolving experiment in this space.
Since we expect our answer to this question will evolve over time, we’ve picked a place for our case for the language to live, and will update it over time:
The Pyret Code; or A Rationale for The Pyret Programming Language
The first version answers a few questions that we expect many people have when considering languages in general and languages for education in particular:
- Why not just use Java, Python, Racket, OCaml, or Haskell?
- Will Pyret ever be a full-fledged programming language?
- But there are lots of kinds of “education”!
- What are some ways the educational philosophy influences the langauge?
In this post, it’s worth answering one more immediate question:
What’s going on right now, and what’s next?
We are currently hard at work on three very important features:
-
Support for static typing. Pyret will have a conventional type system with tagged unions and a type checker, resulting in straightforward type errors without the complications associated with type inference algorithms. We have carefully designed Pyret to always be typeable, but our earlier type systems were not good enough. We’re pretty happy with how this one is going.
-
Tables are a critical type for storing real-world data. Pyret is adding linguistic and library support for working effectively with tables, which PAPL will use to expose students to “database” thinking from early on.
-
Our model for interactive computation is based on the “world” model. We are currently revising and updating it in a few ways that will help it better serve our new educational programs.
On the educational side, Pyret is already used by the Bootstrap project. We are now developing three new curricula for Bootstrap:
-
A CS1 curriculum, corresponding to a standard introduction to computer science, but with several twists based on our pedagogy and materials.
-
A CS Principles curriculum, for the new US College Board Advanced Placement exam.
-
A physics/modeling curriculum, to help teach students physics and modeling through the medium of programming.
If you’d like to stay abreast of our developments or get involved in our discussions, please come on board!
In-flow Peer Review: An Overview
Tags: Education, In-flow Peer Review
Posted on 02 January 2016.We ought to give students opportunities to practice code review. It’s a fundamental part of modern software development, and communicating clearly and precisely about code is a skill that only develops with time. It also helps shape software projects for the better early on, as discussions about design and direction in the beginning can avoid costly mistakes that need to be undone later.
Introducing code review into a curriculum faces a few challenges. First, there is the question of the pedagogy of code review: what code artifacts are students qualified to review? Reviewing entire solutions may be daunting if students are already struggling to complete their own, and it can be difficult to scope feedback for an entire program. Adding review also introduces a time cost for assignments, if it actually makes up a logically separate assignment from the code under review.
We propose in-flow peer review (IFPR) as a strategy for blending some of these constraints and goals. The fundamental idea is to break assignments into separately-submittable chunks, where each intermediate submittable is designed to be amenable to a brief peer review. The goal is for students to practice review, benefit from the feedback they get from their peers while the assignment is still ongoing, and also learn from seeing other approaches to the same problem. We’ve experimented with in-flow peer review in several settings, and future posts will discuss more of our detailed results. Here, we lay out some of the design space of in-flow peer review, including which intermediate steps might show promise, and what other choices a practitioner of IFPR can make. This discussion is based on our experience and on an ITiCSE working group report that explored many of the design dimensions of IFPR. That report has deeper discussions of the topics we introduce here, along with many other design dimensions and examples for IFPR.
What to Submit
The first question we need to address is what pieces of assignments are usefully separable and reviewable. There are a number of factors at work here. For example, it may be detrimental from an evaluation point of view to share too much of a solution while the assignment is ongoing, so the intermediate steps shouldn’t “give away” the whole solution. The intermediate steps need to be small enough to review in a brief time window, but interesting enough to prompt useful feedback. Some examples of intermediate steps are:
- Full test suites for the problem, without the associated solution
- A class or structure definition used to represent a data structure, without the associated operations
- Function headers for helper functions without the associated body
- Full helper functions, without the associated “main” implementation
- A task-level breakdown of a work plan for a project (e.g. interface boundaries, test plan, and class layout)
- A description of properties (expressed as predicates in a programming language, or informally) that ought to be true of an eventual implementation
Each of these reviewable artifacts can give students hints about a piece of the problem without giving away full solutions, and seem capable of prompting meaningful feedback that will inform later stages of the assignment.
How to Review
The second question has to do with the mechanics of review itself. How many submissions should students review (and how many reviews should they receive)? Should students’ names be attached to their submissions and/or their reviews, or should the process be completely anonymous? What prompts should be given in the review rubric to guide students towards giving useful feedback? How much time should students have to complete reviews, and when should they be scheduled in the assignment process?
These questions, obviously, don’t have right or wrong answers, but some in particular are useful to discuss, especially with respect to different goals for different classrooms.
- Anonymity is an interesting choice. Professional code review is seldom anonymous, and having students take ownership of their work encourages an attitude of professionalism. If reviewer-reviewee pairs can identify one another, they can communicate outside the peer review system, as well, which may be encouraged or not desired depending on the course. Anonymity has a number of benefits, in that it avoids any unconscious bias in reviews based on knowing another student’s identity, and may make students feel more comfortable with the process.
- Rubric design can heavily shape the kinds of reviews students write. At one extreme, students could simply get an empty text box and provide only free-form comments. Students could also be asked to identify specific features in their review (“does the test suite cover the case of a list with duplicate elements?”), fill in line-by-line comments about each part of the submission, write test cases to demonstrate bugs that they find, or many other structured types of feedback. This is a pretty wide-open design space, and the complexity and structure of the rubric can depend on curricular goals, and on the expected time students should take for peer review.
- Scheduling reviews and intermediate submissions is an interesting balancing act. For a week-long assignment, it may be useful to have initial artifacts submitted as early as the second day, with reviews submitted on the third day, in order to give students time to integrate the feedback into their submissions. For longer assignments, the schedule can be stretched or involve more steps. This can have ancillary benefits, in that students are forced to start their assignment early in order to participate in the review process (which can be mandatory), combatting procrastination.
Logistics (and Software Support)
Setting up an IFPR workflow manually would involve serious instructor effort, so software support is a must for an easy integration of IFPR into the classroom. The software ought to support different review workflows and rubrics, across various assignment durations in types, in order to be useful in more than one class or setting. In the next post, we’ll talk about some design goals for IFPR software and how we’ve addressed them.
CS Student Work/Sleep Habits Revealed As Possibly Dangerously Normal
Tags: Education, User Studies
Posted on 14 June 2014. Written by Jesse Polhemus, and originally posted at the Brown CS blogImagine a first-year computer science concentrator (let’s call him Luis) e-mailing friends and family back home after a few weeks with Brown Computer Science (BrownCS). Everything he expected to be challenging is even tougher than anticipated: generative recursion, writing specifications instead of implementations, learning how to test his code instead of just writing it. Worst of all is the workload. On any given night, he’s averaging –this seems too cruel to be possible– no more than eight or nine hours of sleep.
Wait, what? Everyone knows that CS students don't get any sleep, so eight or nine hours is out of the question. Or is it? Recent findings from PhD student Joseph Gibbs Politz, adjunct professor Kathi Fisler, and professor Shriram Krishnamurthi analyze when students completed tasks in two different BrownCS classes, shedding interesting light on an age-old question: when do our students work, and when (if ever) do they sleep? The question calls to mind a popular conception of the computer scientist that Luis has likely seen in countless movies and books:
- Hours are late. (A recent poster to boardgames@lists.cs.brown.edu requests a 2 PM start time in order to avoid being “ridiculously early” for prospective players.)
- Sleep is minimal. BrownCS alumnus Andy Hertzfeld, writing about the early days of Apple Computer in Revolution in the Valley, describes the “gigantic bag of chocolate-covered espresso beans” and “medicinal quantities of caffeinated beverages” that allowed days of uninterrupted coding.
Part 1: Deadline Experiments
The story begins a few years before Luis’s arrival, when Shriram would routinely schedule his assignments to be due at the 11:00 AM start of class. “Students looked exhausted,” he remembers. “They were clearly staying up all night in order to complete the assignment just prior to class.”
Initially, he moved the deadline to 2:00 AM, figuring that night owl students would finish work in the early hours of the morning and then get some sleep. This was effective, but someone pointed out that it was unfair to other professors who taught earlier classes and were forced to deal with tired students who had finished Shriram’s assignment but not slept sufficiently.
“My final step,” he explains, “was to change deadlines to midnight. I also began penalizing late assignments on a 24-hour basis instead of an hourly one. This encourages students to get a full night’s sleep even if they miss a deadline.”
This was the situation when Luis arrives. The next task was to start measuring the results.
Part 2: Tracking Events
Shriram, Kathi, and Joe analyzed two of Shriram’s classes, CS 019 and CS 1730. For each class, Luis must submit test suites at any time he chooses, then read reviews of his work from fellow students. He then continues working on the solution, eventually producing a final implementation that must be submitted prior to the midnight deadline.
Part 3: Reality And Mythology
Given these parameters, what work and sleep patterns would you expect? We asked professor Tom Doeppner to reflect on Luis and share his experience of working closely with students as Director of Undergraduate Studies and Director of the Master’s Program. “Do students work late? I know I get e-mail from students at all hours of the night,” he says, “and I found out quickly that morning classes are unpopular, which is why I teach in the afternoon. Maybe it’s associated with age? I liked to work late when I was young, but I got out of the habit in my thirties.”
Asked about the possible mythologizing of late nights and sleeplessness, Tom tells a story from his own teaching: “Before we broke up CS 169 into two classes, the students had t-shirts made: ‘CS 169: Because There Are Only 168 Hours In A Week’. I think there’s definitely a widespread belief that you’re not really working hard unless you’re pulling multiple all-nighters.”
This doesn’t exactly sound like Luis’s sleep habits! Take a look at the graphs below to see how mythology and reality compare.
Part 4: Results And Conclusions
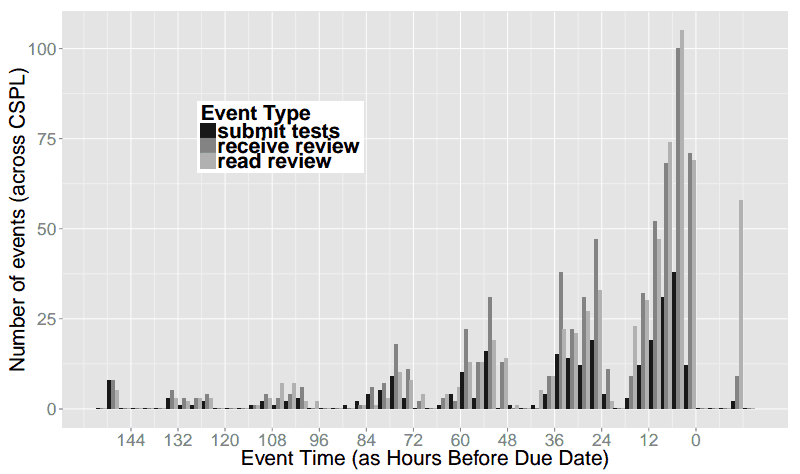
The graphs below depict test suite submissions, with time displayed in six-hour segments. For example, between 6 PM and the midnight deadline (“6-M”), 50 CS 173 students are submitting tests.
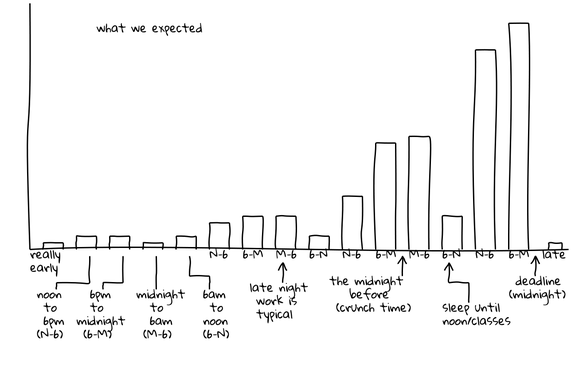
This graph is hypothetical, showing Joe, Kathi, and Shriram’s expectations for submission activity. They expected activity to be slow and increase steadily, culminating in frantic late-night activity just before the deadline. Generally taller “M-6” (midnight to 6 AM) bars indicate late-night work and a corresponding flurry of submissions, followed by generally shorter “6-N” (6 AM to noon) bars when students tried to get a few winks in. Cumulatively, these two trends depict the popular conception of the computer science student who favors late hours and perpetually lacks sleep.
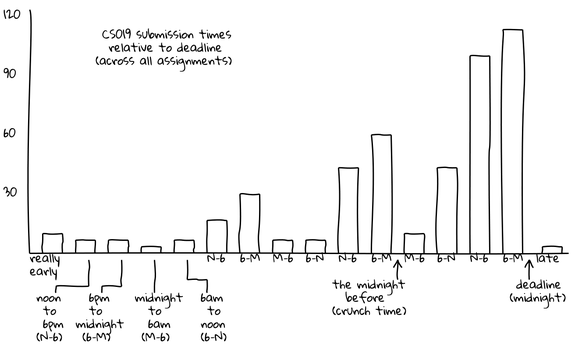
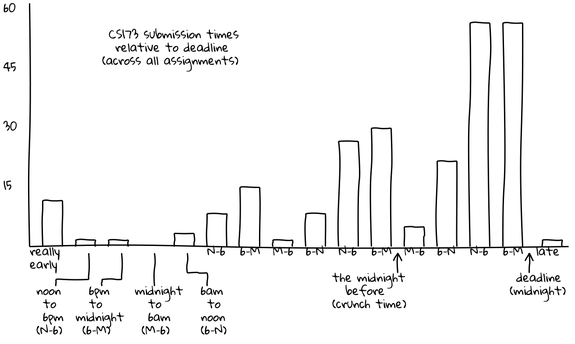
These graphs show actual submissions. As expected, activity generally increases over time and the last day contains the majority of submissions. However, unexpectedly, the “N-6” (noon to 6 PM) and “6-M” (6 PM to midnight) segments are universally the most active. In the case of the CS 173 graph, this morning segment contains far more submissions than any other of the day’s three segments. In both of these graphs, the “M-6” (midnight to 6 AM) segments are universally the least active, even the day the assignment is due. For example, the final segment of this type, which represents the last available span of early morning hours, is among the lowest of all segments, with only ten submissions occurring. In contrast, the corresponding “6-N” (6 AM to noon) shows more than four times as many submissions, suggesting that most students do their work before or after the pre-dawn hours but not during them.
“I wouldn’t have expected that,” Joe comments. “I think of the stories folks tell of when they work not lining up with that, in terms of staying up late and getting up just in time for class. Our students have something important to do at midnight other than work: they cut off their work before midnight and do something else. For the majority it’s probably sleep, but it could just be social time or other coursework. Either way, it’s an interesting across-the-board behavior.”
If word of these results gets out, what can Luis and his fellow students expect? “People will realize,” Shriram says, “that despite what everyone likes to claim, students even in challenging courses really are getting sleep, so it’s okay for them to, too.” Joe agrees: “There isn’t so much work in CS that you have to sacrifice normal sleeping hours for it.”
Luis, his family, and his well-rested classmates will undoubtedly be glad to hear it. The only question is: will their own descriptions of their work/sleep habits change to match reality, or are tales of hyper-caffeinated heroics too tempting to resist?
Appendix
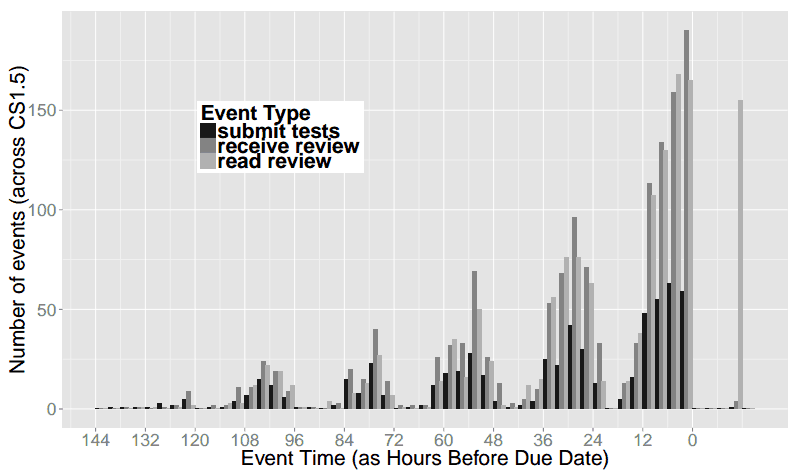
The graphs above are simplified for readability, and aggregated into 6-hour increments. Below we include graphs of the raw data in 3-hour increments. This shows that there is some work going on from 12am-3am the night before assignments are due, but essentially nothing from 3am-6am.
In both of these classes, we were also performing experiments on code review, so the raw data includes when students read the code reviews they received, in addition to when they submitted their work. Since the review necessarily happens after submission, and the reading of the review after that, we see many more “late” events for reading reviews.
CS019 in 3-hour increments:
CS173 in 3-hour increments:
From MOOC Students to Researchers
Tags: Education, Programming Languages, Semantics
Posted on 18 June 2013.Much has been written about MOOCs, including the potential for its users to be treated, in effect, as research subjects: with tens of thousands of users, patterns in their behavior will stand out starkly with statistical significance. Much less has been written about using MOOC participants as researchers themselves. This is the experiment we ran last fall, successfully.
Our goal was to construct a “tested semantics” for Python, a popular programming language. This requires some explanation. A semantics is a formal description of the behavior of a language so that, given any program, a user can precisely predict what the program is going to do. A “tested” semantics is one that is validated by checking it against real implementations of the language itself (such as the ones that run on your computer).
Constructing a tested semantics requires covering all of a large language, carefully translating its every detail into a small core language. Sometimes, a feature can be difficult to translate. Usually, this just requires additional quantities of patience, creativity, or elbow grease; in rare instances, it may require extending the core language. Doing this for a whole real-world language is thus a back-breaking effort.
Our group has had some success building such semantics for multiple languages and systems. In particular, our semantics for JavaScript has come to be used widely. The degree of interest and rapidity of uptake of that work made clear that there was interest in this style of semantics for other languages, too. Python, which is not only popular but also large and complex (much more so than JavaScript), therefore seemed like an obvious next target. However, whereas the first JavaScript effort (for version 3 of the language) took a few months for a PhD student and an undergrad, the second one (focusing primarily on the strict-mode of version 5) took far more effort (a post-doc, two PhD students, and a master's student). JavaScript 5 approaches, but still doesn't match, the complexity of Python. So the degree of resources we would need seemed daunting.
Crowdsourcing such an effort through, say, Mechanical Turk did not seem very feasible (though we encourage someone else to try!). Rather, we needed a trained workforce with some familiarity with the activity of formally defining a programming language. In some sense, Duolingo has a similar problem: to be able to translate documents it needs people who know languages. Duolingo addresses it by...teaching languages! In a similar vein, our MOOC on programming languages was going to serve the same purpose. The MOOC would deliver a large and talented workforce; if we could motivate them, we could then harness them to help perform the research.
During the semester, we therefore gave three assignments to get students warmed up on Python: 1, 2, and 3. By the end of these three assignments, all students in the class had had some experience wrestling with the behavior of a real (and messy) programming language, writing a definitional interpreter for its core, desugaring the language to this core, and testing this desugaring against (excerpts of) real test suites. The set of features was chosen carefully to be both representative and attainable within the time of the course.
(To be clear, we didn't assign these projects only because we were interested in building a Python semantics. We felt there would be genuine value for our students in wrestling with these assignments. In retrospect, however, this was too much work, and it interfered with other pedagogic aspects of the course. As a result, we're planning to shift this workload to a separate, half-course on implementing languages.)
Once the semester was over, we were ready for the real business to begin. Based on the final solutions, we invited several students (out of a much larger population of talent) to participate in taking the project from this toy sub-language to the whole Python language. We eventually ended up with an equal number of people who were Brown students and who were from outside Brown. The three Brown students were undergraduates; the three outsiders were an undergraduate student, a professional programmer, and a retired IT professional who now does triathlons. The three outsiders were from Argentina, China, and India. The project was overseen by a Brown CS PhD student.
Even with this talented workforce, and the prior preparation done through the course and creating the assignments prepared for the course, getting the semantics to a reasonable state was a daunting task. It is clear to us that it would have been impossible to produce an equivalent quality artifact—or to even come close—without this many people participating. As such, we feel our strategy of using the MOOC was vindicated. The resulting paper has just been accepted at a prestigious venue that was the most appropriate one for this kind of work, with eight authors: the lead PhD student, the three Brown undergrads, the three non-Brown people, and the professor.
A natural question is whether making the team even larger would have helped. As we know from Fred Brooks's classic The Mythical Man Month, adding people to projects can often hurt rather than help. Therefore, the determinant is to what extent the work can be truly parallelized. Creating a tested semantics, as we did, has a fair bit of parallelism, but we may have been reaching its limits. Other tasks that have previously been crowdsourced—such as looking for stellar phenomena or trying to fold proteins—are, as the colloquial phrase has it, “embarrassingly parallel”. Most real research problems are unlikely to have this property.
In short, the participants of a MOOC don't only need to be thought of as passive students. With the right training and motivation, they can become equal members of a distributed research group, one that might even have staying power over time. Also, participation in such a project can help a person establish their research abilities even when they are at some remove from a research center. Indeed, the foreign undergraduate in our project will be coming to Brown as a master's student in the fall!
Would we do it again? For this fall, we discussed repeating the experiment, and indeed considered ways of restructuring the course to better support this goal. But before we do, we have decided to try to use machine learning instead. Once again, machines may put people out of work.
The New MOOR's Law
Posted on 01 April 2013.
Though this was posted on April 1, and the quotes in this article should be interpreted relative to that date, MOOR itself is not a joke. Students from our online course produced a semantics for Python, with a paper describing it published at OOPSLA 2013.
PROVIDENCE, RI, USA - With the advent of Massively Open and Online Courses (MOOCs), higher education faces a number of challenges. Services like Udacity and Coursera will provide learning services of equivalent quality for a fraction of the cost, and may render the need for traditional education institutions obsolete. With the majority of universities receiving much of their cash from undergraduate tuition, this makes the future of academic research uncertain as well.
"[Brown]
lacks the endowment of a school like Harvard to weather the coming
storm."
-Roberto Tamassia
Schools may eventually adapt, but it's unclear what will happen to research programs in the interim. “I'm concerned for the future of my department at Brown University, which lacks the endowment of a school like Harvard to weather the coming storm,” said Roberto Tamassia, chair of the Computer Science department at Brown.
But one Brown professor believes he has a solution for keeping his research program alive through the impending collapse of higher education. He calls it MOOR: Massively Open and Online Research. The professor, Shriram Krishnamurthi, claims that MOOR can be researchers' answer to MOOCs: “We've seen great user studies come out of crowdsourcing platforms like Mechanical Turk. MOOR will do the same for more technical research results; it's an effective complement to Turk.”
"MOOR ...
is an effective complement to [Mechanical] Turk."
-Shriram Krishnamurthi
MOOR will reportedly leverage the contributions of novice scholars from around the globe in an integrated platform that aggregates experimental results and proposed hypotheses. This is combined with a unique algorithm that detects and flags particularly insightful contributions. This will allow research results never before possible, says Joe Gibbs Politz: “I figure only one in 10,000 people can figure out decidable and complete principal type inference for a language with prototype-based inheritance and equirecursive subtyping. So how could we even hope to solve this problem without 10,000 people working on it?”
Krishnamurthi has historically recruited undergraduate Brown students to aid him in his research efforts. Leo Meyerovich, a former Krishnamurthi acolyte, is excited about changing the structure of the educational system, and shares concerns about Krishnamurthi's research program. With the number of undergraduates sure to dwindle to nothing in the coming years, he says, “Shriram will need to come up with some new tricks.”
Brown graduates Ed Lazowska and Peter Norvig appear to agree. While Lazowska refused to comment on behalf of the CRA, saying its position on the matter is “still evolving,” speaking personally, he added, “evolve or die.” As of this writing, Peter Norvig has pledged a set of server farms and the 20% time of 160,000 Google Engineers to support MOOR.
With additional reporting from Kathi Fisler, Hannah Quay-de la Vallee, Benjamin S. Lerner, and Justin Pombrio.
Essentials of Garbage Collection
Tags: Education
Posted on 19 February 2013.How do we teach students the essential ideas behind garbage collection?
A garbage collector (GC) implementation must address many overlapping concerns. There are algorithmic decisions, e.g., the GC algorithm to use; there are representation choices, e.g, the layout of the stack; and there are assumptions about the language, e.g., unforgeable pointers. These choices, and more, affect each other and make it very difficult for students to get off the ground.
Programming language implementations can be similarly complex. However, over the years, starting from McCarthy's seminal paper, we've found it invaluable to write definitional interpreters for simple core languages, that allow us to easily explore the consequences of language design. What is the equivalent for garbage collectors?
Testing and Curricular Dependencies
Testing is important for any program, and is doubly so for a garbage collector, which must correctly deal with complex inputs (i.e., programs!). Furthermore, correctness itself is subtle: besides being efficient, a collector must terminate, be sound (not collect non-garbage), be effective (actually collect enough true garbage), and preserve the essential structure of live data: e.g., given a cyclic datum, it must terminate, and given data with sharing, it must preserve the sharing-structure and not duplicate data.
For instructors, a further concern is the number of deep, curricular dependencies that teaching GC normally incurs. In a course where students already learn compilers and interpreters, it is possible (but hard) to teach GC. However, GC should be teachable in several contexts, such as a systems course, an architecture course, or even as a cool application of graph algorithms. Eliminating GC's curricular dependencies is thus valuable.
Even in courses that have student implement compilers or interpreters, testing a garbage collector is very hard. A test-case is a program that exercises the collector in an interesting way. Good tests require complex programs, and complex programs require a rich programming language. In courses, students tend to write compilers and interpreters for simple, core languages and are thus stuck writing correspondingly simple programs. Worse, some important GC features, such as the treatment of cycles and first-class functions, are impossible to test unless the programming language being implemented has the necessary features. Growing a core language for the sake of testing GC would be a case of the tail wagging the dog.
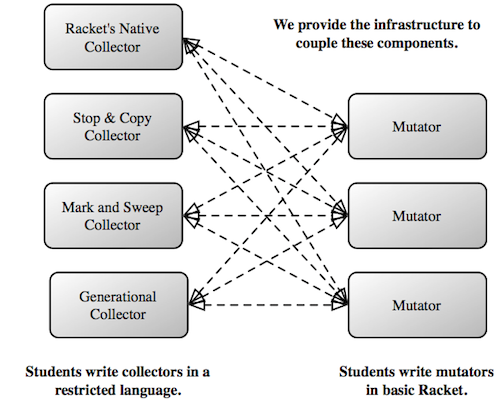
In short, we would like a pedagogic framework where:
- Students can test their collectors using a full-blown programming language, instead of a stilted core language, and
- Students can experiment with different GC algorithms and data-representations, without learning to implement languages.
The Key Idea
Over the past few years, we've built a framework for teaching garbage collection, first started by former Brown PhD student Greg Cooper.
Consider the following Racket program, which would make a great test-case for a garbage collector (with a suitably small heap):
#lang racket
(define (map f l)
(cond
[(empty? l) empty]
[(cons? l) (cons (f (first l))
(map f (rest l)))]))
(map (lambda (x) (+ x 1)) (list 1 2 3))
As written, Racket's native garbage collector allocates the closure
created by lambda and the lists created by cons
and list. But, what if we could route these calls to a
student-written collector and have it manage memory instead?
Greg made the following simple observation. Why are these values being managed by the Racket memory system? That's because the bindings for lambda, cons and list (and other procedures and values) are provided by #lang racket. Instead, suppose that with just one change, we could swap in a student-written collector:
#lang plai/mutator (allocator-setup "my-mark-and-sweep.rkt" 30)Using the magic of Racket's modules and macros, #lang plai/mutator maps memory-allocating procedures to student-written functions. The student designates a module, such as my-mark-and-sweep that exports a small, prescribed interface for memory allocation. That module allocates values in a private heap and runs its own GC algorithm when it runs out of space. In our framework, the heap size is a parameter that is trivial to change. The program above selects a heap size of 30, which is small enough to trigger several GC cycles.
We've designed the framework so that students can easily swap in different collectors, change the size of the heap, and even use Racket's native collector, as a sanity check.
Discovering GC Roots
Routing primitive procedures and constants is only half the story. A collector also needs to inspect and modify the program stack, which holds the roots of garbage collection. Since we allow students to write programs in Racket, the stack is just the Racket stack, which is not open for reflection. Therefore, we must also transform the program to expose the contents of the stack.
Our framework automatically transforms Racket programs to A-normal form, which names all intermediate expressions in each activation record. Unlike other transformations, say CPS, A-normalization preserves stack-layout. This makes it easy for students to co-debug their programs and collectors using the built-in DrRacket debugger.
In addition to inspecting individual activation records, a collector also needs to traverse the entire list of records on the stack. We maintain this list on the stack itself using Racket's continuation marks. Notably, continuation marks preserve tail-calls, so the semantics of Racket programs are unchanged.
The combination of A-normalization and continuation marks gives us a key technical advantage. In their absence, we would have to manually convert programs to continuation-passing style (followed by defunctionalization) to obtain roots. Not only would these be onerous curricular dependencies, but they would make debugging very hard.
Controlling and Visualizing the Heap
Of course, we would like to prevent collectors from cheating. An easy way to cheat is to simply allocate on the Racket heap. We do not go to great lengths to prevent all forms of cheating (these are carefully-graded homeworks, after all). However, we do demand that collectors access the “heap” through a low-level interface (where the heap is actually just one large Racket array). This interface prevents the storage of non-flat values, thereby forcing students to construct compound representations for compound data. Notably, our framework is flexible enough that we have students design their own memory representations.
The low-level heap interface has an added benefit. Because our
framework can tell “where the heap is”, and has access to the
student's heap-inspection procedures, we are able to provide a
fairly effective heap visualizer:

Learn More
We've been using this framework to teach garbage collection for several years at several universities. It is now included with Racket, too. If you'd like to play with the framework, check out one of our GC homework assignments.
A pedagogic paper about this work will appear at SIGCSE 2013.
References
[1] John Clements and Matthias Felleisen. A Tail-Recursive Machine with Stack Inspection. ACM Transactions on Programming Languages and Systems (TOPLAS), Vol. 26, No. 6, November 2004. (PDF)
[2] Gregory H. Cooper, Arjun Guha, Shriram Krishnamurthi, Jay McCarthy, and Robert Bruce Findler. Teaching Garbage Collection without Implementing Compilers or Interpreters. In ACM Technical Symnposium on Computer Science Education (SIGCSE) 2013. (paper)
[3] Cormac Flanagan, Amr Sabry, Bruce F. Duba, and Matthias Felleisen. The Essence of Compiling with Continuations. In ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), 1993. (PDF)
[4] John McCarthy. Recursive Functions of Symbolic Expressions and their Computation by Machine, Part 1. Communications of the ACM, Volume 3, Issue 4, April 1960. (paper)
