Picking Colors for Pyret Error Messages
Tags: Pyret, Visualization
Posted on 11 June 2018.Pyret has beautiful error messages, like this one:
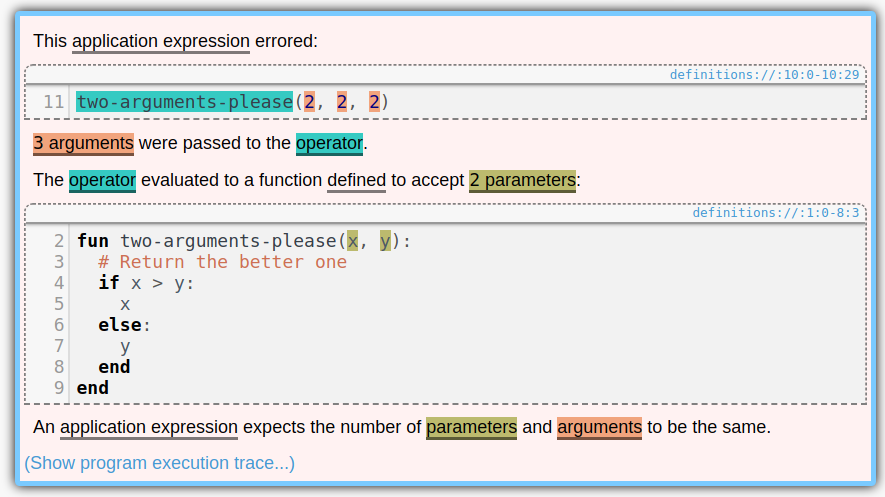
Notice the colors. Aren’t they pretty? Whenever a section of code is mentioned in an error message, it gets highlighted with its own color. And we pick colors that are as different as possible, so they don’t get confused with each other. It is useful to keep all of the colors distinct because it provides a very intuitive one-to-one mapping between parts of the code you wrote and the code snippets mentioned in the error messages. If two error messages used the same color for a snippet, it might look at first glance that they were mentioning the same thing.
(We should say up front: while we believe that the approach described in this post should be fairly robust to most forms of color blindness, it’s difficult to reason about so we make no guarantees. However, if two colors are hard to distinguish by sight, you can always hover over one of them to see the matching section of code blink. EDIT: Actually, it’s not as robust as we had hoped. If you know a good approach to this, let us know.)
How did we make them? It should be easy, right? We could have a list of, say, six colors and use those. After all, no error message needs more than six colors.
Except that there might be multiple error messages. In fact, if you have failing test cases, then you’ll have one failure message per failing test case, each with its own highlight, so there is no upper bound on how many colors we need. (Pyret will only show one of these highlights at a time—whichever one you have selected—but even so it’s nice for them to all have different colors.) Thus we’ll need to be able to generate a set of colors on demand.
Ok, so for any given run of the program, we’ll first determine how many colors we need for that run, and then generate that many colors.
Except that it’s difficult to tell how many colors we need beforehand. In fact, Pyret has a REPL, where users can evaluate expressions, which might throw more errors. Thus it’s impossible to know how many colors we’ll need beforehand, because the user can always produce more errors in the REPL.
Therefore, however we pick colors, it must satisfy these two properties:
- Distinctness: all of the colors in all of the highlights should be as visually different from each other as possible.
- Streaming: we must always be able to pick new colors.
Also, the appearance of the highlights should be pretty uniform; none of them should stand out too much:
- Uniformity: all of the colors should have the same saturation (i.e. colorfulness) and lightness as each other. This way none of them blend in with the background color (which is white) or the text color (which is black), or stand out too much.
The Phillotactic Color-Picking Algorithm
Now let’s talk about the algorithm we use!
(Note that this is “phillotactic”, not “phyllotactic”. It has nothing to do with plants.)
To keep uniformity, it makes sense to pick colors from a rainbow. This is a circle in color space, with constant saturation and lightness and varying hue. Which color space should we use? We should not use RGB, because that space doesn’t agree well with how colors actually appear. For example, if we used a rainbow in RGB space, then green would appear far too bright and blue would appear far too dark. Instead, we should use a color space that agrees with how people actually perceieve colors. The CIELAB color space is better. It was designed so that if you take the distance between two colors in it, that distance approximately agrees with how different the colors seem when you look at them. (It’s only approximate because—among other things—perceptual color space is non-Euclidean.)
Therefore we’ll pick colors from a circle in CIELAB space. This space
has three coordinates: L, for lightness, A for green-red, and B for
blue-yellow (hence the LAB). We determined by experimentation that a
good lightness to use was 73 out of 100. Given this lightness, we
picked the largest saturation possible, using A^2 + B^2 = 40^2.
Now how do we vary the hue? Every color picked needs a new hue, and they need to all be as different as possible. It would be bad, for instance, if we picked 13 colors, and then the 13th color looked just like the 2nd color.
Our solution was to have each color’s hue be the golden angle from the previous hue. From Wikipedia, the golden angle is “the angle subtended by the smaller arc when two arcs that make up a circle are in the golden ratio”. It is also 1/ϕ^2 of a circle, or about 137 degrees.
Thus the phillogenic algorithm keeps track of the number of colors generated so far, and assigns the n’th color a hue of n times the golden angle. So the first color will have a hue of 0 degrees. The second color will have a hue of 137 degrees. The third will have a hue of 137 * 2 = 274 degrees. The fourth will be 137 * 3 = 411 = 51 degrees. This is a little close to the first color. But even if we knew we’d have four colors total, they’d be at most 90 degrees apart, so 51 isn’t too bad. This trend continues: as we pick more and more colors, they never end up much closer to one another than is necessary.
There’s a reason that no two colors end up too similar. It follows from the fact that ϕ is the most difficult number to approximate as a fraction. Here’s a proof that colors aren’t similar:
Suppose that the m’th color and the (m+n)’th color end up being very similar. The difference between the m’th and (m+n)’th colors is the same as the difference between the 0’th and the n’th colors. Thus we are supposing that the 0’th color and the n’th color are very similar.
Let’s measure angles in turns, or fractions of 360 degrees. The n’th
color’s hue is, by definition, n/ϕ^2 % 1 turns. The 0’th hue is 0.
So if these colors are similar, then n/ϕ^2 % 1 ~= 0 (using ~=
for “approximately equals”). We can then reason as follows, using in
the third step the fact that ϕ^2 - ϕ - 1 = 0 so ϕ^2 = ϕ + 1:
n/ϕ^2 % 1 ~= 0
n/ϕ^2 ~= k for some integer k
ϕ^2 ~= n/k
1 + ϕ ~= n/k
ϕ ~= (n-k)/k
Now, if n is small, then k is small (because n/k ~= ϕ^2), so
(n-k)/k is a fraction with a small denominator. But ϕ is difficult
to approximate with fractions, and the smaller the denominator the
worse the approximation, so ϕ actually isn’t very close to
(n-k)/k, so n/ϕ^2 % 1 actually isn’t very close to 0, so the
n’th color actually isn’t very similar to the 0’th color.
And that’s why the phillotactic colors work.
