Articles by tag: Types

Argus: Interactively Debugging Rust trait Errors
Privacy-Respecting Type Error Telemetry at Scale
A Grounded Conceptual Model for Ownership Types in Rust
Typed-Untyped Interactions: A Comparative Analysis
Gradual Soundness: Lessons from Static Python
A Benchmark for Tabular Types
Resugaring Type Rules
The Pyret Programming Language: Why Pyret?
Typechecking Uses of the jQuery Language
Verifying Extensions' Compliance with Firefox's Private Browsing Mode
(Sub)Typing First Class Field Names
Typing First Class Field Names
Progressive Types
ADsafety

Argus: Interactively Debugging Rust trait Errors

Tags: Rust, Tools, Types, User Studies

Posted on 29 April 2025.

Traits are a source of bewildering error messages in the Rust community and people have spent money and time trying to improve the resulting diagnostics. We took a different approach. We analyzed a community suite of difficult-to-debug trait errors and formed hypotheses about why they were difficult for engineers to debug. Then, we built an interactive debugger that developers can use in the IDE to debug trait errors. Find more details about our process, the tool, and our paper in our Cognitive Engineering Lab blog post.

Privacy-Respecting Type Error Telemetry at Scale

Tags: Privacy, Types, User Studies

Posted on 02 February 2024.

Thesis: Programming languages would benefit hugely from telemetry. It would be extremely useful to know what people write, how they edit, what problems they encounter, etc. Problem: Observing programmers is very problematic. For students, it may cause anxiety and thereby hurt their learning (and grades). For professionals too it may cause anxiety, but it can also leak trade secrets.

One very partial solution is to perform these observations in controlled settings, such as a lab study. The downside is that it is hard to get diverse populations of users, it’s hard to retain them for very long, it’s hard to pay for these studies, etc. Furthermore, the activities they perform in a lab study may be very different from what they would do in real use: i.e., lab studies especially lack ecological validity when compared against many real-world programming settings.

We decided to instead study a large number of programmers doing their normal work—but in a privacy-respecting way. We collaborated with the Roblox Studio team on this project. Roblox is a widely-used platform for programming and deploying games, and it has lots of users of all kinds of ages and qualifications. They range from people writing their first programs to developers working for game studios building professional games.

In particular, we wanted to study a specific phenomenon: the uptake of types in Luau. Luau is an extension of Lua that powers Roblox. It supports classic Lua programs, but also lets programmers gradually add types to detect bugs at compile time. We specifically wanted to see what kind of type errors people make when using Luau, with the goal of improving their experience and thereby hopefully increasing uptake of the language.

Privacy-respecting telemetry sounds wonderful in theory but is very thorny in practice. We want our telemetry to have several properties:

It must not transmit any private information. This may be more subtle than it sounds. Error messages can, for instance, contain the names of functions. But these names may contain a trade secret.
It must be fast on the client-side so that the programmer experience is not disrupted.
It must transmit only small amount of data, so as not to overload the database servers.

(The latter two are not specific to privacy, but are necessary when working at scale.)

Our earlier, pioneering work on error message analysis was able to obtain a large amount of insight from logs. As a result of the above constraints, we cannot even pose many of the same questions in our setting.

Nevertheless, we were able to still learn several useful things about Luau. For more details, see the paper. But to us, this project is at least as interesting for the questions it inspires as for the particular solution or the insights gained from it. We hope to see many more languages incorporate privacy-respecting telemetry. (We’re pleased to see the Go team also thinking about these issues, as summarized in Russ Cox’s transparent telemetry notes. While there are some differences between our approaches, our overarching goals and constraints are very much in harmony.)

A Grounded Conceptual Model for Ownership Types in Rust

Tags: Crowdsourcing, Education, Rust, Types, User Studies, Visualization

Posted on 17 September 2023.

Rust is establishing itself as the safe alternative to C and C++, making it an essential component for building a future software univers that is correct, reliable, and secure. Rust achieves this in part through the use of a sophisticated type system based on the concept of ownership. Unfortunately, ownership is unfamiliar to most conventionally-trained programmers. Surveys suggest that this central concept is also one of Rust’s most difficult, making it a chokepoint in software progress.

We have spent over a year understanding how ownership is currently taught, in what ways this proves insufficient for programmers, and looked for ways to improve their understanding. When confronted with a program containing an ownership violation, we found that Rust learners could generally predict the surface reason given by the compiler for rejecting the program. However, learners could often could not relate the surface reason to the underlying issues of memory safety and undefined behavior. This lack of understanding caused learners to struggle to idiomatically fix ownership errors.

To address this, we created a new conceptual model for Rust ownership, grounded in these studies. We then translated this model into two new visualizations: one to explain how the type-system works, the other to illustrate the impact on run-time behavior. Crucially, we configure the compiler to ignore borrow-checker errors. Through this, we are able to essentially run counterfactuals, and thereby illustrate the ensuing undefined behavior.

Here is an example of the type-system visualization:

A visualization of how the borrow checker works on a safe Rust program, using the metaphor of permissions to explain permissible operations at each step.

And here is an example of the run-time visualization:

A visualization of the state of memory at each stateent of an unsafe Rust program, showing how undefined behavior occurs with a use-after-free.

We incorporated these diagrams into an experimental version of The Rust Programming Language by Klabnik and Nichols. The authors graciously permitted us to create this fork and publicize it, and also provided a link to it from the official edition. As a result, we were able to test our tools on readers, and demonstrate that they do actually improve Rust learning.

The full details are in the paper. Our view is that the new tools are preliminary, and other researchers may come up with much better, more creative, and more effective versions of them. Rather, the main contribution is an understanding of how programmers do and don’t understand ownership, and in particular its relationship to undefined behavior. It is therefore possible that new pedagogies that make that connection clear may obviate the need for some of these tools entirely.

Typed-Untyped Interactions: A Comparative Analysis

Tag: Types

Posted on 06 February 2023.

Dozens of languages today support gradual typing in some form or another. What lessons can the designer of a new language learn from their experiences?

As a starting point, let’s say that we want to maximize interoperability. For most types in the language, untyped code should be able to make a value that works for that type: type Number should accept untyped numbers, type List(Number) should accept untyped lists, and so on.

(This may seem like an obvious requirement for a type system that gets added on top of an untyped language. But there are good reasons to break it — see our earlier post on Static Python.)

The question now becomes: what sort of validation strategy should typed code use when an untyped value tries to cross a type boundary? For example, when a Number -> Number type receives an untyped function there are at least three viable options:

Wrap the function in a proxy to make sure its behavior matches the type.
Leave the function unwrapped, but put checks at its call sites.
Do nothing! Trust the function.

Both the research literature and the realm of production-ready languages are full of ideas on this front. What was unclear (until now!) is how the validation strategies implicit across the landscape relate to one another.

With this paper, we introduce a toolbox of formal properties to pin down the guarantees that gradual types can provide:

type soundness (generalized) for local type guarantees,
complete monitoring for compositional type guarantees,
blame soundness to judge the accuracy of validation errors, and
blame completeness to judge the precision of validation errors.

We also use an error preorder to rank strategies by how early they can detect a type validation mismatch.

The upshot of all this is a positive characterization of the landscape. There is no clear winner because there are other factors at play, such as performance costs and the usefulness of types for debugging. What we do gain is a solid theoretical foundation to inform language designs.

It’s all in the paper.

Gradual Soundness: Lessons from Static Python

Tags: Python, Types, User Studies

Posted on 28 June 2022.

It is now virtually a truism that every dynamic language adopts a gradual static type system. However, the space of gradual typing is vast, with numerous tradeoffs between expressiveness, efficiency, interoperability, migration effort, and more.

This work focuses on the Static Python language built by the Instagram team at Meta. Static Python is an interesting language in this space for several reasons:

It is designed to be sound.
It is meant to run fast.
It is reasonably expressive.

The static type system is a combination of what the literature calls concrete and transient types. Concrete types provide full soundness and low performance overhead, but impose nonlocal constraints. Transient types are sound in a shallow sense and easier to use; they help to bridge the gap between untyped code and typed concrete code. The net result is a language that is in active use, with high performance, inside Meta.

Our work here is to both formalize and assess the language. We investigate the language’s soundness claims and report on its performance on both micro-benchmarks and in production systems. In particular, we find that the design holds up the intent of soundness well, but the act of modeling it uncovered several bugs (including one that produced a segmentation fault), all of which have now been fixed.

We believe Static Python is a particularly interesting language for the gradual typing community to study. It is not based on virtuoso theoretical advances; rather, it takes solid ideas (e.g., from Muehlboeck and Tate’s Nom language), combines them well, and pays attention to the various affordances needed by practicing programmers. It therefore offers useful advice to the designers of other gradually-typed languages, in particular those who confront large code-bases and would like incremental approaches to transition from dynamic safety to static soundness. You can read much more about this in the paper.

As an aside, this paper is a collaboration that was born entirely thanks to Twitter and most probably would never have occurred withtout it. An aggrieved-sounding post by Guido van Rossum led to an exchange between Carl Meyer at Meta and Shriram, which continued some time later here. Eventually they moved to Direct Messaging. Shriram pointed out that Ben Greenman could investigate this further, and from that, this collaboration was born.

A Benchmark for Tabular Types

Tags: Programming Languages, Pyret, Semantics, Tables, Types

Posted on 21 November 2021.

Tables are Everywhere

Tables are ubiquitous in the world. Newspapers print tables. Reports include tables. Even children as young as middle-school work comfortably with tables. Tables are, of course, also ubiquitous in programming. Because they provide an easy-to-understand, ubiquitous, already-parsed format, they are also valuable in programming education (e.g., DCIC works extensively with tables before moving on to other compound datatypes).

(Typed) Programming with Tables

When it comes to programming with tables, we have excellent tools like relational databases. However, using external databases creates impedance mismatches, so many programmers like to access tabular data from directly in the language, rather than construct external calls. The popularity of language-embedded query has not diminished with time.

Programming with tables, however, requires attention to types. Tables are inherently heterogeneous: each column is welcome to use whatever type makes most sense. This is all the more so if tables are a part of the language itself: while external data tend to be limited to “wire-format” types like numbers and strings, inside the language they can contain images, functions, other tables, and more. (For instance, we use all of these in Pyret.)

What is the type of a table? To make the output of tabular operations useful, it can’t be something flat like just Table. Because tables are heterogenous, they can’t have just a single type parameter (like Table<T>). It may conceptually make sense to have a type parameter for each column (e.g., Table<String, Number>), but real-world tables can have 17 or 37 columns! Programmers also like to access table columns by name, not only position. And so on.

Making Results Comparable

In Spring 2021, we ran a seminar to understand the state of knowledge of type systems for tables. While we read several excellent papers, we also came away very frustrated: authors simply did not seem to agree on what a “table” was or what operations to support. The result was an enormous degree of incommensurability.

Therefore, rather than invent Yet Another Tabular Type System, we decided to take a step back and address the incommensurability problem. What we need as a community is a shared, baseline understanding of several aspects of tables. That is what this work does: create a tables benchmark. This is not a performance benchmark, however; rather, it’s an expressivity and design benchmark. We call it B2T2: The Brown Benchmark for Tabular Types.

The benchmark doesn’t spring out of thin air. Rather, we extensively studied tabular support in widely-used industrial languages/libraries: R, Python/Pandas, and Julia. To cover educational needs, we also studied the Pyret-based Bootstrap:Data Science curriculum. You will notice that all are based on dynamic languages. (Though Pyret has an optional static type system, it currently does not support tables in any meaningful manner, so tabular programming is essentially dynamic.) This is intentional! If you start with a typed language, you end up reflecting the (potentially artificial and overly-restrictive) constraints of that type system. Rather, it’s healthy to study what programmers (seem to) want to say and do, filter these for reasonability, and reconcile that with the needs of static types (like decidability).

Do Now!

What do you expect to find in a tabular programming benchmark?

Make a list before you read on!

Benchmark Components

B2T2 has the following parts:

A definition of a table. There is actually a large space of possibilities here. We’ve chosen a definition that is both broad and interesting without being onerous.
Examples of tables. Why did we bother to provide these? We do so because many type systems may have all sorts of internal encodings. They are welcome to do so, but they cannot expect the outside world to conform to their representation. Therefore, these examples represent the canonical versions of these tables. Explaining how these will be converted to the internal format is the responsibility of the type system designers.
An API of table operations. This is of course the heart of the benchmark. In particular, different papers seem to use different subsets of operations. What is unclear is whether the missing operations are just as easy as the ones shown; difficult; or even impossible. This is therefore a big source of incommensurability.
Example programs. Depending on the representation of tables and the nature of the type systems and languages, these programs may have to be rewritten and may (to some observers) look quite unnatural.

All these might be predictable with some thought. There are two more components that may be a little more surprising:

Erroneous programs. In all sophisticated systems, there is a trade-off between complexity and explainability. We are disturbed by how little discussion there is of error-reporting in the papers we’ve read, and think the community should re-balance its emphasis. Even those who only care about technical depth (boo!) can take solace: there can be rich technical work in explaining errors, too! Furthermore, by making errors an explicit component, a team that does research into human factors—even if they leave all other aspects alone—has a “place to stand” to demonstrate their contribution.
A datasheet. To improve commensurability, we want authors to tell each other—and their users—in a standard format not only what they did but also where the bodies are buried.

Of course, all these parts are interesting even in the absence of types. We just expect that types will impose the most interesting challenges.

An Open Process

We expect this benchmark to grow and evolve. Therefore, we’ve put our benchmark in a public repository. You’re welcome to make contributions: correct mistakes, refine definitions, add features, provide more interesting examples, etc. You can also contribute solutions in your favorite language!

For More Details

You can read about all this in our paper and work with our repository.

Resugaring Type Rules

Tags: Programming Languages, Resugaring, Semantics, Types

Posted on 19 June 2018.

This is the final post in a series about resugaring. It focuses on resugaring type rules. See also our posts on resugaring evaluation steps and resugaring scope rules.

No one should have to see the insides of your macros. Yet type errors often reveal them. For example, here is a very simple and macro in Rust (of course you should just use && instead, but we’ll use this as a simple working example):

and the type error message you get if you misuse it:

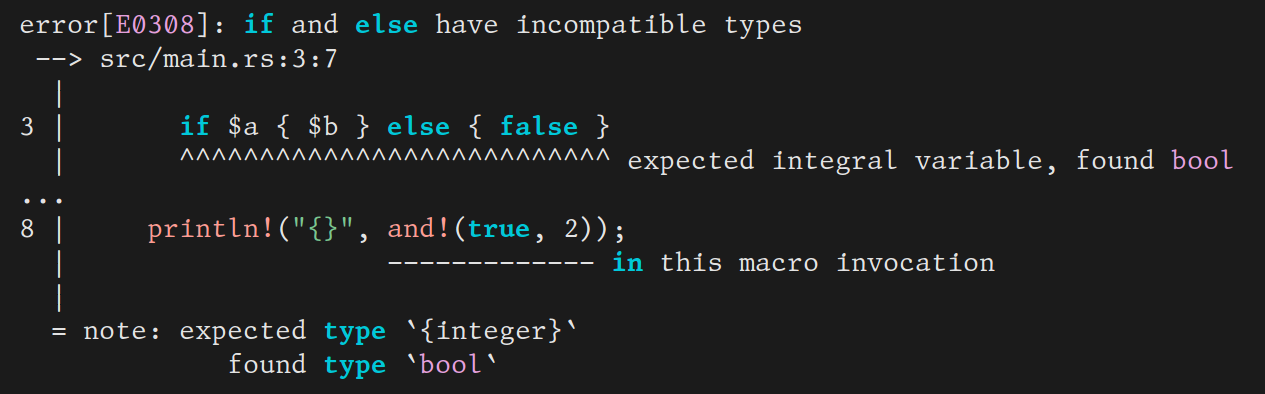
You can see that it shows you the definition of this macro. In this case it’s not so bad, but other macros can get messy, and you might not want to see their guts. Plus in principle, a type error should only show the erronous code, not correct code that it happend to call. You wouldn’t be very happy with a type checker that sometimes threw an error deep in the body of a (type correct) library function that you called, just because you used it the wrong way. Why put up with one that does the same thing for macros?

The reason Rust does is that that it does not know the type of and. As a result, it can only type check after and has been desugared (a.k.a., expanded), and so the error occurs in the desugared code.

But what if Rust could automatically infer a type rule for checking and, using only the its definition? Then the error could be found in the original program that you wrote (rather than its expansion), and presented as such. This is exactly what we did—albeit for simpler type systems than Rust’s—in our recent PLDI’18 paper Inferring Type Rules for Syntactic Sugar.

We call this process resugaring type rules; akin to our previous work on resugaring evaluation steps and resugaring scope rules. Let’s walk through the resugaring of a type rule for and:

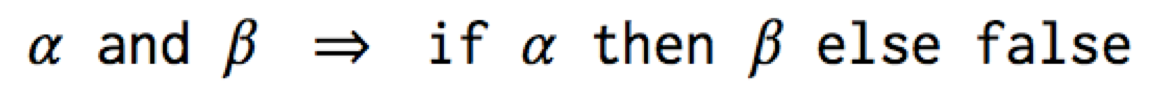
We want to automatically derive a type rule for and, and we want it to be correct. But what does it mean for it to be correct? Well, the meaning of and is defined by its desugaring: α and β is synonymous with if α then β else false. Thus they should have the same type:

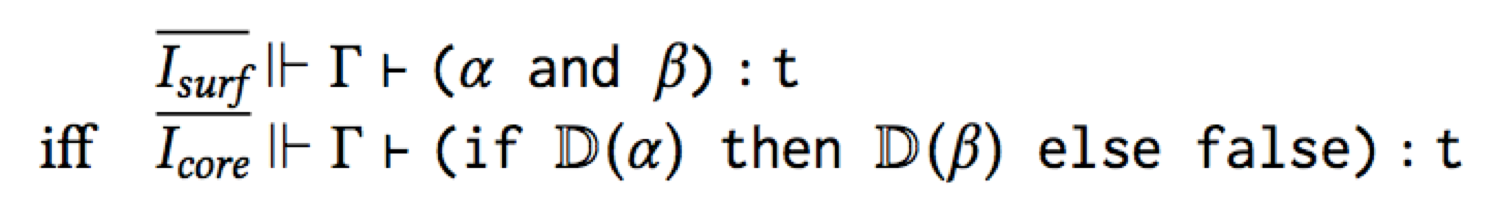
(Isurf ||- means “in the surface language type system”, Icore ||- means “in the core language type system”, and the fancy D means “desugar”.)

How can we achieve this? The most straightforward to do is to capture the iff with two type rules, one for the forward implication, and one for the reverse:

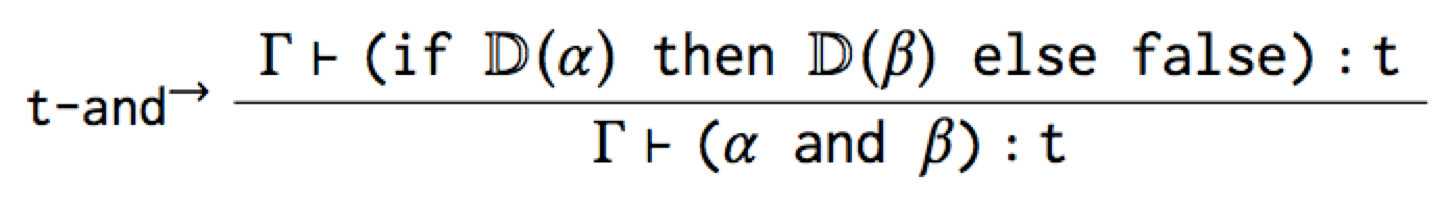
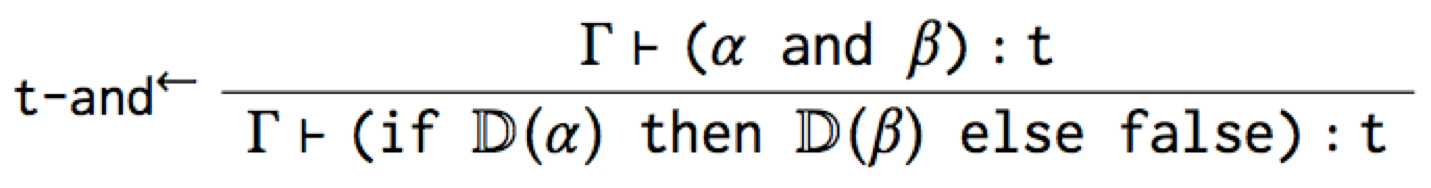
The first type rule is useful because it says how to type check and in terms of its desugaring. For example, here’s a derivation that true and false has type Bool:

However, while this t-and^→ rule is accurate, it’s not the canonical type rule for and that you’d expect. And worse, it mentions if, so it’s leaking the implementation of the macro!

However, we can automatically construct a better type rule. The trick is to look at a more general derivation. Here’s a generic type derivation for any term α and β:

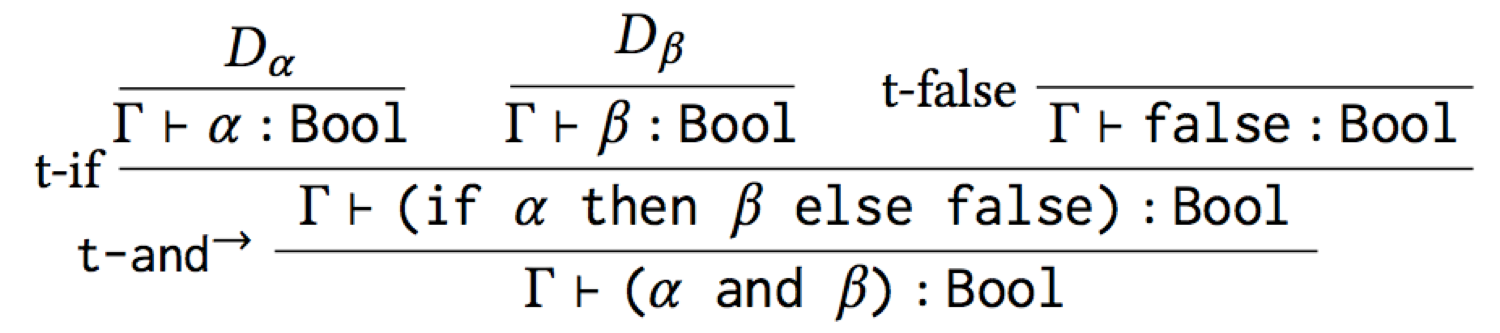
Notice D_α and D_β: these are holes in the derivation, which ought to be filled in with sub-derivations proving that α has type Bool and β has type Bool. Thus, “α : Bool” and “β : Bool” are assumptions we must make for the type derivation to work. However, if these assumptions hold, then the conclusion of the derivation must hold. We can capture this fact in a type rule, whole premises are these assumptions, and whose conclusion is the conclusion of the whole derivation:

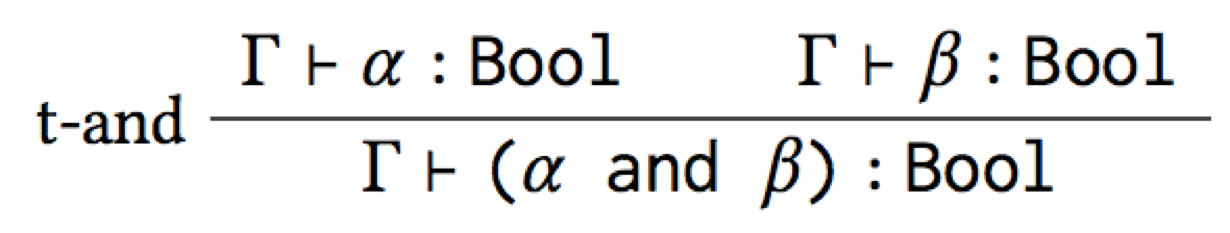
And so we’ve inferred the canonical type rule for and! Notice that (i) it doesn’t mention if at all, so it’s not leaking the inside of the macro, and (ii) it’s guaranteed to be correct, so it’s a good starting point for fixing up a type system to present errors at the right level of abstraction. This was a simple example for illustrative purposes, but we’ve tested the approach on a variety of sugars and type systems.

You can read more in our paper, or play with the implementation.

The Pyret Programming Language: Why Pyret?

Tags: Education, Programming Languages, Pyret, Semantics, Types

Posted on 26 June 2016.

We need better languages for introductory computing. A good introductory language makes good compromises between expressiveness and performance, and between simplicity and feature-richness. Pyret is our evolving experiment in this space.

Since we expect our answer to this question will evolve over time, we’ve picked a place for our case for the language to live, and will update it over time:

The Pyret Code; or A Rationale for The Pyret Programming Language

The first version answers a few questions that we expect many people have when considering languages in general and languages for education in particular:

Why not just use Java, Python, Racket, OCaml, or Haskell?
Will Pyret ever be a full-fledged programming language?
But there are lots of kinds of “education”!
What are some ways the educational philosophy influences the langauge?

In this post, it’s worth answering one more immediate question:

What’s going on right now, and what’s next?

We are currently hard at work on three very important features:

Support for static typing. Pyret will have a conventional type system with tagged unions and a type checker, resulting in straightforward type errors without the complications associated with type inference algorithms. We have carefully designed Pyret to always be typeable, but our earlier type systems were not good enough. We’re pretty happy with how this one is going.
Tables are a critical type for storing real-world data. Pyret is adding linguistic and library support for working effectively with tables, which PAPL will use to expose students to “database” thinking from early on.
Our model for interactive computation is based on the “world” model. We are currently revising and updating it in a few ways that will help it better serve our new educational programs.

On the educational side, Pyret is already used by the Bootstrap project. We are now developing three new curricula for Bootstrap:

A CS1 curriculum, corresponding to a standard introduction to computer science, but with several twists based on our pedagogy and materials.
A CS Principles curriculum, for the new US College Board Advanced Placement exam.
A physics/modeling curriculum, to help teach students physics and modeling through the medium of programming.

If you’d like to stay abreast of our developments or get involved in our discussions, please come on board!

Typechecking Uses of the jQuery Language

Tags: Browsers, JavaScript, Types

Posted on 17 January 2014.

Manipulating HTML via JavaScript is often a frustrating task: the APIs for doing so, known as the Document Object Model (or DOM), are implemented to varying degrees of fidelity across different browsers, leading to browser-specific workarounds that contort the code. Worse, the APIs are too low-level: they amount to an “assembly language for trees”, allowing programmers to navigate from a node to its parent, children or adjacent siblings; add, remove, or modify a node at a time; etc. And like assembly programming, these low-level operations are imperative and often error-prone.

Fortunately, developers have created libraries that abstract away from this low-level tedium to provide a powerful, higher-level API. The best-known example of these is jQuery, and its API is so markedly different from the DOM API that it might as well be its own language — a domain-specific language for HTML manipulation.

With great powerlanguage comes great responsibility

Every language has its own idiomatic forms, and therefore has its own characteristic failure modes and error cases. Our group has been studying various (sub-)languages of JavaScript— JS itself, ADsafety, private browsing violations— so the natural question to ask is, what can we do to analyze jQuery as a language?

This post takes a tour of the solution we have constructed to this problem. In it, we will see how a sophisticated technique, a dependent type system, can be specialized for the jQuery language in a way that:

Retains decidable type-inference,
Requires little programmer annotation overhead,
Hides most of the complexity from the programmer, and yet
Yields non-trivial results.

Engineering such a system is challenging, and is aided by the fact that jQuery’s APIs are well-structured enough that we can extract a workable typed description of them.

What does a jQuery program look like?

Let’s get a feel for those idiomatic pitfalls of jQuery by looking at a few tiny examples. We’ll start with a (seemingly) simple question: what does this one line of code do?

$(".tweet span").next().html()

With a little knowledge of the API, jQuery’s code is quite readable: get all the ".tweet span" nodes, get their next() siblings, and…get the HTML code of the first one of them. In general, a jQuery expression consists of three parts: a initial query to select some nodes, a sequence of navigational steps that select nearby nodes related to the currently selected set, and finally some manipulation to retrieve or set data on those node(s).

This glib explanation hides a crucial assumption: that there exist nodes in the page that match the initial selector in the first place! So jQuery programs’ behavior depends crucially on the structure of the pages in which they run.

Given the example above, the following line of code should behave analogously:

$(".tweet span").next().text()

But it doesn’t—it actually returns the concatenated text content of all the selected nodes, rather than just the first. So jQuery APIs have behavior that depends heavily on how many nodes are currently selected.

Finally, we might try to manipulate the nodes by mapping a function across them via jQuery’s each() method, and here we have a classic problem that appears in any language: we must ensure that the mapped function is only applied to the correct sorts of HTML nodes.

Our approach

The examples above give a quick flavor of what can go wrong:

The final manipulation might not be appropriate for the type of nodes actually in the query-set.
The navigational steps might “fall off the edge of the tree”, navigating by too many steps and resulting in a vacuous query-set.
The initial query might not match any nodes in the document, or match too many nodes.

Our tool of choice for resolving all these issues is a type system for JavaScript. We’ve used such a system before to analyze the security of Firefox browser extensions. The type system is quite sophisticated to handle JavaScript idioms precisely, and while we take advantage of that sophistication, we also completely hide the bulk of it from the casual jQuery programmer.

To adapt our prior system for jQuery, we need two technical insights: we define multiplicities, a new kind that allows us to approximate the size of a query set in its type and ensure that APIs are only applied to correctly-sized sets, and we define local structure, which allows developers to inform the type system about the query-related parts of the page.

Technical details

Multiplicities

Typically, when type system designers are confronted with the need to keep track of the size of a collection, they turn to a dependently typed system, where the type of a collection can depend on, say, a numeric value. So “a list of five booleans” has a distinct type from “a list of six booleans”. This is very precise, allowing some APIs to be expressed with exactitude. It does come at a heavy cost: most dependent type systems lose the ability to infer types, requiring hefty programmer annotations. But is all this precision necessary for jQuery?

Examining jQuery’s APIs reveals that its behavior can be broken down into five cases: methods might require their invocant query-set contain

Zero elements of any type T, writen 0<T>
One element of some type T, written 1<T>
Zero or one elements of some type T, written 01<T>
One or more elements of some type T, written 1+<T>
Any number (zero or more) elements of some type T, written 0+<T>

These cases effectively abstract the exact size of a collection into a simple, finite approximation. None of jQuery’s APIs actually care if a query set contains five or fifty elements; all the matters is that it contains one-or-more. And therefore our system can avoid the very heavyweight onus of a typical dependent type system, instead using this simpler abstraction without any loss of necessary precision.

Moreover, we can manipulate these cases using interval arithmetic: for example, combining one collection of zero-or-one elements with another collection containing exactly one element yields a collection of one-or-more elements: 01<T> + 1<T> = 1+<T>. This is just interval addition.

jQuery’s APIs all effectively map some behavior across a queryset. Consider the next() method: given a collection of at least one element, it transforms each element into at most one element (because some element might not have any next sibling). The result is a collection of zero-or-more elements (if every element does not have a next sibling). Symbolically: 1+<01<T>> = 0+<T>. This is just interval multiplication.

We can use these two operations to describe the types of all of jQuery’s APIs. For example, the next() method can be given the type Forall T, 1+<T> -> 0+<@next<T>>.

Local structure

Wait — what’s @next? Recall that we need to connect the type system to the content of the page. So we ask programmers to define local structures that describe the portions of their pages that they intend to query. Think of them as “schemas for page fragments”: while it is not reasonable to ask programmers to schematize parts of the page they neither control nor need to manipulate (such as 3^rd-party ads), they certainly must know the structure of those parts of the page that they query! A local structure for, say, a Twitter stream might say:

(Tweet : Div classes = {tweet} optional = {starred}
   (Author : Span classes = {span})
   (Time : Span classes = {time})
   (Content : Span classes = {content})

Read this as “A Tweet is a Div that definitely has class tweet and might have class starred. It contains three children elements in order: an Author, a Time, and a Content. An Author is a Span with class span…”

(If you are familiar with templating libraries like mustache.js, these local structures might look familiar: they are just the widgets you would define for template expansion.)

From these definitions, we can compute crucial relationships: for instance, the @next sibling of an Author is a Time. And that in turn completes our understanding of the type for next() above: for any local structure type T, next() can be called on a collection of at least one T and will return collection of zero or more elements that are the @next siblings of Ts.

Note crucially that while the uses of @next are baked into our system, the function itself is not defined once-and-for-all for all pages: it is computed from the local structures that the programmer defined. In this way, we’ve parameterized our type system. We imbue it with knowledge of jQuery’s fixed API, but leave a hole for programmers to provide their page-specific information, and thereby specialize our system for their code.

Of course, @next is not the only function we compute over the local structure. We can compute @parents, @siblings, @ancestors, and more. But all of these functions are readily deducible from the local structure.

Ok, so what does this all do for me?

Continuing with our Tweet example above, our system provides the following output for these next queries:

// Mistake made: one too many calls to .next(), so the query set is empty
$(".tweet").children().next().next().next().css("color", "red")
// ==> ERROR: 'css' expects 1+<Element>, got 0<Element>

// Mistake made: one too few calls to .next(), so the query set is too big
$(".tweet #myTweet").children().next().css("color")
// ==>; ERROR: 'css' expects 1<Element>, got 1+<Author+Time>

// Correct query
$(".tweet #myTweet").children().next().next().css("color")
// ==> Typechecks successfully

The paper contains additional examples, showing how the types progress across more elaborate jQuery expressions.

The big picture

We have defined a set of types for the jQuery APIs that captures their intended behavior. These types are expressed using helper functions such as @next, whose behavior is specific to each page. We ask programmers merely to define the local structures of their page, and from that we compute the helper functions we need. And finally, from that, our system can produce type errors whenever it encounters the problematic situations we listed above. No additional programmer effort is needed, and the type errors produced are typically local and pertinent to fixing buggy code.

Verifying Extensions' Compliance with Firefox's Private Browsing Mode

Tags: Browsers, JavaScript, Programming Languages, Security, Types, Verification

Posted on 19 August 2013.

All modern browsers now support a “private browsing mode”, in which the browser ostensibly leaves behind no traces on the user's file system of the user's browsing session. This is quite subtle: browsers have to handle caches, cookies, preferences, bookmarks, deliberately downloaded files, and more. So browser vendors have invested considerable engineering effort to ensure they have implemented it correctly.

Firefox, however, supports extensions, which allow third party code to run with all the privilege of the browser itself. What happens to the security guarantee of private browsing mode, then?

The current approach

Currently, Mozilla curates the collection of extensions, and any extension must pass through a manual code review to flag potentially privacy-violating behaviors. This is a daunting and tedious task. Firefox contains well over 1,400 APIs, of which about twenty are obviously relevant to private-browsing mode, and another forty or so are less obviously relevant. (It depends heavily on exactly what we mean by the privacy guarantee of “no traces left behind”: surely the browser should not leave files in its cache, but should it let users explicitly download and save a file? What about adding or deleting bookmarks?) And, if the APIs or definition of private-browsing policy ever change, this audit must be redone for each of the thousands of extensions.

The asymmetry in this situation should be obvious: Mozilla auditors should not have to reconstruct how each extension works; it should be the extension developers' responsibility to convince the auditor that their code complies with private-browsing guarantees. After all, they wrote the code! Moreover, since auditors are fallible people, too, we should look to (semi-)automated tools to lower their reviewing effort.

Our approach

So what property, ultimately, do we need to confirm about an extension's code to ensure its compliance? Consider the pseudo-code below, which saves the current preferences to disk every few minutes:

  var prefsObj = ...
  const thePrefsFile = "...";
  function autoSavePreferences() {
    if (inPivateBrowsingMode()) {
      // ...must store data only in memory...
      return;
    } else {
      // ...allowed to save data to disk...
      var file = openFile(thePrefsFile);
      file.write(prefsObj.tostring());
    }
  }
  window.setTimeout(autoSafePreferences, 3000);

The key observation is that this code really defines two programs that happen to share the same source code: one program runs when the browser is in private browsing mode, and the other runs when it isn't. And we simply do not care about one of those programs, because extensions can do whatever they'd like when not in private-browsing mode. So all we have to do is “disentangle” the two programs somehow, and confirm that the private-browsing version does not contain any file I/O.

Technical insight

Our tool of choice for this purpose is a type system for JavaScript. We've used such a system before to analyze the security of the ADsafe sandbox. The type system is quite sophisticated to handle JavaScript idioms precisely, but for our purposes here we need only part of its expressive power. We need three pieces: first, three new types; second, specialized typing rules; and third, an appropriate type environment.

We define one new primitive type: Unsafe. We will ascribe this type to all the privacy-relevant APIs.
We use union types to define Ext, the type of “all private-browsing-safe extensions”, namely: numbers, strings, booleans, objects whose fields are Ext, and functions whose argument and return types are Ext. Notice that Unsafe “doesn’t fit” into Ext, so attempting to use an unsafe function, or pass it around in extension code, will result in a type error.
Instead of defining Bool as a primitive type, we will instead define True and False as primitive types, and define Bool as their union.

We'll also add two specialized typing rules:

If an expression has some union type, and only one component of that union actually typechecks, then we optimistically say that the expression typechecks even with the whole union type. This might seem very strange at first glance: surely, the expression 5("true") shouldn't typecheck? But remember, our goal is to prevent privacy violations, and the code above will simply crash---it will never write to disk. Accordingly, we permit this code in our type system.
We add special rules for typechecking if-expressions. When the condition typechecks at type True, we only check the then-branch; when the condition typechecks at type False, we only check the else-branch. (Otherwise, we check both branches as normal.)

Finally, we add the typing environment which initializes the whole system:

We give all the privacy-relevant APIs the type Unsafe.
We give the API inPrivateBrowsingMode() the type True. Remember: we just don't care what happens when it's false!

Put together, what do all these pieces achieve? Because Unsafe and Ext are disjoint from each other, we can safely segregate any code into two pieces that cannot communicate with each other. By carefully initializing the type environment, we make Unsafe precisely delineate the APIs that extensions should not use in private browsing mode. The typing rules for if-expressions plus the type for inPrivateBrowsingMode() amount to disentangling the two programs from each other: essentially, it implements dead-code elimination at type-checking time. Lastly, the rule about union types makes the system much easier for programmers to use, since they do not have to spend any effort satisfying the typechecker about properties other than this privacy guarantee.

In short, if a program passes our typechecker, then it must not call any privacy-violating APIs while in private-browsing mode, and hence is safe. No audit needed!

Wait, what about exceptions to the policy?

Sometimes, extensions have good reasons for writing to disk even while in private-browsing mode. Perhaps they're updating their anti-phishing blacklists, or they implement a download-helper that saves a file the user asked for, or they are a bookmark manager. In such cases, there simply is no way for the code to typecheck. As in any type system, we provide a mechanism to break out of the type system: an unchecked typecast. We currently write such casts as cheat(T). Such casts must be checked by a human auditor: they are explicitly marking the places where the extension is doing something unusual that must be confirmed.

(In our original version, we took our cue from Haskell and wrote such casts as unsafePerformReview, but sadly that is tediously long to write.)

But does it work?

Yes.

We manually analyzed a dozen Firefox extensions that had already passed Mozilla's auditing process. We annotated the extensions with as few type annotations as possible, with the goal of forcing the code to pass the typechecker, cheating if necessary. These annotations found five extensions that violated the private-browsing policy: they could not be typechecked without using cheat, and the unavoidable uses of cheat pointed directly to where the extensions violated the policy.

(Sub)Typing First Class Field Names

Tags: Programming Languages, Semantics, Types

Posted on 10 December 2012.

This post picks up where a previous post left off, and jumps back into the action with subtyping.

Updating Subtyping

There are two traditional rules for subtyping records, historically known as width and depth subtyping. Width subtyping allows generalization by dropping fields; one record is a supertype of another if it contains a subset of the sub-record's fields at the same types. Depth subtyping allows generalization within a field; one record is a supertype of another if it is identical aside from generalizing one field to a supertype of the type in the same field in the sub-record.

We would like to understand both of these kinds of subtyping in the context of our first-class field names. With traditional record types, fields are either mentioned in the record or not. Thus, for each possible field in both types, there are four combinations to consider. We can describe width and depth subtyping in a table:

`T₁`	`T₂`	`T₁ <: T₂` if...
`f: S`	`f: T`	`S <: T`
`f: -`	`f: T`	Never
`f: S`	`f: -`	Always
`f: -`	`f: -`	Always

We read f: S as saying that T₁ has the field f with type S, and we read f: - as saying that the corresponding type doesn't mention the field f. The first row of the table corresponds to depth subtyping, where the field f is still present, but at a more general type in T₂. The second row is a failure to subtype, when T₂ has a field that isn't mentioned at all in T₁. The third row corresponds to width subtyping, where a field is dropped and not mentioned in the supertype. The last row is a trivial case, where neither type mentions the field.

For records with string patterns, we can extend this table with new combinations to account for ○ and ↓ annotations. The old rows remain, and become the ↓ cases, and new rows are added for ○ annotations:

`T₁`	`T₂`	`T₁ <: T₂` if...
`f^↓: S`	`f^↓: T`	`S <: T`
`f^○: S`	`f^↓: T`	Never
`f: -`	`f^↓: T`	Never
`f^↓: S`	`f^○: T`	`S <: T`
`f^○: S`	`f^○: T`	`S <: T`
`f: -`	`f^○: T`	Never
`f^↓: S`	`f: -`	Always
`f^○: S`	`f: -`	Always
`f: -`	`f: -`	Always

Here, we see that it is safe to treat a definitely present field as a possibly-present one, in the case where we compare f^↓:S to f^○:T). The dual of this case, treating a possibly-present field as definitely-present, is unsafe, as the comparison of f^○:S to f^↓:T shows. Possibly present annotations do not allow us to invent fields, as having f: - on the left-hand-side is still only permissible if the right-hand-side also doesn't mention f.

Giving Types to Values

In order to ascribe these rich types to object values, we need rules for typing basic objects, and then we need to apply these subtyping rules to generalize them. As a working example, one place where objects with field patterns come up every day in practice is in JavaScript arrays. Arrays in JavaScript hold their elements in fields named by stringified numbers. Thus, a simplified type for a JavaScript array of booleans is roughly:

BoolArrayFull: { [0-9]+^○: Bool }

That is, each field made up of a sequence of digits is possibly present, and if it is there, it has a boolean value. For simplicity, let's consider a slightly neutered version of this type, where only single digit fields are allowed:

BoolArray: { [0-9]^○: Bool }

Let's think about how we'd go about typing a value that should clearly have this type: the array [true, false]. We can think of this array literal as desugaring into an object like (indeed, this is what λJS does):

{"0": true, "1": false}

We would like to be able to state that this object is a member of the BoolArray type above. The traditional rule for record typing would ascribe a type mapping the names that are present to the types of their right hand side. Since the fields are certainly present, in our notation we can write:

{"0"^↓: Bool, "1"^↓: Bool}

This type should certainly be generalizable to BoolArray. That is, it should hold (using the rules in the table above) that:

{"0"^↓: Bool, "1"^↓: Bool} <: { [0-9]^○: Bool }

Let's see what happens when we instantiate the table for these two types:

`T₁`	`T₂`	`T₁ <: T₂` if...
`0^↓: Bool`	`0^○: Bool`	`Bool <: Bool`
`1^↓: Bool`	`1^○: Bool`	`Bool <: Bool`
`3: -`	`3^○: Bool`	Fail!
`4: -`	`4^○: Bool`	Fail!
...	...	...

(We cut off the table for 5-9, which are the same as the cases for 3 and 4). Our subtyping fails to hold for these types, which don't let us reflect the fact that the fields 3 and 4 are actually absent, and we should be allowed to consider them as possibly present at the boolean type. In fact, our straightforward rule for typing records is in fact responsible for throwing away this information! The type that it ascribed,

{"0"^↓: Bool, "1"^↓: Bool}

is actually the type of many objects, including those that happen to have fields like "banana" : 42. Traditional record typing drops fields when it doesn't care if they are present or absent, which loses information about definitive absence.

We extend our type language once more to keep track of this information. We add an explicit piece of a record type that tracks a description of the fields that are definitely absent on an object, and use this for typing object literals:

p = ○ | ↓
T = ... | { L^p : T ..., L_A: abs }

Thus, the new type for ["0": true, "1": false] would be:

{"0"^↓: Bool, "1"^↓: Bool, ("0"|"1"): abs}

Here, the overbar denotes regular-expression complement, and this type is expressing that all fields other than "0" and "1" are definitely absent.

Adding another type of field annotation requires that we again extend our table of subtyping options, so we now have a complete description with 16 cases:

`T₁`	`T₂`	`T₁ <: T₂` if...
`f^↓: S`	`f^↓: T`	`S <: T`
`f^○: S`	`f^↓: T`	Never
`f: abs`	`f^↓: T`	Never
`f: -`	`f^↓: T`	Never
`f^↓: S`	`f^○: T`	`S <: T`
`f^○: S`	`f^○: T`	`S <: T`
`f: abs`	`f^○: T`	Always
`f: -`	`f^○: T`	Never
`f^↓: S`	`f: abs`	Never
`f^○: S`	`f: abs`	Never
`f: abs`	`f: abs`	Always
`f: -`	`f: abs`	Never
`f^↓: S`	`f: -`	Always
`f^○: S`	`f: -`	Always
`f: abs`	`f: -`	Always
`f: -`	`f: -`	Always

We see that absent fields cannot be generalized to be definitely present (the abs to f^↓ case), but they can be generalized to be possibly present at any type. This is expressed in the case that compares f : abs to f^○: T, which always holds for any T. To see these rules in action, we can instantiate them for the array example we've been working with to ask a new question:

{"0"^↓: Bool, "1"^↓: Bool, ("0"|"1"): abs} <: { [0-9]^○: Bool }

And the table:

`T₁`	`T₂`	`T₁ <: T₂` if...
`0^↓: Bool`	`0^○: Bool`	`Bool <: Bool`
`1^↓: Bool`	`1^○: Bool`	`Bool <: Bool`
`3: abs`	`3^○: Bool`	OK!
`4: abs`	`4^○: Bool`	OK!
...	...	...
`9: abs`	`9^○: Bool`	OK!
`foo: abs`	`foo: -`	OK!
`bar: abs`	`bar: -`	OK!
...	...	...

There's two things that make this possible. First, it is sound to generalize the absent fields that are possibly present on the array type, because the larger type doesn't guarantee their presence either. Second, it is sound to generalize absent fields that aren't mentioned on the array type, because unmentioned fields can be present or absent with any type. The combination of these two features of our subtyping relation lets us generalize from particular array instances to the more general type for arrays.

Capturing the Whole Table

The tables above present subtyping on a field-by-field basis, and the patterns we considered at first were finite. In the last case, however, the pattern of “fields other than 0 and 1” was in fact infinite, and we cannot actually construct that infinite table to describe subtyping. The writeup and its associated proof document lay out an algorithmic version of the rules presented in the tables above, and also provides a proof of their soundness.

The writeup also discusses another interesting problem, which is the interaction between these pattern types and inheritance, where patterns on the child and parent objects may overlap in subtle ways. It goes further and discusses what happens in cases like JavaScript, where the field "__proto__" is an accessible member that has inheritance semantics. Check it all out here!

Typing First Class Field Names

Tags: Programming Languages, Semantics, Types

Posted on 03 December 2012.

In a previous post, we discussed some of the powerful features of objects in scripting languages. One feature that stood out was the use of first-class strings as member names for objects. That is, in programs like

var o = {name: "Bob", age: 22};
function lookup(f) {
  return o[f];
}
lookup("name");
lookup("age");

the name position in field lookup has been abstracted over. Presumably only a finite set of names actually works with the lookup (o appears to only have two fields, after all).

It turns out that so-called “scripting” languages aren't the only ones that compute fields for lookup. For example, even within the constraints of Java's type system, the Bean framework computes method names to call at runtime. Developers can provide information about the names of fields and methods on a Bean with a BeanInfo instance, but even if they don't provide complete information, “the rest will be obtained by automatic analysis using low-level reflection of the bean classes’ methods and applying standard design patterns.” These “standard design patterns” include, for example, concatenating the strings "get" and "set" onto field names to produce method names to invoke at runtime.

Traditional type systems for objects and records have little to say about these computed accesses. In this post, we're going to build up a description of object types that can describe these values, and explore their use. The ideas in this post are developed more fully in a writeup for the FOOL Workshop.

First-class Singleton Strings

In the JavaScript example above, we said that it's likely that the only intended lookup targets―and thus the only intended arguments to lookup―are "name" and "age". Giving a meaningful type to this function is easy if we allow singleton strings as types in their own right. That is, if our type language is:

T = s | Str | Num
  | { s : T ... } | T → T | T ∩ T

Where s stands for any singleton string, Str and Num are base types for strings and numbers, respectively, record types are a map from singleton strings s to types, arrow types are traditional pairs of types, and intersections are allowed to express a conjunction of types on the same value.

Given these definitions, we could write the type of lookup as:

lookup : ("name" → Str) ∩ ("age" → Num)

That is, if lookup is provided the string "name", it produces a string, and if it is provided the string "age", it produces a number.

In order to type-check the body of lookup, we need a type for o as well. That can be represented with the type { "name" : Str, "age" : Num }. Finally, to type-check the object lookup expression o[f], we need to compare the singleton string type of f with the fields of o. In this case, only the two strings that are already present on o are possible choices for f, so the comparison is easy and type-checking works out.

For a first cut, all we did was make the string labels on objects' fields a first-class entity in our type system, with singleton string types s. But what can we say about the Bean example, where get* and set* method invocations are computed rather than just used as first-class values?

String Pattern Types

In order to express the type of objects like Beans, we need to express field name patterns, rather than just singleton field names. For example, we might say that a Bean with Int-typed parameters has a type like:

IntBean = { ("get".+)  : → Int },
            ("set".+)  : Int → Void,
            "toString" : → Str }

Here, we are using .+ as regular expression notation for any non-empty string. We read the type above as saying that all fields that begin with get and end with any string are functions that return Int values. The same is true for "set" methods. The singleton string "toString" is also a field, and is simply a function that returns strings.

To express this type, we need to extend our type language to handle these string patterns, which we write down as regular expressions (the write-up outlines the actual limits on what kinds of patterns we can support). We extend our type language to include patterns as types, and as field names:

L = regular expressions
T = L | Str | Num
  | { L : T ... } | T → T | T ∩ T

This new specification gives us the ability to write down types like IntBean, which have field patterns that describe infinite sets of fields. Let's stop and think about what that means as a description of a runtime object. Our type for o above, { "name" : Str, "age" : Num }, says that values bound to o at runtime certainly have name and age fields at the listed types. The type for IntBean, on the other hand, seems to assert that these objects will have the fields getUp, getDown, getSerious, and infinitely more. But a runtime object can't actually have all of those fields, so a pattern indicating an infinite number of field names is describing a fundamentally different kind of value.

What an object type with an infinite pattern represents is that all the fields that match the pattern are potentially present. That is, at runtime, they may or may not be there, but if they are there, they must have the annotated type. We extend object types again to make this explicit with presence annotations, which explicitly list fields as definitely present, written ↓, or possibly present, written ○:

p = ○ | ↓
T = ... | { L^p : T ... }

In this notation, we would write:

IntBean = { ("get".+)^○  : → Int },
            ("set".+)^○  : Int → Void,
            "toString"^↓ : → Str }

Which indicates that all the fields in ("get".+) and ("set".+) are possibly present with the given arrow types, and toString is definitely present.

Subtyping

Now that we have these rich object types, it's natural to ask what kinds of subtyping relationships they have with one another. A detailed account of subtyping will come soon; in the meantime, can you guess what subtyping might look like for these types?

Update: The answer is in the next post.

Progressive Types

Tags: Programming Languages, Semantics, Types

Posted on 01 September 2012.

Adding types to untyped languages has been studied extensively, and with good reason. Type systems offer developers strong static guarantees about the behavior of their programs, and adding types to untyped code allows developers to reap these benefits without having to rewrite their entire code base. However, these guarantees come at a cost. Retrofitting types on to untyped code can be an onerous and time-consuming process. In order to mitigate this cost, researchers have developed methods to type partial programs or sections of programs, or to allow looser guarantees from the type system. (Gradual typing and soft typing are some examples.) This reduces the up-front cost of typing a program.

However, these approaches only address a part of the problem. Even if the programmer is willing to expend the effort to type the program, he still cannot control what counts as an acceptable program; that is determined by the type system. This significantly reduces the flexibility of the language and forces the programmer to work within a very strict framework. To demonstrate this, observe the following program in Racket...

#lang racket

(define (gt2 x y)
  (> x y))

...and its Typed Racket counterpart.

#lang typed/racket

(: gt2 (Number Number -> Boolean))
(define (gt2 x y)
  (> x y))

The typed example above, which appears to be logically typed, fails to type-check. This is due to the sophistication with which Typed Racket handles numbers. It can distinguish between complex numbers and real numbers, integers and non-integers, even positive and negative integers. In this system, Number is actually an alias for Complex. This makes sense in that complex numbers are in fact the super type of all other numbers. However, it would also be reasonable to assume that Number means Real, because that's what people tend to think of when they think “number”. Because of this, a developer may expect all functions over real numbers to work over Numbers. However, this is not the case. Greater-than, which is defined over reals, cannot be used with Number because it is not defined over complex numbers. Now, this could be resolved by changing the type of gt2 to take Reals, rather than Numbers. But then consider this program:

#lang typed/racket

(: plus (Number Number -> Number))
(define (plus x y)
  (+ x y))
;Looks fine so far...

(: gt2 (Real Real -> Boolean))
(define (gt2 x y)
  (> x y))
;...Still ok...

(gt2 (plus 3 4) 5)
;...Here (plus 3 4) evaluates to a Number which causes gt2 to give 
;the type error “Expected Real but got Complex”.

Now, in order to make this program type, we would have to adjust plus to return Reals, even though it works with it's current typing! And we'd have to do the same for every program that calls plus. This can cause a ripple effect through the program, making typing the program labor-intensive, despite the fact that the program will actually run just fine on some inputs, which may be all we care about. But we still have to jump through hoops to get the program to run at all!

In the above example, the type system in Typed Racket requires the programmer to ensure that there are no runtime errors caused by using a complex number where a real number is expected, even if it means significant extra programming effort. There are cases, however, where type systems do not provide guarantees because it would cross the threshold of too much work for programmers. One such guarantee is ensuring that vector references are always given positive integer inputs. The Typed Racket type system does not offer this guarantee because of the required programming effort, and so it traded that particular guarantee for convenience and ease of programming.

In both these cases, type systems are trying to determine the best balance betwen safety and convenience. However, the best a system can do is choose either safety or convenience and apply that to all programs. Vector references cannot be checked in any program, because it isn't worth the extra engineering effort, whereas all programs must be checked for number realness, because it's worth the extra engineering effort. This seems pretty arbirtary! Type systems are trying to guess at what the developer might want, instead of just asking. However, the developer has a much better idea of which checks are relevant and important for a specific program and which are irrelevant or unimportant. The type system should leverage this information and offer the useful guarantees without requiring unhelpful ones.

Progressive Types

To this end, we have developed progressive types, which allow the developer to require type guarantees that are significant to the program, and ignore those that are irrelevant. From the total set of possible type errors, the developer would select which among them must be detected as compile time type errors, and which should be allowed to possibly cause runtime failures. In the above example, the developer could allow errors caused by treating a Number as a Real at runtime, trusting that they will never occur or that it won't be catastrophic if they do or that the particular error is orthogonal to the reasons for type-checking the program at all. Thus, the developer can disregard an insignificant error while still reaping the benefits of the rest of the type system. This addresses a problem that underlies all type systems: The programmer doesn't get to choose which classes of programs are “good” and which are “bad.” Progressive types give the programmer that control.

In order to allow this, the type system has an allowed error set, Ω, in addition to the type environment. So while a traditional typing rule takes the form Γ⊢e:τ, a rule in progressive type would take the form Ω;Γ⊢e:τ. Here, Ω is the set of errors the developer wants to allow to cause runtime failures. Expressions may evaluate to errors, and if those errors are in Ω, the expression will type to ⊥, otherwise it will fail to type. This is reflected in the progress theorem that goes along with the type system.

If Typed Racket were a progressively typed language, the above program would type only if the programmer had selected “Expected Real, but got Complex” to be in Ω. This means that if numerical calculations are really orthogonal to the point of the program, or there are other checks in place insuring the function will only get the right type of input, the developer can just tell the type checker not to worry about those errors! However, if it's important to ensure that complex numbers never appear where reals are required, the developer can tell the type checker to detect those errors. Thus the programmer can determine what constitutes a “good” program, rather than working around a different, possibly inconvenient, definition of “good”. By passing this control over to the developer, progressive type systems allow the balance between ease of engineering and saftey to be set at a level appropriate to the program.

Progressive typing differs from gradual typing in that while gradual typing allows the developer to type portions of a program with a fixed type system, progressive types instead allow the developer to vary the guarantees offered by the type system. Further, like soft typing, progressive typing allows for runtime errors instead of static guarantees, but unlike soft typing, it restricts which classes of runtime failures are allowed to occur. Because our system allows programmers to progressively adjust the restrictions imposed by the type system, either to loosen or tighten them, they can reap many of the flexibility benefits of a dynamic languages, but get static guarantees of a type system in the way best suited to each of their programs or preferences.

If you are interested in learning more about progressive types, look here.

ADsafety

Tags: Browsers, JavaScript, Programming Languages, Security, Types, Verification

Posted on 13 September 2011.

A mashup is a webpage that mixes and mashes content from various sources. Facebook apps, Google gadgets, and various websites with embedded maps are obvious examples of mashups. However, there is an even more pervasive use case of mashups on the Web. Any webpage that displays third-party ads is a mashup. It's well known that third-party content can include third-party cookies; your browser can even block these if you're concerned about "tracking cookies". However, third party content can also include third-party JavaScript that can do all sorts of wonderful and malicious things (just some examples).

Is it possible to safely embed untrusted JavaScript on a page? Google Caja, Microsoft Web Sandbox, and ADsafe are language-based Web sandboxes that try to do so. Language-based sandboxing is a programming language technique that restricts untrusted code using static and runtime checks and rewriting potential dangerous calls to safe, trusted functions.

Sandboxing JavaScript, with all its corner cases, is particularly hard. A single bug can easily break the entire sandboxing system. JavaScript sandboxes do not clearly state their intended guarantees, nor do they clearly argue why they are safe.

Verifying Web Sandboxes

A year ago, we embarked on a project to verify ADsafe, Douglas Crockford's Web sandbox. ADsafe is admittedly the simplest of the aforementioned sandboxes. But, we were also after the shrimp bounty that Doug offers for sandbox-breaking bugs:

Write a program [...] that calls the alert function when run on any browser. If the program produces no errors when linted with the ADsafe option, then I will buy you a plate of shrimp. (link)

A year later, we've produced a USENIX Security paper on our work, which we presented in San Francisco in August. The paper discusses the many common techniques employed by Web sandboxes and discusses the intricacies of their implementations. (TLDR: JavaScript and the DOM are really hard.) Focusing on ADsafe, it precisely states what ADsafety actually means. The meat of the paper is our approach to verifying ADsafe using types. Our verification leverages our earlier work on semantics and types for JavaScript, and also introduces some new techniques:

Check out the ★s and ☠s in our object types; we use them to type-check "scripty" features of JavaScript. ☠ marks a field as "banned" and ★ specifies the type of all other fields.
We also characterize JSLint as a type-checker. The Widget type presented in the paper specifies, in 20 lines, the syntactic restrictions of JSLint's ADsafety checks.

Unlike conventional type systems, ours does not prevent runtime errors. After all, stuck programs are safe because they trivially don't execute any code. If you think type systems only catch "method not found" errors, you should have a look at ours.

We found bugs in both ADsafe and JSLint that manifested as type errors. We reported all of them and they were promptly fixed by Doug Crockford. A big thank you to Doug for his encouragement, for answering our many questions, and for buying us every type of shrimp dish in the house.

Doug Crockford, Joe, Arjun, and seven shrimp dishes

Learn more about ADsafety! Check out:

The paper, code, and proofs;
Video of Arjun presenting at USENIX Security;
ADsafe and JSLint.

The Brown PLT Blog

Articles by tag: Types

Tables are Everywhere

(Typed) Programming with Tables

Making Results Comparable

Do Now!

Benchmark Components

An Open Process

For More Details

What’s going on right now, and what’s next?

With great powerlanguage comes great responsibility

What does a jQuery program look like?

Our approach

Technical details

Multiplicities

Local structure

Ok, so what does this all do for me?

The big picture

Further reading

The current approach

Our approach

Technical insight

Wait, what about exceptions to the policy?

But does it work?

Further reading

Updating Subtyping

Giving Types to Values

Capturing the Whole Table

First-class Singleton Strings

String Pattern Types

Subtyping

Progressive Types

Verifying Web Sandboxes