Can We Crowdsource Language Design?

Tags: Programming Languages, User Studies, Semantics

Posted on 06 July 2017.

Programming languages are user interfaces. There are several ways of making decisions when designing user interfaces, including:

a small number of designers make all the decisions, or
user studies and feedback are used to make decisions.

Most programming languages have been designed by a Benevolent Dictator for Life or a committee, which corresponds to the first model. What happens if we try out the second?

We decided to explore this question. To get a large enough number of answers (and to engage in rapid experimentation), we decided to conduct surveys on Amazon Mechanical Turk, a forum known to have many technically literate people. We studied a wide range of common programming languages features, from numbers to scope to objects to overloading behavior.

We applied two concrete measures to the survey results:

Consistency: whether individuals answer similar questions the same way, and
Consensus: whether we find similar answers across individuals.

Observe that a high value of either one has clear implications for language design, and if both are high, that suggests we have zeroed in on a “most natural” language.

As Betteridge’s Law suggests, we found neither. Indeed,

A surprising percentage of workers expected some kind of dynamic scope (83.9%).
Some workers thought that record access would distribute over the field name expression.
Some workers ignored type annotations on functions.
Over the field and method questions we asked on objects, no worker expected Java’s semantics across all three.

These and other findings are explored in detail in our paper.

A Third Perspective on Hygiene

Tags: Programming Languages, Semantics

Posted on 20 June 2017.

In the last post, we talked about scope inference: automatically inferring scoping rules for syntatic sugar. In this post we’ll talk about the perhaps surprising connection between scope inference and hygiene.

Hygiene can be viewed from a number of perspectives and defined in a number of ways. We’ll talk about two pre-existing perspectives, and then give a third perspective that comes from having scope inference.

First Perspective

The traditional perspective on hygiene (going all the way back to Kohlbecker in ’86) defines it by what shouldn’t happen when you expand macros / syntactic sugar. To paraphrase the idea:

Expanding syntactic sugar should not cause accidental variable capture. For instance, a variable used in a sugar should not come to refer to a variable declared in the program simply because it has the same name.

Thus, hygiene in this tradition is defined by a negative.

It has also traditionally focused strongly on algorithms. One would expect papers on hygiene to state a definition of hygiene, give an algorithm for macro expansion, and then prove that the algorithm obeys these properties. But this last step, the proof, is usually suspiciously missing. At least part of the reason for this, we suspect, is that definitions of hygiene have been too informal to be used in a proof.

And a definition of hygiene has been surprisingly hard to pin down precisely. In 2015, a full 29 years after Kohlbecker’s seminal work, Adams writes that “Hygiene is an essential aspect of Scheme’s macro system that prevents unintended variable capture. However, previous work on hygiene has focused on algorithmic implementation rather than precise, mathematical definition of what constitutes hygiene.” He goes on to discuss “observed-binder hygiene”, which is “not often discussed but is implicitly averted by traditional hygiene algorithms”. The point we’re trying to make is that the traditional view on hygiene is subtle.

Second Perspective

There is a much cleaner definition of hygiene, however, that is more of a positive statement (and subsumes the preceding issues):

If two programs are α-equivalent (that is, they are the same up to renaming variables), then when you desugar them (that is, expand their sugars) they should still be α-equivalent.

Unfortunately, this definition only makes sense if we have scope defined on both the full and base languages. Most hygiene systems can’t use this definition, however, because the full language is not usually given explicit scoping rules; rather, it’s defined implicitly through translation into the base language.

Recently, Herman and Wand have advocated for specifying the scoping rules for the full language (in addition to the base language), and then verifying that this property holds. If the property doesn’t hold, then either the scope specification or the sugar definitions are incorrect. This is, however, an onerous demand to place on the developer of syntactic sugar, especially since scope can be surprisingly tricky to define precisely.

Third Perspective

Scope inference gives a third perspective. Instead of requiring authors of syntactic sugar to specify the scoping rules for the full language, we give an algorithm that infers them. We have to then define what it means for this algorithm to work “correctly”.

We say that an inferred scope is correct precisely if the second definition of hygiene holds: that is, if desugaring preserves α-equivalence. Thus, our scope inference algorithm finds scoping rules such that this property holds, and if no such scoping rules exist then it fails. (And if there are multiple sets of scoping rules to choose from, it chooses the ones that put as few names in scope as possible.)

An analogy would be useful here. Think about type inference: it finds type annotations that could be put in your program such that it would type check, and if there are multiple options then it picks the most general one. Scope inference similarly finds scoping rules for the full language such that desugaring preserves α-equivalence, and if there are multiple options then it picks the one that puts the fewest names in scope.

This new perspective on hygiene allows us to shift the focus from expansion algorithms to the sugars themselves. When your focus is on an expansion algorithm, you have to deal with whatever syntactic sugar is thrown your way. If a sugar introduces unbound identifiers, then the programmer (who uses the macro) just has to deal with it. Likewise, if a sugar uses scope inconsistently, treating a variable either as a declaration or a reference depending on the phase of the moon, the programmer just has to deal with it. In contrast, since we infer scope for the full language, we check check weather a sugar would do one of these bad things, and if so we can call the sugar unhygienic.

To be more concrete, consider a desugaring rule for bad(x, expression) that sometimes expands to lambda x: expression and sometimes expands to just expression, depending on the context. Our algorithm would infer from the first rewrite that the expression must be in scope of x. However, this would mean that the expression was allowed to contain references to x, which would become unbound when the second rewrite was used! Our algorithm detects this and rejects this desugaring rule. Traditional macro systems allow this, and only detect the potential unbound identifier problem when it actually occurred. The paper contains a more interesting example called “lambda flip flop” that is rejected because it uses scope inconsistently.

Altogether, scope inference rules out bad sugars that cannot be made hygienic, but if there is any way to make a sugar hygienic it will find it.

Again, here’s the paper and implementation, if you want to read more or try it out.

Scope Inference, a.k.a. Resugaring Scope Rules

Tags: Programming Languages, Semantics

Posted on 12 June 2017.

This is the second post in a series about resugaring. It focuses on resugaring scope rules. See also our posts on resugaring evaluation steps and resugaring type rules.

Many programming languages have syntactic sugar. We would hazard to guess that most modern languages do. This is when a piece of syntax in a language is defined in terms of the rest of the language. As a simple example, x += expression might be shorthand for x = x + expression. A more interesting sugar is Pyret’s for loops. For example:

for fold(p from 1, n from range(1, 6)):
  p * n
end

computes 5 factorial, which is 120. This for is a piece of sugar, though, and the above code is secretly shorthand for:

fold(lam(p, n): p * n end, 1, range(1, 6))

Sugars like this are great for language development: they let you grow a language without making it more complicated.

Languages also have scoping rules that say where variables are in scope. For instance, the scoping rules should say that a function’s parameters are in scope in the body of the function, but not in scope outside of the function. Many nice features in editors depend on these scoping rules. For instance, if you use autocomplete for variable names, it should only suggest variables that are in scope. Similarly, refactoring tools that rename variables need to know what is in scope.

This breaks down in the presence of syntactic sugar, though: how can your editor tell what the scoping rules for a sugar are?

The usual approach is to write down all of the scoping rules for all of the sugars. But this is error prone (you need to make sure that what you write down matches the actual behavior of the sugars), and tedious. It also goes against a general principle we hold: to add a sugar to a language, you should just add the sugar to the language. You shouldn’t also need to update your scoping rules, or update your type system, or update your debugger: that should all be done automatically.

We’ve just published a paper at ICFP that shows how to automatically infer the scoping rules for a piece of sugar, like the for example above. Here is the paper and implementation. This is the latest work we’ve done with the goal of making the above principle a reality. Earlier, we showed how to automatically find evaluation steps that show how your program runs in the presence of syntatic sugar.

How it Works

Our algorithm needs two things to run:

The definitions of syntactic sugar. These are given as pattern-based rewrite rules, saying what patterns match and what they should be rewritten to.
The scoping rules for the base (i.e. core) language.

It then automatically infers scoping rules for the full language, that includes the sugars. The final step to make this useful would be to add these inferred scoping rules to editors that can use them, such as Sublime, Atom, CodeMirror, etc.

For example, we have tested it on Pyret (as well as other languages). We gave it scoping rules for Pyret’s base language (which included things like lambdas and function application), and we gave it rules for how for desugars, and it determined the scoping rules of for. In particular:

The variables declared in each from clause are visible in the body, but not in the argument of any from clause.
If two from clauses both declare the same variable, the second one shadows the first one.

This second rule is exactly the sort of thing that is easy to overlook if you try to write these rules down by hand, resulting in obscure bugs (e.g. when doing automatic variable refactoring).

Here are the paper and implementation, if you want to read more or try it out.

The Pyret Programming Language: Why Pyret?

Tags: Education, Programming Languages, Semantics

Posted on 26 June 2016.

We need better languages for introductory computing. A good introductory language makes good compromises between expressiveness and performance, and between simplicity and feature-richness. Pyret is our evolving experiment in this space.

Since we expect our answer to this question will evolve over time, we’ve picked a place for our case for the language to live, and will update it over time:

The Pyret Code; or A Rationale for The Pyret Programming Language

The first version answers a few questions that we expect many people have when considering languages in general and languages for education in particular:

Why not just use Java, Python, Racket, OCaml, or Haskell?
Will Pyret ever be a full-fledged programming language?
But there are lots of kinds of “education”!
What are some ways the educational philosophy influences the langauge?

In this post, it’s worth answering one more immediate question:

What’s going on right now, and what’s next?

We are currently hard at work on three very important features:

Support for static typing. Pyret will have a conventional type system with tagged unions and a type checker, resulting in straightforward type errors without the complications associated with type inference algorithms. We have carefully designed Pyret to always be typeable, but our earlier type systems were not good enough. We’re pretty happy with how this one is going.
Tables are a critical type for storing real-world data. Pyret is adding linguistic and library support for working effectively with tables, which PAPL will use to expose students to “database” thinking from early on.
Our model for interactive computation is based on the “world” model. We are currently revising and updating it in a few ways that will help it better serve our new educational programs.

On the educational side, Pyret is already used by the Bootstrap project. We are now developing three new curricula for Bootstrap:

A CS1 curriculum, corresponding to a standard introduction to computer science, but with several twists based on our pedagogy and materials.
A CS Principles curriculum, for the new US College Board Advanced Placement exam.
A physics/modeling curriculum, to help teach students physics and modeling through the medium of programming.

If you’d like to stay abreast of our developments or get involved in our discussions, please come on board!

Resugaring Evaluation Sequences

Tags: Programming Languages, Semantics

Posted on 06 February 2016.

This is the first post in a series about resugaring. It focuses on resugaring evaluation sequences. See also our later posts on resugaring scope rules and resugaring type rules.

A lot of programming languages are defined in terms of syntactic sugar. This has many advantages, but also a couple of drawbacks. In this post, I’m going to tell you about one of these drawbacks, and the solution we found for it. First, though, let me describe what syntactic sugar is and why it’s used.

Syntactic sugar is when you define a piece of syntax in a language in terms of the rest of the language. You’re probably already familiar with many examples. For instance, in Python, x + y is syntactic sugar for x.__add__(y). I’m going to use the word “desugaring” to mean the expansion of syntactic sugar, so I’ll say that x + y desugars to x.__add__(y). Along the same lines, in Haskell, [f x | x <- lst] desugars to map f lst. (Well, I’m simplifying a little bit; the full desugaring is given by the Haskell 98 spec.)

As a programming language researcher I love syntactic sugar, and you should too. It splits a language into two parts: a big “surface” language that has the sugar, and a much smaller “core” language that lacks it. This separation lets programmers use the surface language that has all of the features they know and love, while letting tools work over the much simpler core language, which lets the tools themselves be simpler and more robust.

There’s a problem, though (every blog post needs a problem). What happens when a tool, which has been working over the core language, tries to show code to the programmer, who has been working over the surface? Let’s zoom in on one instance of this problem. Say you write a little snippet of code, like so: (This code is written in an old version of Pyret; it should be readable even if you don’t know the language.)

my-list = [2]
cases(List) my-list:
  | empty() => print("empty")
  | link(something, _) =>
    print("not empty")
end

And now say you’d like to see how this code runs. That is, you’d like to see an evaluation sequence (a.k.a. an execution trace) of this program. Or maybe you already know what it will do, but you’re teaching students, and would like to show them how it will run. Well, what actually happens when you run this code is that it is first desugared into the core, like so:

my-list = list.["link"](2, list.["empty"])
block:
  tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({
    "empty" : fun(): print("empty") end,
    "link" : fun(something, _):
      print("not empty") end
},
fun(): raise("cases: no cases matched") end)
end

This core code is then run (each block of code is the next evaluation step):

my-list = obj.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = obj.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, obj.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, obj.["empty"])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = <func>(2, [])
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

my-list = [2]
block:
tempMODRIOUJ :: List = my-list
  tempMODRIOUJ.["_match"]({"empty" : fun():   print("empty") end,
  "link" : fun(something, _):   print("not empty") end}, fun():
  raise("cases: no cases matched") end)
  end

tempMODRIOUJ :: List = [2]
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)

[2].["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)

[2].["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)

<func>({"empty" : fun(): end, "link" : fun(something, _): print("not
empty") end}, fun(): raise("cases: no cases matched") end)

<func>({"empty" : fun(): end, "link" : fun(): end}, fun():
raise("cases: no cases matched") end)

<func>(obj, fun(): raise("cases: no cases matched") end)

<func>(obj, fun(): end)

<func>("not empty")

"not empty"

But that wasn’t terribly helpful, was it? Sometimes you want to see exactly what a program is doing in all its gory detail (along the same lines, it’s occasionally helpful to see the assembly code a program is compiling to), but most of the time it would be nicer if you could see things in terms of the syntax you wrote the program with! In this particular example, it would be much nicer to see:

my-list = [2]
cases(List) my-list:
  | empty() => print("empty")
  | link(something, _) =>
    print("not empty")
end

my-list = [2]
cases(List) my-list:
  | empty() => print("empty")
  | link(something, _) =>
    print("not empty")
end

cases(List) [2]:
| empty() => print("empty")
| link(something, _) =>
  print("not empty")
end

<func>("not empty")

"not empty"

(You might have noticed that the first step got repeated for what looks like no reason. What happened there is that the code [2] was evaluated to an actual list, which also prints itself as [2].)

So we built a tool that does precisely this. It turns core evaluation sequences into surface evaluation sequences. We call the process resugaring, because it’s the opposite of desugaring: we’re adding the syntactic sugar back into your program. The above example is actual output from the tool, for an old version of Pyret. I’m currently working on a version for modern Pyret.

Resugaring Explained

I always find it helpful to introduce a diagram when explaining resugaring. On the right is the core evaluation sequence, which is the sequence of steps that the program takes when it actually runs. And on the left is the surface evaluation sequence, which is what you get when you try to resugar each step in the core evaluation sequence. As a special case, the first step on the left is the original program.

Here’s an example. The starting program will be not(true) or true, where not is in the core language, but or is defined as a piece of sugar:

x or y    ==desugar==>  let t = x in
                          if t then t else y

And here’s the diagram:

The steps (downarrows) in the core evaluation sequence are ground truth: they are what happens when you actually run the program. In contrast, the steps in the surface evaluation sequence are made up; the whole surface evaluation sequence is an attempt at reconstructing a nice evaluation sequence by resugaring each of the core steps. Notice that the third core term fails to resugar. This is because there’s no good way to represent it in terms of or.

Formal Properties of Resugaring

It’s no good to build a tool without having a precise idea of what it’s supposed to do. To this end, we came up with three properties that (we think) capture exactly what it means for a resugared evaluation sequence to be correct. It will help to look at the diagram above when thinking about these properties.

Emulation says that every term on the left should desugar to the term to its right. This expresses the idea that the resugared terms can’t lie about the term they’re supposed to represent. Another way to think about this is that desugaring and resugaring are inverses.
Abstraction says that the surface evaluation sequence on the left should show a sugar precisely when the programmer used it. So, for example, it should show things using or and not let, because the original program used or but not let.
Coverage says that you should show as many steps as possible. Otherwise, technically the surface evaluation sequence could just be empty! That would satisfy both Emulation and Abstraction, which only say things about the steps that are shown.

We’ve proved that our resugaring algorithm obeys Emulation and Abstraction, and given some good emperical evidence that it obeys Coverage too.

I’ve only just introduced resugaring. If you’d like to read more, see the paper, and the followup that deals with hygiene (e.g., preventing variable capture).

Slimming Languages by Reducing Sugar

Tags: JavaScript, Programming Languages, Semantics

Posted on 08 January 2016.

JavaScript is a crazy language. It’s defined by 250 pages of English prose, and even the parts of the language that ought to be simple, like addition and variable scope, are very complicated. We showed before how to tackle this problem using λ_s5, which is an example of what’s called a tested semantics.

You can read about λ_s5 at the above link. But the basic idea is that λ_s5 has two parts:

A small core language that captures the essential parts of JavaScript, without all of its foibles, and
A desugaring function that translates the full language down to this small core.

(We typically call this core language λ_s5, even though technically speaking it’s only part of what makes up λ_s5.)

These two components together give us an implementation of JavaScript: to run a program, you desugar it to λ_s5, and then run that program. And with this implementation, we can run JavaScript’s conformance test suite to check that λ_s5 is accurate: this is why it’s called a tested semantics. And lo, λ_s5 passes the relevant portion of the test262 conformance suite.

The Problem

Every blog post needs a problem, though. The problem with λ_s5 lies in desugaring. We just stated that JavaScript is complicated, while the core language for λ_s5 is simple. This means that the complications of JavaScript must be dealt with not in the core language, but instead in desugaring. Take an illustrative example. Here’s a couple of innocent lines of JavaScript:

function id(x) {
    return x;
}

These couple lines desugar into the following λ_s5 code:

{let
 (%context = %strictContext)
 { %defineGlobalVar(%context, "id");
  {let
   (#strict = true)
   {"use strict";
    {let
     (%fobj4 =
       {let
         (%prototype2 = {[#proto: %ObjectProto,
                          #class: "Object",
                          #extensible: true,]
                         'constructor' : {#value (undefined) ,
                                          #writable true ,
                                          #configurable false}})
         {let
          (%parent = %context)
          {let
           (%thisfunc3 =
             {[#proto: %FunctionProto,
               #code: func(%this , %args)
                     { %args[delete "%new"];
                       label %ret :
                       { {let
                          (%this = %resolveThis(#strict,
                                                %this))
                          {let
                           (%context =
                             {let
                               (%x1 = %args
                                        ["0" , null])
                               {[#proto: %parent,
                                 #class: "Object",
                                 #extensible: true,]
                                'arguments' : {#value (%args) ,
                                         #writable true ,
                                         #configurable false},
                                'x' : {#getter func
                                         (this , args)
                                         {label %ret :
                                         {break %ret %x1}} ,
                                       #setter func
                                         (this , args)
                                         {label %ret :
                                         {break %ret %x1 := args
                                         ["0" , {[#proto: %ArrayProto,
                                         #class: "Array",
                                         #extensible: true,]}]}}}}})
                           {break %ret %context["x" , {[#proto: null,
                                                  #class: "Object",
                                                  #extensible: true,]}];
                            undefined}}}}},
               #class: "Function",
               #extensible: true,]
              'prototype' : {#value (%prototype2) ,
                             #writable true ,
                             #configurable true},
              'length' : {#value (1.) ,
                          #writable true ,
                          #configurable true},
              'caller' : {#getter %ThrowTypeError ,
                          #setter %ThrowTypeError},
              'arguments' : {#getter %ThrowTypeError ,
                             #setter %ThrowTypeError}})
           { %prototype2["constructor" = %thisfunc3 , null];
             %thisfunc3}}}})
     %context["id" = %fobj4 ,
              {[#proto: null, #class: "Object", #extensible: true,]
               '0' : {#value (%fobj4) ,
                      #writable true ,
                      #configurable true}}]}}}}}

This is a bit much. It’s hard to read, and it’s hard for tools to process. But more to the point, λ_s5 is meant to be used by researchers, and this code bloat has stood in the way of researchers trying to adopt it. You can imagine that if you’re trying to write a tool that works over λ_s5 code, and there’s a bug in your tool and you need to debug it, and you have to wade through that much code just for the simplest of examples, it’s a bit of a nightmare.

The Ordinary Solution

So, there’s too much code. Fortunately there are well-known solutions to this problem. We implemented a number of standard compiler optimization techniques to shrink the generated λ_s5 code, while preserving its semantics. Here’s a boring list of the Semantics-Preserving optimizations we used:

Dead-code elimination
Constant folding
Constant propogation
Alias propogation
Assignment conversion
Function inlining
Infer type & eliminate static checks
Clean up unused environment bindings

Most of these are standard textbook optimizations; though the last two are specific to λ_s5. Anyhow, we did all this and got… 5-10% code shrinkage.

The Extraordinary Solution

That’s it: 5-10%.

Given the magnitude of the code bloat problem, that isn’t nearly enough shrinkage to be helpful. So let’s take a step back and ask where all this bloat came from. We would argue that code bloat can be partitioned into three categories:

Intended code bloat. Some of it is intentional. λ_s5 is a small core language, and there should be some expansion as you translate to it.
Incidental code bloat. The desugaring function from JS to λ_s5 is a simple recursive-descent function. It’s purposefully not clever, and as a result it sometimes generates redundant code. And this is exactly what the semantics-preserving rewrites we just mentioned get rid of.
Essential code bloat. Finally, some code bloat is due to the semantics of JS. JS is a complicated langauge with complicated features, and they turn into complicated λ_s5 code.

There wasn’t much to gain by way of reducing Intended or Incidental code bloat. But how do you go about reducing Essential code bloat? Well, Essential bloat is the code bloat that comes from the complications of JS. To remove it, you would simplify the language. And we did exactly that! We defined five Semantics-Altering transformations:

(IR) Identifier restoration: pretend that JS is lexically scoped
(FR) Function restoration: pretend that JS functions are just functions and not function-object-things.
(FA) Fixed arity: pretend that JS functions always take as many arguments as they’re declared with.
(UAE) Assertion elimination: unsafely remove some runtime checks (your code is correct anyways, right?)
(SAO) Simplifying arithmetic operators: eliminate strange behavior for basic operators like “+”.

These semantics-altering transformations blasphemously break the language. This is actually OK, though! The thing is, if you’re studying JS or doing static analysis, you probably already aren’t handling the whole language. It’s too complicated, so instead you handle a sub-language. And this is exactly what these semantics-altering transformations capture: they are simplifying assumptions about the JS language.

Lessons about JavaScript

And we can learn about JavaScript from them. We implemented these transformations for λ_s5, and so we could run the test suite with the transformations turned on and see how many tests broke. This gives a crude measure of “correctness”: a transformation is 50% correct if it breaks half the tests. Here’s the graph:

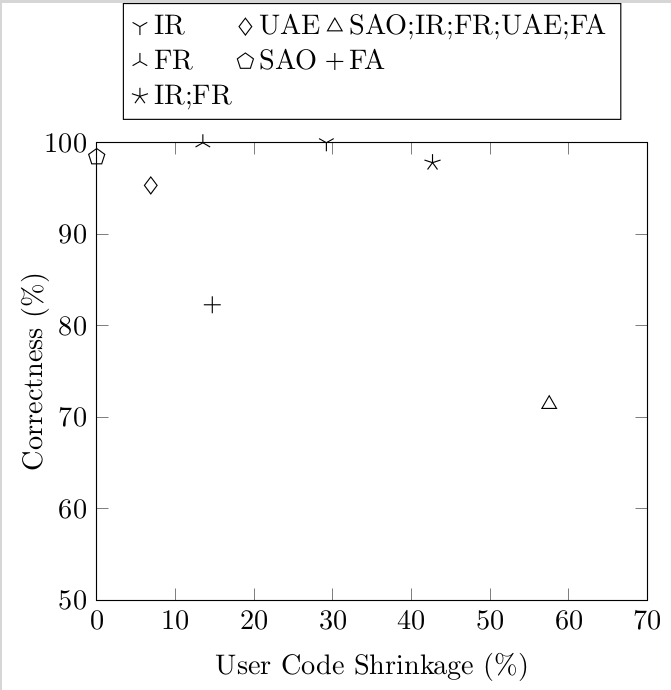
Notice that the semantics-altering transformations shrink code by more than 50%: this is way better than the 5-10% that the semantics-preserving ones gave. Going back to the three kinds of code bloat, this shows that most code bloat in λ_s5 is Essential: it comes from the complicated semantics of JS, and if you simplify the semantics you can make it go away.

Next, here’s the shrinkages of each of the semantics-altering transformations:

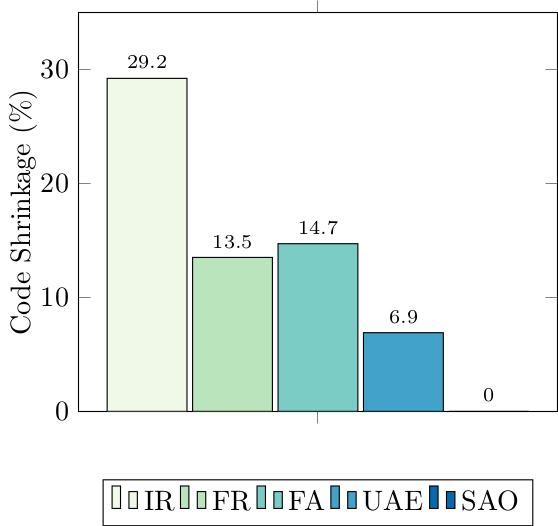
Since these semantics-altering transformations are simplifications of JS semantics, and desugared code size is a measure of complexity, you can view this graph as a (crude!) measure of complexity of language features. In this light, notice IR (Identifier Restoration): it crushes the other transformations by giving 30% code reduction. This shows that JavaScript’s scope is complex: by this metric 30% of JavaScript’s complexity is due to its scope.

Takeaway

These semantics-altering transformations give semantic restrictions on JS. Our paper makes these restrictions precise. And they’re exactly the sorts of simplifying assumptions that papers need to make to reason about JS. You can even download λ_s5 from git and implement your analysis over λ_s5 with a subset of these restrictions turned on, and test it. So let’s work toward a future where papers that talk about JS say exactly what sub-language of JS they mean.

The Paper

This is just a teaser: to read more, see the paper.

From MOOC Students to Researchers

Tags: Education, Programming Languages, Semantics

Posted on 18 June 2013.

Much has been written about MOOCs, including the potential for its users to be treated, in effect, as research subjects: with tens of thousands of users, patterns in their behavior will stand out starkly with statistical significance. Much less has been written about using MOOC participants as researchers themselves. This is the experiment we ran last fall, successfully.

Our goal was to construct a “tested semantics” for Python, a popular programming language. This requires some explanation. A semantics is a formal description of the behavior of a language so that, given any program, a user can precisely predict what the program is going to do. A “tested” semantics is one that is validated by checking it against real implementations of the language itself (such as the ones that run on your computer).

Constructing a tested semantics requires covering all of a large language, carefully translating its every detail into a small core language. Sometimes, a feature can be difficult to translate. Usually, this just requires additional quantities of patience, creativity, or elbow grease; in rare instances, it may require extending the core language. Doing this for a whole real-world language is thus a back-breaking effort.

Our group has had some success building such semantics for multiple languages and systems. In particular, our semantics for JavaScript has come to be used widely. The degree of interest and rapidity of uptake of that work made clear that there was interest in this style of semantics for other languages, too. Python, which is not only popular but also large and complex (much more so than JavaScript), therefore seemed like an obvious next target. However, whereas the first JavaScript effort (for version 3 of the language) took a few months for a PhD student and an undergrad, the second one (focusing primarily on the strict-mode of version 5) took far more effort (a post-doc, two PhD students, and a master's student). JavaScript 5 approaches, but still doesn't match, the complexity of Python. So the degree of resources we would need seemed daunting.

Crowdsourcing such an effort through, say, Mechanical Turk did not seem very feasible (though we encourage someone else to try!). Rather, we needed a trained workforce with some familiarity with the activity of formally defining a programming language. In some sense, Duolingo has a similar problem: to be able to translate documents it needs people who know languages. Duolingo addresses it by...teaching languages! In a similar vein, our MOOC on programming languages was going to serve the same purpose. The MOOC would deliver a large and talented workforce; if we could motivate them, we could then harness them to help perform the research.

During the semester, we therefore gave three assignments to get students warmed up on Python: 1, 2, and 3. By the end of these three assignments, all students in the class had had some experience wrestling with the behavior of a real (and messy) programming language, writing a definitional interpreter for its core, desugaring the language to this core, and testing this desugaring against (excerpts of) real test suites. The set of features was chosen carefully to be both representative and attainable within the time of the course.

(To be clear, we didn't assign these projects only because we were interested in building a Python semantics. We felt there would be genuine value for our students in wrestling with these assignments. In retrospect, however, this was too much work, and it interfered with other pedagogic aspects of the course. As a result, we're planning to shift this workload to a separate, half-course on implementing languages.)

Once the semester was over, we were ready for the real business to begin. Based on the final solutions, we invited several students (out of a much larger population of talent) to participate in taking the project from this toy sub-language to the whole Python language. We eventually ended up with an equal number of people who were Brown students and who were from outside Brown. The three Brown students were undergraduates; the three outsiders were an undergraduate student, a professional programmer, and a retired IT professional who now does triathlons. The three outsiders were from Argentina, China, and India. The project was overseen by a Brown CS PhD student.

Even with this talented workforce, and the prior preparation done through the course and creating the assignments prepared for the course, getting the semantics to a reasonable state was a daunting task. It is clear to us that it would have been impossible to produce an equivalent quality artifact—or to even come close—without this many people participating. As such, we feel our strategy of using the MOOC was vindicated. The resulting paper has just been accepted at a prestigious venue that was the most appropriate one for this kind of work, with eight authors: the lead PhD student, the three Brown undergrads, the three non-Brown people, and the professor.

A natural question is whether making the team even larger would have helped. As we know from Fred Brooks's classic The Mythical Man Month, adding people to projects can often hurt rather than help. Therefore, the determinant is to what extent the work can be truly parallelized. Creating a tested semantics, as we did, has a fair bit of parallelism, but we may have been reaching its limits. Other tasks that have previously been crowdsourced—such as looking for stellar phenomena or trying to fold proteins—are, as the colloquial phrase has it, “embarrassingly parallel”. Most real research problems are unlikely to have this property.

In short, the participants of a MOOC don't only need to be thought of as passive students. With the right training and motivation, they can become equal members of a distributed research group, one that might even have staying power over time. Also, participation in such a project can help a person establish their research abilities even when they are at some remove from a research center. Indeed, the foreign undergraduate in our project will be coming to Brown as a master's student in the fall!

Would we do it again? For this fall, we discussed repeating the experiment, and indeed considered ways of restructuring the course to better support this goal. But before we do, we have decided to try to use machine learning instead. Once again, machines may put people out of work.

(Sub)Typing First Class Field Names

Tags: Programming Languages, Semantics, Types

Posted on 10 December 2012.

This post picks up where a previous post left off, and jumps back into the action with subtyping.

Updating Subtyping

There are two traditional rules for subtyping records, historically known as width and depth subtyping. Width subtyping allows generalization by dropping fields; one record is a supertype of another if it contains a subset of the sub-record's fields at the same types. Depth subtyping allows generalization within a field; one record is a supertype of another if it is identical aside from generalizing one field to a supertype of the type in the same field in the sub-record.

We would like to understand both of these kinds of subtyping in the context of our first-class field names. With traditional record types, fields are either mentioned in the record or not. Thus, for each possible field in both types, there are four combinations to consider. We can describe width and depth subtyping in a table:

`T₁`	`T₂`	`T₁ <: T₂` if...
`f: S`	`f: T`	`S <: T`
`f: -`	`f: T`	Never
`f: S`	`f: -`	Always
`f: -`	`f: -`	Always

We read f: S as saying that T₁ has the field f with type S, and we read f: - as saying that the corresponding type doesn't mention the field f. The first row of the table corresponds to depth subtyping, where the field f is still present, but at a more general type in T₂. The second row is a failure to subtype, when T₂ has a field that isn't mentioned at all in T₁. The third row corresponds to width subtyping, where a field is dropped and not mentioned in the supertype. The last row is a trivial case, where neither type mentions the field.

For records with string patterns, we can extend this table with new combinations to account for ○ and ↓ annotations. The old rows remain, and become the ↓ cases, and new rows are added for ○ annotations:

`T₁`	`T₂`	`T₁ <: T₂` if...
`f^↓: S`	`f^↓: T`	`S <: T`
`f^○: S`	`f^↓: T`	Never
`f: -`	`f^↓: T`	Never
`f^↓: S`	`f^○: T`	`S <: T`
`f^○: S`	`f^○: T`	`S <: T`
`f: -`	`f^○: T`	Never
`f^↓: S`	`f: -`	Always
`f^○: S`	`f: -`	Always
`f: -`	`f: -`	Always

Here, we see that it is safe to treat a definitely present field as a possibly-present one, in the case where we compare f^↓:S to f^○:T). The dual of this case, treating a possibly-present field as definitely-present, is unsafe, as the comparison of f^○:S to f^↓:T shows. Possibly present annotations do not allow us to invent fields, as having f: - on the left-hand-side is still only permissible if the right-hand-side also doesn't mention f.

Giving Types to Values

In order to ascribe these rich types to object values, we need rules for typing basic objects, and then we need to apply these subtyping rules to generalize them. As a working example, one place where objects with field patterns come up every day in practice is in JavaScript arrays. Arrays in JavaScript hold their elements in fields named by stringified numbers. Thus, a simplified type for a JavaScript array of booleans is roughly:

BoolArrayFull: { [0-9]+^○: Bool }

That is, each field made up of a sequence of digits is possibly present, and if it is there, it has a boolean value. For simplicity, let's consider a slightly neutered version of this type, where only single digit fields are allowed:

BoolArray: { [0-9]^○: Bool }

Let's think about how we'd go about typing a value that should clearly have this type: the array [true, false]. We can think of this array literal as desugaring into an object like (indeed, this is what λJS does):

{"0": true, "1": false}

We would like to be able to state that this object is a member of the BoolArray type above. The traditional rule for record typing would ascribe a type mapping the names that are present to the types of their right hand side. Since the fields are certainly present, in our notation we can write:

{"0"^↓: Bool, "1"^↓: Bool}

This type should certainly be generalizable to BoolArray. That is, it should hold (using the rules in the table above) that:

{"0"^↓: Bool, "1"^↓: Bool} <: { [0-9]^○: Bool }

Let's see what happens when we instantiate the table for these two types:

`T₁`	`T₂`	`T₁ <: T₂` if...
`0^↓: Bool`	`0^○: Bool`	`Bool <: Bool`
`1^↓: Bool`	`1^○: Bool`	`Bool <: Bool`
`3: -`	`3^○: Bool`	Fail!
`4: -`	`4^○: Bool`	Fail!
...	...	...

(We cut off the table for 5-9, which are the same as the cases for 3 and 4). Our subtyping fails to hold for these types, which don't let us reflect the fact that the fields 3 and 4 are actually absent, and we should be allowed to consider them as possibly present at the boolean type. In fact, our straightforward rule for typing records is in fact responsible for throwing away this information! The type that it ascribed,

{"0"^↓: Bool, "1"^↓: Bool}

is actually the type of many objects, including those that happen to have fields like "banana" : 42. Traditional record typing drops fields when it doesn't care if they are present or absent, which loses information about definitive absence.

We extend our type language once more to keep track of this information. We add an explicit piece of a record type that tracks a description of the fields that are definitely absent on an object, and use this for typing object literals:

p = ○ | ↓
T = ... | { L^p : T ..., L_A: abs }

Thus, the new type for ["0": true, "1": false] would be:

{"0"^↓: Bool, "1"^↓: Bool, ("0"|"1"): abs}

Here, the overbar denotes regular-expression complement, and this type is expressing that all fields other than "0" and "1" are definitely absent.

Adding another type of field annotation requires that we again extend our table of subtyping options, so we now have a complete description with 16 cases:

`T₁`	`T₂`	`T₁ <: T₂` if...
`f^↓: S`	`f^↓: T`	`S <: T`
`f^○: S`	`f^↓: T`	Never
`f: abs`	`f^↓: T`	Never
`f: -`	`f^↓: T`	Never
`f^↓: S`	`f^○: T`	`S <: T`
`f^○: S`	`f^○: T`	`S <: T`
`f: abs`	`f^○: T`	Always
`f: -`	`f^○: T`	Never
`f^↓: S`	`f: abs`	Never
`f^○: S`	`f: abs`	Never
`f: abs`	`f: abs`	Always
`f: -`	`f: abs`	Never
`f^↓: S`	`f: -`	Always
`f^○: S`	`f: -`	Always
`f: abs`	`f: -`	Always
`f: -`	`f: -`	Always

We see that absent fields cannot be generalized to be definitely present (the abs to f^↓ case), but they can be generalized to be possibly present at any type. This is expressed in the case that compares f : abs to f^○: T, which always holds for any T. To see these rules in action, we can instantiate them for the array example we've been working with to ask a new question:

{"0"^↓: Bool, "1"^↓: Bool, ("0"|"1"): abs} <: { [0-9]^○: Bool }

And the table:

`T₁`	`T₂`	`T₁ <: T₂` if...
`0^↓: Bool`	`0^○: Bool`	`Bool <: Bool`
`1^↓: Bool`	`1^○: Bool`	`Bool <: Bool`
`3: abs`	`3^○: Bool`	OK!
`4: abs`	`4^○: Bool`	OK!
...	...	...
`9: abs`	`9^○: Bool`	OK!
`foo: abs`	`foo: -`	OK!
`bar: abs`	`bar: -`	OK!
...	...	...

There's two things that make this possible. First, it is sound to generalize the absent fields that are possibly present on the array type, because the larger type doesn't guarantee their presence either. Second, it is sound to generalize absent fields that aren't mentioned on the array type, because unmentioned fields can be present or absent with any type. The combination of these two features of our subtyping relation lets us generalize from particular array instances to the more general type for arrays.

Capturing the Whole Table

The tables above present subtyping on a field-by-field basis, and the patterns we considered at first were finite. In the last case, however, the pattern of “fields other than 0 and 1” was in fact infinite, and we cannot actually construct that infinite table to describe subtyping. The writeup and its associated proof document lay out an algorithmic version of the rules presented in the tables above, and also provides a proof of their soundness.

The writeup also discusses another interesting problem, which is the interaction between these pattern types and inheritance, where patterns on the child and parent objects may overlap in subtle ways. It goes further and discusses what happens in cases like JavaScript, where the field "__proto__" is an accessible member that has inheritance semantics. Check it all out here!

Typing First Class Field Names

Tags: Programming Languages, Semantics, Types

Posted on 03 December 2012.

In a previous post, we discussed some of the powerful features of objects in scripting languages. One feature that stood out was the use of first-class strings as member names for objects. That is, in programs like

var o = {name: "Bob", age: 22};
function lookup(f) {
  return o[f];
}
lookup("name");
lookup("age");

the name position in field lookup has been abstracted over. Presumably only a finite set of names actually works with the lookup (o appears to only have two fields, after all).

It turns out that so-called “scripting” languages aren't the only ones that compute fields for lookup. For example, even within the constraints of Java's type system, the Bean framework computes method names to call at runtime. Developers can provide information about the names of fields and methods on a Bean with a BeanInfo instance, but even if they don't provide complete information, “the rest will be obtained by automatic analysis using low-level reflection of the bean classes’ methods and applying standard design patterns.” These “standard design patterns” include, for example, concatenating the strings "get" and "set" onto field names to produce method names to invoke at runtime.

Traditional type systems for objects and records have little to say about these computed accesses. In this post, we're going to build up a description of object types that can describe these values, and explore their use. The ideas in this post are developed more fully in a writeup for the FOOL Workshop.

First-class Singleton Strings

In the JavaScript example above, we said that it's likely that the only intended lookup targets―and thus the only intended arguments to lookup―are "name" and "age". Giving a meaningful type to this function is easy if we allow singleton strings as types in their own right. That is, if our type language is:

T = s | Str | Num
  | { s : T ... } | T → T | T ∩ T

Where s stands for any singleton string, Str and Num are base types for strings and numbers, respectively, record types are a map from singleton strings s to types, arrow types are traditional pairs of types, and intersections are allowed to express a conjunction of types on the same value.

Given these definitions, we could write the type of lookup as:

lookup : ("name" → Str) ∩ ("age" → Num)

That is, if lookup is provided the string "name", it produces a string, and if it is provided the string "age", it produces a number.

In order to type-check the body of lookup, we need a type for o as well. That can be represented with the type { "name" : Str, "age" : Num }. Finally, to type-check the object lookup expression o[f], we need to compare the singleton string type of f with the fields of o. In this case, only the two strings that are already present on o are possible choices for f, so the comparison is easy and type-checking works out.

For a first cut, all we did was make the string labels on objects' fields a first-class entity in our type system, with singleton string types s. But what can we say about the Bean example, where get* and set* method invocations are computed rather than just used as first-class values?

String Pattern Types

In order to express the type of objects like Beans, we need to express field name patterns, rather than just singleton field names. For example, we might say that a Bean with Int-typed parameters has a type like:

IntBean = { ("get".+)  : → Int },
            ("set".+)  : Int → Void,
            "toString" : → Str }

Here, we are using .+ as regular expression notation for any non-empty string. We read the type above as saying that all fields that begin with get and end with any string are functions that return Int values. The same is true for "set" methods. The singleton string "toString" is also a field, and is simply a function that returns strings.

To express this type, we need to extend our type language to handle these string patterns, which we write down as regular expressions (the write-up outlines the actual limits on what kinds of patterns we can support). We extend our type language to include patterns as types, and as field names:

L = regular expressions
T = L | Str | Num
  | { L : T ... } | T → T | T ∩ T

This new specification gives us the ability to write down types like IntBean, which have field patterns that describe infinite sets of fields. Let's stop and think about what that means as a description of a runtime object. Our type for o above, { "name" : Str, "age" : Num }, says that values bound to o at runtime certainly have name and age fields at the listed types. The type for IntBean, on the other hand, seems to assert that these objects will have the fields getUp, getDown, getSerious, and infinitely more. But a runtime object can't actually have all of those fields, so a pattern indicating an infinite number of field names is describing a fundamentally different kind of value.

What an object type with an infinite pattern represents is that all the fields that match the pattern are potentially present. That is, at runtime, they may or may not be there, but if they are there, they must have the annotated type. We extend object types again to make this explicit with presence annotations, which explicitly list fields as definitely present, written ↓, or possibly present, written ○:

p = ○ | ↓
T = ... | { L^p : T ... }

In this notation, we would write:

IntBean = { ("get".+)^○  : → Int },
            ("set".+)^○  : Int → Void,
            "toString"^↓ : → Str }

Which indicates that all the fields in ("get".+) and ("set".+) are possibly present with the given arrow types, and toString is definitely present.

Subtyping

Now that we have these rich object types, it's natural to ask what kinds of subtyping relationships they have with one another. A detailed account of subtyping will come soon; in the meantime, can you guess what subtyping might look like for these types?

Update: The answer is in the next post.

S5: Engineering Eval

Tags: JavaScript, Programming Languages, Semantics

Posted on 21 October 2012.

In an earlier post, we introduced S5, our semantics for ECMAScript 5.1 (ES5). S5 is no toy, but strives to correctly model JavaScript's messy details.

One such messy detail of JavaScript is eval. The behavior of eval was updated in the ES5 specification to make its behavior less surprising and give more control to programmers. However, the old behavior was left intact for backwards compatibility. This has led to a language construct with a number of subtle behaviors. Today, we're going to explore JavaScript's eval, explain its several modes, and describe our approach to engineering an implementation of it.

Quiz Time!

We've put together a short quiz to give you a tour of the various types of eval in JavaScript. How many can you get right on the first try?

The interactive quiz requires that you have JavaScript enabled. You can still see the programs we ask about below, but the experience is a lot more fun if you can click the buttons and get feedback on your answers.

Question 1

function f(x) {

  eval("var x = 2;");
  return x;
}
f(1) === ?;

f(1) === 2
This example returns 2 because the var declaration in the eval actually refers to the same variables as the body of the function. So, the eval body overwrites the x parameter and returns the new value.

Question 2

function f(x) {

  eval("'use strict'; var x = 2;");
  return x;
}
f(1) === ?;

f(1) === 1
The 'use strict'; directive creates a new scope for variables defined inside the eval. So, the var x = 2; still evaluates, but doesn't affect the x that is the function's parameter. These first two examples show that strict mode changes the scope that eval affects. We might ask, now that we've seen these, what scope does eval see?

Question 3

function f(x) {

  eval("var x = y;");
  return x;
}
f(1) === ?;

f(1) === ReferenceError: y is not defined
OK, that was sort of a trick question. This program throws an exception saying that y is unbound. But it serves to remind us of an important JavaScript feature; if a variable isn't defined in a scope, trying to access it is an exception. Now we can ask the obvious question: can we see y if we define it outside the eval?

Question 4

function f(x) {
  var y = 2;
  eval("var x = y;");
  return x;
}
f(1) === ?;

f(1) === 2
OK, here's our real answer. The y is certainly visible inside the eval, which can both see and affect the outer scope. What if the eval is strict?

Question 5

function f(x) {
  var y = 2;
  eval("'use strict'; var x = y;");
  return x;
}
f(1) === ?;

f(1) === 1
Interestingly, we don't get an error here, so it seems like y was visible to the eval even in strict mode. However, as before the assignment doesn't escape. New topic next.

Question 6

function f(x) {
  var avel = eval;
  avel("var x = y;");
  return x;
}
f(1) === ?;

f(1) === ReferenceError: y is not defined
OK, that was a gimme. Lets add the variable declaration we need.

Question 7

function f(x) {
  var avel = eval;
  var y = 2;
  avel("var x = y;");
  return x;
}
f(1) === ?;

f(1) --> ReferenceError: y is not defined
What's going on here? We defined a variable and it isn't visible like it was before, and all we did was rename eval. Let's try a simpler example.

Question 8

function f(x) {
  var avel = eval;
  avel("var x = 2;");
  return x;
}
f(1) === ?;

f(1) === 1
OK, so somehow we aren't seeing the assignment to x either... Let's try making one more observation:

Question 9

function f(x) {
  var avel = eval;
  avel("var x = 2;");
  return x;
}
f(1);
x === ?;

x === 2
Whoa! So that eval changed the x in the global scope. This is what the specification refers to as an indirect eval; when the call to eval doesn't use a direct reference to the variable eval.

Question 10 (On the home stretch!)

function f(x) {
  "use strict";
  eval("var x = 2;");
  return x;
}
f(1) === ?;
x === ?;

f(1) === 1
Before, when we had "use strict"; inside the eval, we saw that the variable declarations did not escape. Here, the "use strict"; is outside, but we see the same thing: the value of 1 simply flows through to the return statement unaffected. Second, we know that we aren't doing the same thing as the indirect eval from the previous question, because we didn't affect the global scope.

Question 11 (last one!)

function f(x) {
  "use strict";
  var avel = eval;
  avel("var x = 2;");
  return x;
}
f(1) === ?;
x === ?;

f(1) === 1
x === 2
Unlike in the previous question, this indirect eval has the same behavior as before: it affects the global scope. The presence of a "use strict"; appears to mean something different to an indirect versus a direct eval.

Capturing all the Evals

We saw three factors that could affect the behavior of eval above:

Whether the code passed to eval was in strict mode;
Whether the code surrounding the eval was in strict mode; and
Whether the eval was direct or indirect.

Each of these is a binary choice, so there are eight potential configurations for an eval. Each of the eight cases specifies both:

Whether the eval sees the current scope or the global one;
Whether variables introduced in the eval are seen outside of it.

We can crisply describe all of these choices in a table:

Strict outside?	Strict inside?	Direct or Indirect?	Local or global scope?	Affects scope?
Yes	Yes	Indirect	Global	No
No	Yes	Indirect	Global	No
Yes	No	Indirect	Global	Yes
No	No	Indirect	Global	Yes
Yes	Yes	Direct	Local	No
No	Yes	Direct	Local	No
Yes	No	Direct	Local	No
No	No	Direct	Local	Yes

Rows where eval can affect some scope are shown in red (where it cannot is blue), and rows where the string passed to eval is strict mode code are in bold. Some patterns emerge here that make some of the design decisions of eval clear. For example:

If the eval is indirect it always uses global scope; if direct it always uses local scope.
If the string passed to eval is strict mode code, then variable declarations will not be seen outside the eval.
An indirect eval behaves the same regardless of the strictness of its context, while direct eval is sensitive to it.

Engineering `eval`

To specify eval, we need to somehow both detect these different configurations, and evaluate code with the right combination of visible environment and effects. To do so, we start with a flexible primitive that lets us evaluate code in an environment expressed as an object:

internal-eval(string, env-object)

This internal-eval expects env-object to be an object whose fields represent the environment to evaluate in. No identifiers other than those in the passed-in environment are bound. For example, a call like:

internal-eval("x + y", { "x" : 2, "y" : 5 })

Would evaluate to 7, using the values of the "x" and "y" fields from the environment object as the bindings for the identifiers x and y. With this core primitive, we have the control we need to implement all the different versions of eval.

In previous posts, we talked about the overall strategy of our evaluator for JavaScript. The relevant high-level point for this discussion is that we define a core language, dubbed S5, that contains only the essential features of JavaScript. Then, we define a source-to-source transformer, called desugar, that converts JavaScript programs to S5 programs. Since our evaluator is defined only over S5, we need to use desugar in our interpreter to perform the evaluation step. Semantically, the evaluation of internal-eval is then:

internal-eval(string, env-object) -> desugar(string)[x₁ / v₁, ...]
  for each x₁ : v₁ in env-object
  (where [x / v] indicates substitution)

It is the combination of desugar and the customizable environment argument to internal-eval that let us implement all of JavaScript's eval forms. We actually desugar all calls to JavaScript's eval into a function call defined in S5 called maybeDirectEval, which performs all the necessary checks to construct the correct environment for the eval.

Leveraging S5's Eval

With our implementation of eval, we have made progress on a few fronts.

Analyzing more JavaScript: We can now tackle more programs than any of our prior formal semantics for JavaScript. For example, we can actually run all of the complicated evals in Secure ECMAScript, and print the heap inside a use of a sandboxed eval. This enables new kinds of analyses that we haven't been able to perform before.

Understanding scripting languages' eval: Other scripting languages, like Ruby and Python, also have eval. Their implementations are closer to our internal-eval, in that they take dictionary arguments that specify the bindings that are available inside the evaluation. Is something like internal-eval, which was inspired by well-known semantic considerations, a useful underlying mechanism to use to describe all of these?

The implementation of S5 is open-source, and a detailed report of our strategy and test results is appearing at the Dynamic Languages Symposium. Check them out if you'd like to learn more!

Progressive Types

Tags: Programming Languages, Semantics, Types

Posted on 01 September 2012.

Adding types to untyped languages has been studied extensively, and with good reason. Type systems offer developers strong static guarantees about the behavior of their programs, and adding types to untyped code allows developers to reap these benefits without having to rewrite their entire code base. However, these guarantees come at a cost. Retrofitting types on to untyped code can be an onerous and time-consuming process. In order to mitigate this cost, researchers have developed methods to type partial programs or sections of programs, or to allow looser guarantees from the type system. (Gradual typing and soft typing are some examples.) This reduces the up-front cost of typing a program.

However, these approaches only address a part of the problem. Even if the programmer is willing to expend the effort to type the program, he still cannot control what counts as an acceptable program; that is determined by the type system. This significantly reduces the flexibility of the language and forces the programmer to work within a very strict framework. To demonstrate this, observe the following program in Racket...

#lang racket

(define (gt2 x y)
  (> x y))

...and its Typed Racket counterpart.

#lang typed/racket

(: gt2 (Number Number -> Boolean))
(define (gt2 x y)
  (> x y))

The typed example above, which appears to be logically typed, fails to type-check. This is due to the sophistication with which Typed Racket handles numbers. It can distinguish between complex numbers and real numbers, integers and non-integers, even positive and negative integers. In this system, Number is actually an alias for Complex. This makes sense in that complex numbers are in fact the super type of all other numbers. However, it would also be reasonable to assume that Number means Real, because that's what people tend to think of when they think “number”. Because of this, a developer may expect all functions over real numbers to work over Numbers. However, this is not the case. Greater-than, which is defined over reals, cannot be used with Number because it is not defined over complex numbers. Now, this could be resolved by changing the type of gt2 to take Reals, rather than Numbers. But then consider this program:

#lang typed/racket

(: plus (Number Number -> Number))
(define (plus x y)
  (+ x y))
;Looks fine so far...

(: gt2 (Real Real -> Boolean))
(define (gt2 x y)
  (> x y))
;...Still ok...

(gt2 (plus 3 4) 5)
;...Here (plus 3 4) evaluates to a Number which causes gt2 to give 
;the type error “Expected Real but got Complex”.

Now, in order to make this program type, we would have to adjust plus to return Reals, even though it works with it's current typing! And we'd have to do the same for every program that calls plus. This can cause a ripple effect through the program, making typing the program labor-intensive, despite the fact that the program will actually run just fine on some inputs, which may be all we care about. But we still have to jump through hoops to get the program to run at all!

In the above example, the type system in Typed Racket requires the programmer to ensure that there are no runtime errors caused by using a complex number where a real number is expected, even if it means significant extra programming effort. There are cases, however, where type systems do not provide guarantees because it would cross the threshold of too much work for programmers. One such guarantee is ensuring that vector references are always given positive integer inputs. The Typed Racket type system does not offer this guarantee because of the required programming effort, and so it traded that particular guarantee for convenience and ease of programming.

In both these cases, type systems are trying to determine the best balance betwen safety and convenience. However, the best a system can do is choose either safety or convenience and apply that to all programs. Vector references cannot be checked in any program, because it isn't worth the extra engineering effort, whereas all programs must be checked for number realness, because it's worth the extra engineering effort. This seems pretty arbirtary! Type systems are trying to guess at what the developer might want, instead of just asking. However, the developer has a much better idea of which checks are relevant and important for a specific program and which are irrelevant or unimportant. The type system should leverage this information and offer the useful guarantees without requiring unhelpful ones.

Progressive Types

To this end, we have developed progressive types, which allow the developer to require type guarantees that are significant to the program, and ignore those that are irrelevant. From the total set of possible type errors, the developer would select which among them must be detected as compile time type errors, and which should be allowed to possibly cause runtime failures. In the above example, the developer could allow errors caused by treating a Number as a Real at runtime, trusting that they will never occur or that it won't be catastrophic if they do or that the particular error is orthogonal to the reasons for type-checking the program at all. Thus, the developer can disregard an insignificant error while still reaping the benefits of the rest of the type system. This addresses a problem that underlies all type systems: The programmer doesn't get to choose which classes of programs are “good” and which are “bad.” Progressive types give the programmer that control.

In order to allow this, the type system has an allowed error set, Ω, in addition to the type environment. So while a traditional typing rule takes the form Γ⊢e:τ, a rule in progressive type would take the form Ω;Γ⊢e:τ. Here, Ω is the set of errors the developer wants to allow to cause runtime failures. Expressions may evaluate to errors, and if those errors are in Ω, the expression will type to ⊥, otherwise it will fail to type. This is reflected in the progress theorem that goes along with the type system.

If Typed Racket were a progressively typed language, the above program would type only if the programmer had selected “Expected Real, but got Complex” to be in Ω. This means that if numerical calculations are really orthogonal to the point of the program, or there are other checks in place insuring the function will only get the right type of input, the developer can just tell the type checker not to worry about those errors! However, if it's important to ensure that complex numbers never appear where reals are required, the developer can tell the type checker to detect those errors. Thus the programmer can determine what constitutes a “good” program, rather than working around a different, possibly inconvenient, definition of “good”. By passing this control over to the developer, progressive type systems allow the balance between ease of engineering and saftey to be set at a level appropriate to the program.

Progressive typing differs from gradual typing in that while gradual typing allows the developer to type portions of a program with a fixed type system, progressive types instead allow the developer to vary the guarantees offered by the type system. Further, like soft typing, progressive typing allows for runtime errors instead of static guarantees, but unlike soft typing, it restricts which classes of runtime failures are allowed to occur. Because our system allows programmers to progressively adjust the restrictions imposed by the type system, either to loosen or tighten them, they can reap many of the flexibility benefits of a dynamic languages, but get static guarantees of a type system in the way best suited to each of their programs or preferences.

If you are interested in learning more about progressive types, look here.

Modeling DOM Events

Tags: Browsers, JavaScript, Semantics

Posted on 17 July 2012.

In previous posts, we’ve talked about our group’s work on providing an operational semantics for JavaScript, including the newer features of the language. While that work is useful for understanding the language, most JavaScript programs don’t run in a vacuum: they run in a browser, with a rich API to access the contents of the page.

That API, known as the Document Object Model (or DOM), consists of several parts:

A graph of objects encoding the structure of page (This graph is optimistically called a "tree" since the HTML markup is indeed tree-shaped, but this graph has extra pointers between objects.),
Methods to manipulate the HTML tree structure,
A sophisticated event model to allow scripts to react to user interactions.

These three parts of the DOM interact with one other, making reasoning about any one of them in isolation challenging. Moreover, the specs describing them are long, heavily self-referential, and difficult to understand incrementally. So what to do?

What makes this event programming so special?

To a first approximation, the execution of every web page looks roughly like: load the markup of the page, load scripts, set up lots of event handlers … and wait. For events. To fire. Accordingly, to understand the control flow of a page, we have to understand what happens when events fire.

Let’s start with this:

  <div id="d1">
    In outer div
    <p id="p1">
      In paragraph in div.
      <span id="s1" style="background:white;">
        In span in paragraph in div.
      </span>
    </p>
  </div>
  <script>
    document.getElementById("s1").addEventListener("click",
      function() { this.style.color = "red"; });
  </script>

Requires JavaScript enabled to view the example

If you click on the text "In span in paragraph in div" the event listener that gets added to element span#s1 is triggered by the click, and turns the text red. But consider the slightly more complicated example:

  <div id="d2">
    In outer div
    <p id="p2">
      In paragraph in div.
      <span id="s2" style="background:white;">
        In span in paragraph in div.
      </span>
    </p>
  </div>
  <script>
    document.getElementById("d2").addEventListener("click",
      function() { this.style.color = "red"; });
    document.getElementById("s2").addEventListener("click",
      function() { this.style.color = "blue"; });
  </script>

Requires JavaScript enabled to view the example

Now, clicking anywhere in the box will turn all the text red. That makes sense: we just clicked on the <div> element, so its listener fires. But clicking on the <span> will turn it blue and still turn the rest red. Why? We didn’t click on the <div>! Well, not directly…

The key feature of event dispatch, as implemented for the DOM, is that it takes advantage of the page structure. Clicking on an element of the page (or typing into a text box, moving the mouse over an element, etc.) will cause an event to fire "at" that element: the element is the target of the event, and any event listener installed for that event on that target node will be called. But in addition, the event will also trigger event listeners on the ancestors of the target node: this is called the dispatch path. So in the example above, because div#d2 is an ancestor of span#s2, its event listener is also invoked, turning the text red.

What Could Possibly Go Wrong?

In a word: mutation. The functions called as event listeners are arbitrary JavaScript code, which can do anything they want to the state of the page, including modifying the DOM. So what might happen?

The event listener might move the current target in the page. What happens to the dispatch path?
The event listener adds (or removes) other listeners for the event being dispatched. Should newly installed listeners be invoked before or after existing ones? Should those listeners even be called?
The event listener tries to cancel event dispatch. Can it do so?
The listener tries to (programmatically) fire another event while the current one is active. Is event dispatch reentrant?
There are legacy mechanisms to add event "handlers" as well as listeners. How should they interact with listeners?

Modeling Event Dispatch

Continuing our group’s theme of reducing a complicated, real-world system to a simpler operational model, we developed an idealized version of event dispatch in PLT Redex, a domain-specific language embedded in Racket for specifying operational semantics. Because we are focusing on exactly how event dispatch works, our model does not include all of JavaScript, nor does it need to—instead, it includes a miniature statement language containing the handful of DOM APIs that manipulate events. Our model does not include all the thousands of DOM properties and methods, instead including just a simplified tree-structured heap of nodes: this is all the structure we need to faithfully model the dispatch path of an event.

Our model is based on the DOM Level 3 Events specification. It expresses the key behaviors of event dispatch, and does so far more compactly than the spec: roughly 1000 lines of commented Redex code replace several pages’ worth of (at times self-contradictory!) requirements that are spread throughout a spec over a hundred pages long. From this concise model, for example, we can easily extract a state machine describing the key stages of dispatch:

From this state machine, it’s much easier to answer the questions raised above, precisely and formally. For example, if an event listener moves the event target in the page, nothing happens to the dispatch path: only the first state of the machine constructs the dispatch path, while all the others just read from it. Done! It’s unfortunate that this state machine isn't sketched in the spec anywhere…

Moreover, the model is executable: Redex allows us to construct test cases—randomly, systematically, or ad-hoc, as we choose—and then run them through our model and see what output it produces. Even better, we can export our tests to HTML and JavaScript, and run them in real browsers and compare results:

Comparing a test model (tree structure, event listeners, and an event to be fired) in our semantics, and in various browsers.

Most importantly, our model agrees with all browsers on most test cases: this gives us confidence that our model is faithful to the intent of the spec. But not all test cases—not too surprisingly, we identified examples where real-world browsers differ in their behavior. Under our reading of the spec, at least one of these browsers is wrong—but since the spec is so intricate, it is easy to see why browsers have a hard time agreeing in all cases!

What’s Done

Here’s what we’ve got so far:

What’s Next

Since our original JavaScript semantics was also written in Redex, we can combine our model of event dispatch with the JavaScript one, for a much higher-fidelity model of what event listeners can do in a browser setting. Then of course there are further applications, such as building a precise control-flow analysis of web pages and analyzing their code. And other uses? If you’re interested in using our model, let us know!

Mechanized LambdaJS

Tags: JavaScript, Programming Languages, Semantics

Posted on 04 June 2012.

See the discussion on Lambda the Ultimate about this work.

In an earlier post, we introduced λ_JS, our operational semantics for JavaScript. Unlike many other operational semantics, λ_JS is no toy, but strives to correctly model JavaScript's messy details. To validate these claims, we test λ_JS with randomly generated tests and with portions of the Mozilla JavaScript test suite.

Testing is not enough. Despite our work, other researchers found a missing case in λ_JS. Today, we're introducing Mechanized λ_JS, which comes with a machine-checked proof of correctness, using the Coq proof assistant.

Recap: The Structure of λ_JS

λ_JS has two key parts: an operational semantics and a desugaring function. Our earlier post discusses how we tackle the minutiae of JavaScript with our desugaring function. This post focuses on the operational semantics, where others found a bug, which now has a machine-checked proof of correctness.

The operational semantics is typical of programming languages research. It specifies the sequence of steps required to evaluate the program. For example, the following sequence evaluates to a value:

  { x: 2 + 3, y : 9 }["x"] * (11 + 23)
→ { x: 5, y: 9 }["x"] * (11 + 23)
→ 5 * (11 + 23)
→ 5 * 34
→ 170

The sequence above evaluates expressions from left to right—a detail spelled out in the operational semantics.

Not all expressions reduce to values. For example, the following reduces to an error:

  null["x"]
→ err "Cannot read property 'x' of null"

An operational semantics specifies exactly which errors may occur.

Finally, an operational semantics allows some programs to run forever. This is a basic infinite loop, and its non-terminating reduction sequence:

  while (true) { 1; }
→ if true then 1; while (true) { 1; } else undefined
→ 1; while (true) { 1; }
→ while (true) { 1; }
→ if true then 1; while (true) { 1; } else undefined
→ 1; while (true) { 1; }
…

In general, these are the only three cases that the semantics should allow—an expression must either (1) evaluate to a value, (2) signal an error, or (3) not terminate. In fact, we can state that as a theorem.

Theorem 1 (Soundness). For all λ_JS programs, p, either:

p →* v,
p →* err, or
p →* p₂, and there exists a p₃ such that p₂ → p₃.

This is a standard theorem worth proving for any language. Since languages and their correctness proofs involve detailed, delicate designs and decisions, the proofs are easy to do wrong, and tedious for humans to get right. If only computers could help.

PLT Redex: Lightweight Mechanization

We first developed λ_JS in PLT Redex, a domain-specific language embedded in Racket for specifying operational semantics.

Redex brings dull semantics to life. It doesn't just make a semantics executable, but also lets you visualize it. For example, here is our first example sequence in Redex (parentheses included):

The visualizer is a lot of fun, and a very effective debugging tool. It helped us catch several bugs in the early design of λ_JS.

Redex can also generate random tests to exercise your semantics. Random testing caught several more bugs in λ_JS.

Coq: A Machine-Checked Proof

Testing is not enough. We shipped λ_JS with a bug that breaks the soundness theorem above. We didn't discover it for a year. David van Horn and Ian Zerny both reported it to us independently. We'd missed a case in the semantics, which caused certain terms to get "stuck". It turned out to be a simple fix, but we were left wondering if anything else was left lurking.

To gain further assurance, we mechanized λ_JS with the Coq proof assistant. The soundness theorem now has a machine-checked proof of correctness. You still need to read the Coq definition of λ_JS and ensure it matches your intuitions. But once that's done, you can be confident that the proofs are valid.

Doing this proof was surprisingly easy, once we'd read Software Foundations and Certified Programming with Dependent Types. We'd like to thank Benjamin Pierce and his co-authors, and Adam Chlipala, for putting their books online.

What's Done

Here's what we've got so far:

What's Next

We're not done. Here's what's coming up:

There are a few easy bits missing from the Coq model (e.g., a parameterized delta-function).
Once those easy bits are done, we'll wire it together with desugaring.
Finally, we'll upgrade the model to support semantics for ECMAScript 5.

Objects in Scripting Languages

Tags: JavaScript, Programming Languages, Semantics

Posted on 28 February 2012.

We've been studying scripting languages in some detail, and have collected a number features of their object systems that we find unusually expressive. This expressiveness can be quite powerful, but also challenges attempts to reason about and understand programs that use these features. This post outlines some of these exceptionally expressive features for those who may not be intimately familiar with them.

Dictionaries with Inheritance

Untyped scripting languages implement objects as dictionaries mapping member names (strings) to values. Inheritance affects member lookup, but does not affect updates and deletion. This won't suprise any experienced JavaScript programmer:

var parent = {"z": 9};
// Using __proto__ sets up inheritance directly in most browsers
var obj = { "x": 1, "__proto__": parent};

obj.x       // evaluates to 1
obj.z       // evaluates to 9
obj.z = 50  // creates new field on obj
obj.z       // evaluates to 50, z on parent is "overridden"
parent.z    // evaluates to 9; parent.z was unaffected by obj.z = 50

In other scripting languages, setting up this inheritance can't be done quite so directly. Still, its effect can be accomplished, and the similar object structure observed. For example, in Python:

class parent(object):
  z = 9                 # class member
  def __init__(self):
    self.x = 1          # instance member

obj = parent()

obj.x                 # evaluates to 1
obj.z                 # evaluates to 9
obj.z = 50            # creates new field on obj
obj.z                 # evaluates to 50, z on parent is "overridden"
parent.z              # evaluates to 9, just like JavaScript

We can delete the field in both languages, which returns obj to its original state, before it was extended with a z member. In JavaScript:

delete obj.z;
obj.z               // evaluates to 9 again

This also works in Python:

delattr(obj, "z");
obj.z               # evaluates to 9 again

In both languages, we could have performed the assignments and lookups with computed strings as well:

// JavaScript
obj["x " + "yz"] = 99         // creates a new field, "x yz"
obj["x y" + "z"]              // evaluates to 99

# Python
setattr(obj, "x " + "yz", 99) # creates a new field, "x yz"
getattr(obj, "x y" + "z")     # evaluates to 99

We can go through this entire progression in Ruby, as well:

class Parent; def z; return 9; end; end
obj = Parent.new
class << obj; def x; return 1; end; end

obj.x # returns 1
obj.z # returns 9
class << obj; def z; return 50; end; end
obj.z # return 50

# no simple way to invoke shadowed z method
class << obj; remove_method :z; end
obj.z # returns 9

class << obj
  define_method("xyz".to_sym) do; return 99; end
end
print obj.xyz # returns 99

Classes Do Not Shape Objects

The upshot is that a class definition in a scripting language says little about the structure of its instances. This is in contrast to a language like Java, in which objects' structure is completely determined by their class, to the point where memory layouts can be predetermined for runtime objects. In scripting languages, this isn't the case. An object is an instance of a 'class' in JavaScript, Python, or Ruby merely by virtue of several references to other runtime objects. Some of these be changed at runtime, others cannot, but in all cases, members can be added to and removed from the inheriting objects. This flexibility can lead to some unusual situations.

Brittle inheritance: Fluid classes make inheritance brittle. If we start with this Ruby class:

class A
  def initialize; @privateFld = 90; end

  def myMethod; return @privateFld * @privateFld; end
end

Then we might assume that implementation of myMethod assumes a numeric type for @privateFld. This assumption can be broken by subclasses, however:

class B < A
  def initialize; super(); @privateFld = "string (not num)"; end
end

Since both A and B use the same name, and it is simply a dictionary key, B instances violate the assumptions of A's methods:

obj = B.new
B.myMethod   # error: cannot multiply strings

Ruby's authors are well aware of this; the Ruby manual states "it is only safe to extend Ruby classes when you are familiar with (and in control of) the implementation of the superclass" (page 240).

Mutable Inheritance: JavaScript and Python expose the inheritance chain through mutable object members. In JavaScript, we already saw that the member "__proto__" could be used to implement inheritance directly. The "__proto__" member is mutable, so class hierarchies can be changed at runtime. We found it a bit more surprising when we realized the same was possible in Python:

class A(object):
  def method(self): return "from class A"

class B(object):
  def method(self): return "from class B"

obj = A()
obj.method()       # evaluates to "from class A"
isinstance(obj, A) # evaluates to True

obj.__class__ = B  # the __class__ member determines inheritance
obj.method()       # evaluates to "from class B"
isinstance(obj, B) # evaluates to True: obj's 'class' has changed!

Methods?

These scripting languages also have flexible, and different, definitions of "methods".

JavaScript simply does not have methods. The syntax

obj.method(...)

Binds this to the value of obj in the body of method. However, the method member is just a function and can be easily extracted and applied:

var f = obj.method; f(...);

Since f() does not use the method call syntax above, it is treated as a function call. In this case, it is a well known JavaScript wart that this is bound to a default "global object" rather than obj.

Python and Ruby make a greater effort to retain a binding for the this parameter. Python doesn't care about the name of the parameter (though self is canonically used), and simply has special semantics for the first argument of a method. If a method is extracted via member access, it returns a function that binds the object from the member access to the first parameter:

class A(object):
  def __init__(self_in_init): self_in_init.myField = 900
  def method(self_in_method): return self_in_method.myField

obj = A()
f1 = obj.method  # the access binds self_in_method to obj
f1()             # evaluates to 900, using the above binding

If the same method is accessed as a field multiple times, it isn't the same function both times―a new function is created for each access:

obj = A()
f1 = obj.method  # first extraction
f2 = obj.method  # second extraction

f1 is f2         # evaluates to False, no reference equality

Python lets programmers access the underlying function without the first parameter bound through the member im_func. This is actually the same reference across all extracted methods, regardless of even the original object of extraction:

obj = A()
f1 = obj.method  # first extraction
f2 = obj.method  # second extraction

otherobj = A()
f3 = obj.method  # extraction from another object

# evaluates to True, same function referenced from extractions on the
# same object
f1.im_func is f2.im_func

# evaluates to True, same function referenced from extractions on
# different objects
f2.im_func is f3.im_func

Ruby has a similar treatment of methods, their extraction, and their reapplication to new arguments.

But Why?

These features aren't just curiosities―we've found examples where they are used in practice. For example, Django's ORM builds classes dynamically, modifying them based on strings that come from modules describing database tables and relationships ( base.py):

attr_name = '%s_ptr' % base._meta.module_name
field = OneToOneField(base, name=attr_name,
        auto_created=True, parent_link=True)
new_class.add_to_class(attr_name, field)

Ruby on Rails' ActiveRecord uses dynamic field names as well, iterating over fields and invoking methods only when their names match certain patterns ( base.rb):

attributes.each do |k, v|
  if k.include?("(")
    multi_parameter_attributes << [ k, v]
  elsif respond_to?("#{k}=")
    if v.is_a?(Hash)
      nested_parameter_attributes << [ k, v ]
    else
    send("#{k}=", v)
  else
    raise(UnkownAttributeError, "unknown attribute: #{k}")
  end
end

These applications use objects as dictionaries (with inheritance) to build up APIs that they couldn't otherwise.

These expressive features aren't without their perils. Django has explicit warnings that things can go awry if relationships between tables expressed in ORM classes overlap. And the fact that __proto__ is in the same namespace as the other members bit Google Docs, whose editor would crash if the string "__proto__" was entered. The implementation was using an object as a hashtable keyed by strings from the document, which led to an assignment to __proto__ that changed the behavior of the map.

So?

The languages presented here are widely adopted and used, and run critical systems. Yet, they contain features that defy conventional formal reasoning, at the very least in their object systems. Perhaps these features' expressiveness outweighs the cognitive load of using them. If it doesn't, and using these features is too difficult or error-prone, we should build tools to help us use them, or find better ways to implement the same functionality. And if not, we should take notice and recall that we have these powerful techniques at our disposal in the next object system we design.

S5: Wat?

Tags: JavaScript, Programming Languages, Semantics

Posted on 31 January 2012.

Gary Bernhardt's Wat talk has been making a well-deserved round of the blogodome in the past few weeks. If you haven't seen it, go give it a watch (you can count it as work time, since you saw it on the Brown PLT Blog, and we're Serious Researchers). The upshot of the second half of the talk is that JavaScript has some less than expected behaviors. We happen to have a JavaScript implementation floating around in the form of S5, and like to claim that it handles the hairy corners of the language. We decided to throw Gary's examples at it.

The Innocuous +

Gary's first JavaScript example went like this:

failbowl:~(master!?) $ jsc
> [] + []

> [] + {}
[object Object]
> {} + []
0
> {} + {}
NaN

S5 lacks a true REPL―it simply takes JavaScript strings and produces output and answers―so we started by approximating a little bit. We first tried a series of print statements to see if we got the same effect:

$ cat unit-tests/wat-arrays.js 
print([] + []);
print([] + {});
print({} + []);
print({} + {});

$ ./s5 < unit-tests/wat-arrays.js 

[object Object]
[object Object]
[object Object][object Object]
undefined

WAT.

Well, that doesn't seem good at all. Only half of the answers are right, and there's an undefined at the end. What went wrong? It turns out the semantics of REPLs are to blame. If we take the four programs and run them on their own, we get something that looks quite a bit better:

$ ./s5 "[] + []"
""

$ ./s5 "[] + {}"
"[object Object]"

$ ./s5 "{} + []"
0.

$ ./s5 "{} + {}"
nan

There are two issues here:

Why do 0. and nan print like that?
Why did this work, when the previous attempt didn't?

The answer to the first question is pretty straightforward: under the covers, S5 is using Ocaml floats and printing Ocaml values at the end of its computation, and Ocaml makes slightly different decisions than JavaScript in printing numbers. We could change S5 to print answers in JavaScript-printing mode, but the values themselves are the right ones.

The second question is more interesting. Why do we get such different answers depending on whether we evaluate individual strings versus printing the expressions? The answer is in the semantics of JavaScript REPLs. When parsing a piece of JavaScript, the REPL needs to make a choice. Sensible decisions would be to treat each new JavaScript string as a Statement, or as an entire JavaScript Program. Most REPLs choose the Program production.

The upshot is that the parsing of {} + {} is quite different from [] + []. With S5, it's trivial to print the desugared representation and understand the difference. When we parse and desugar, we get very different results for {} + {} and [] + []:

$ ./s5-print "{} + {}"
{undefined;
 %UnaryPlus({[#proto: %ObjectProto,
              #class: "Object",
              #extensible: true,]
             })}

$ ./s5-print "[] + []"
%PrimAdd({
    [#proto: %ArrayProto,
     #class: "Array",
     #extensible: true,]
    'length' : {#value 0., #writable true, #configurable false}
  },
  {
    [#proto: %ArrayProto,
     #class: "Array",
     #extensible: true,]
    'length' : {#value 0., #writable true, #configurable false}
  }
)

It is clear that {} + {} parses as two statements (an undefined followed by a UnaryPlus), and [] + [] as a single statement containing a binary addition expression. What's happening is that in the Program production, for the string {} + {}, the first {} is matched with the Block syntactic form, with no internal statements. The rest of the expression is parsed as a UnaryExpression. This is in contrast to [] + [], which only correctly parses as an ExpressionStatement containing an AdditiveExpression.

In the example where we used successive print statements, every expression in the argument position to print was parsed in the second way, hence the different answers. The lesson? When you're at a REPL, be it Firebug, Chrome, or the command line, make sure the expression you're typing is what you think it is: not being aware of this difference can make it even more difficult to know what to expect!

If You Can't Beat 'Em...

Our first example led us on an interesting excursion into parsing, from which S5 emerged triumphant, correctly modelling the richness and/or weirdness of the addition examples. Next up, Gary showed some straightforward uses of Array.join():

failbowl:~(master!?) $ jsc
> Array(16)
,,,,,,,,,,,,,,,,
> Array(16).join("wat")
watwatwatwatwatwatwatwatwatwatwatwatwatwatwatwat
> Array(16).join("wat" + 1)
wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1
> Array(16).join("wat" - 1) + " Batman"
NaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaN Batman

Our results look oh-so-promising, right up until the last line (note: we call String on the first case, because S5 doesn't automatically toString answers, which the REPL does).

$ ./s5 "String(Array(16))"
",,,,,,,,,,,,,,,,"
$ ./s5 "Array(16).join('wat')"
"watwatwatwatwatwatwatwatwatwatwatwatwatwatwatwat"
$ ./s5 "Array(16).join('wat' + 1)"
"wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1"
$ ./s5 "Array(16).join('wat' - 1) + ' Batman'"
"nullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnull Batman"

WAT.

Are we really that awful that we somehow yield null rather than NaN? A quick glance at the desugared code shows us that we actually have the constant value null as the argument to join(). How did that happen? Interestingly, the following version of the program works:

$ ./s5 "var wat = 'wat'; Array(16).join(wat - 1) + ' Batman';"
"NaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaN Batman"

This leads us to our answer. We use SpiderMonkey's very handy Parser API as part of our toolchain. Reflect.parse() takes strings and converts them to JSON structures with rich AST information, which we stringify and pass off to the innards of S5 to do desugaring and evaluation. Reflect.parse() is part of a JavaScript implementation that strives for performance, and to that end it performs constant folding. That is, as an optimization, when it sees the expression "wat" - 1, it automatically converts it to NaN. All good so far.

The issue is that the NaN yielded by constant folding is not quite the same NaN we might expect in JavaScript programs. In JavaScript, the identifier NaN is a property of the global object with the value NaN. The Parser API can't safely fold to the identifier NaN (as was pointed out to us when we reported this bug), because it might be shadowed in a different context. Presumably to avoid this pitfall, the folding yields a JSON structure that looks like:

expression:{type:"Literal", value:NaN}

But we can't sensibly use JSON.stringify() on this structure, because NaN isn't valid JSON! Any guesses on what SpiderMonkey's JSON implementation turns NaN into? If you guessed null, we owe you a cookie.

We have designed a hack based on suggestions from the bug report to get around this (passing a function to stringify to look for NaNs and return a stylized object literal instead). There's a bug open to make constant folding optional in Reflect.parse(), so this will be fixed in Mozilla's parser. (Update) The bug is fixed, and we've updated our version of Spidermonkey. This example now works happily, thanks to Dave Herman.

Producing a working JavaScript implementation leads to a whole host of exciting moments and surprising discoveries. Building this semantics and its desugaring gives us much more confidence that our tools say something meaningful about real JavaScript programs. These examples show that getting perfect correspondence is difficult, but we strive to be as close as possible.

S5: Semantics for Accessors

Tags: JavaScript, Programming Languages, Semantics

Posted on 11 December 2011.

Getters and setters (known as accessors) are a new feature in ECMAScript 5 that extend the behavior of assignment and lookup expressions on JavaScript objects. If a field has a getter defined on it, rather than simply returning the value in field lookup, a getter function is invoked, and its return value is the result of the lookup:

var timesGotten = 0;
var o = {get x() { timesGotten++; return 22; }};
o.x;         // calls the function above, evaluates to 22
timesGotten; // is now 1, due to the increment in the getter
o.x;         // calls the function above, still evaluates to 22
timesGotten; // is now 2, due to another increment in the getter

Similarly, if a field has a setter defined on it, the setter function is called on field update. The setter function gets the assigned value as its only argument, and its return value is ignored:

var foo = 0;
var o = {set x(v) { foo = v; }};
o.x = 37; // calls the function above (with v=37)
foo;      // evaluates to 37
o.x;      // evaluates to undefined

Getters and setters have a number of proposed uses―they can be used to wrap DOM objects that have interesting effects on assignment, like onmessage and onbeforeunload, for example. We leave discovering good uses to more creative JavaScript programmers, and focus on their semantic properties here.

The examples above are straightforward, and it seems like a simple model might work out quite easily. First, we need some definitions, so we'll start with what's in λ_JS. Here's a fragment of the values that λ_JS works with, and the most basic of the operations on objects:

v := str  | { str₁:v₁, ⋯, str_n:v_n } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | e(e, ⋯) | ⋯

(E-Lookup)
  { ⋯, str:v, ⋯ }[str_x] → v
  when str_x = str

(E-Update)
  { ⋯, str:v, ⋯}[str_x=v'] → { ⋯, str:v', ⋯}
  when str_x = str

(E-UpdateAdd)
  { str₁:v₁, ⋯}[str=v] → { str:v, str₁:v₁, ⋯}
  when str ≠ str₁, ⋯

We update and set fields when they are found, and add fields if there is an update on a not-found field. Clearly, this isn't enough to model the semantics of getters and setters. On lookup, if the value of a field is a getter, we need to have our semantics step to an invocation of the function. We need to make the notion of a field richer, so the semantics can have behavior that depends on the kind of field. We distinguish two kinds of fields p, one for simple values and one for accessors:

p := [get: v_g, set: v_s] | [value: v]
v := str  | { str₁:p₁, ⋯, str_n:p_n } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | e(e, ⋯) | ⋯

The updated rules for simple values are trivial to write down (differences in bold):

(E-Lookup)
  { ⋯, str:[value:v], ⋯ }[str_x] → v
  when str_x = str

(E-Update)
  { ⋯, str:[value:v], ⋯}[str_x=v'] → { ⋯, str:[value:v'], ⋯}
  when str_x = str

(E-UpdateAdd)
  { str₁:v₁, ⋯}[str=v] → { str:[value:v], str₁:v₁, ⋯}
  when str ≠ str₁, ⋯

But now we can also handle the cases where we have a getter or setter. If a lookup expression e[e] finds a getter, it applies the function, and the same goes for setters, which get the value as an argument:

(E-LookupGetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯ }[str_x] → v_g()
  when str_x = str

(E-UpdateSetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯}[str_x=v'] → v_s(v')
  when str_x = str

Great! This can handle the two examples from the beginning of the post. But those two examples weren't the whole story for getters and setters, and our first fragment wasn't the whole story for λ_JS objects.

Consider this program:

var o = {
  get x() { return this._x + 1; },
  set x(v) { this._x = v * 2; }
};
o.x = 5; // calls the set function above (with v=5)
o._x;    // evaluates to 10, because of assignment in the setter
o.x;     // evaluates to 11, because of addition in the getter

Here, we see that the functions also have access to the target object of the assignment or lookup, via the this parameter. We could try to encode this into our rules, but let's not get too far ahead of ourselves. JavaScript objects have more subtleties up their sleeves. We can't forget about prototype inheritance. Let's start with the same object o, this time called parent, and use it as the prototype of another object:

var parent = {
  get x() { return this._x + 1; },
  set x(v) { this._x = v * 2; }
};
var child = Object.create(parent);
child.x = 5; // Sets... what exactly to 10?
parent._x;   // ??? 
child._x;    // ??? 
parent.x;    // ??? 
child.x;     // ???

Take a minute to guess what you think each of the values should be. Click here to see the answers (which hopefully are what you expected).

So, JavaScript is passing the object in the lookup expression into the function, for both field access and field update. Something else subtle is going on, as well. Recall that before, when an update occurred on a field that wasn't present, JavaScript simply added it to the object. Now, on field update, we see that the assignment traverses the prototype chain to check for setters. This is fundamentally different from JavaScript before accessors―assignment never considered prototypes. So, our semantics needs to do two things:

Pass the correct this argument to getters and setters;
Traverse the prototype chain for assignments.

Let's think about a simple way to pass the this argument to getters:

(E-LookupGetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯ }[str_x] → v_g({ ⋯, str:[get:v_g, set:v_s], ⋯ })
  when str_x = str

Here, we simply copy the object over into the first argument to the function v_g. We can (and do) desugar functions to have an implicit first this argument to line up with this invocation. But we need to think carefully about this rule's interaction with prototype inheritance.

Here is E-Lookup-Proto from the original λ_JS:

(E-Lookup-Proto)
  { str₁:v₁, ⋯, "__proto__": v_p, str_n:v_n, ⋯}[str] → v_p[str]
  when str ≠ str₁, ⋯, str_n, ⋯

Let's take a moment to look at this rule in conjunction with E-LookupGetter. If the field isn't found, and __proto__ is present, it looks up the __proto__ field and performs the same lookup on that object (we are eliding the case where proto is not present or not an object for this presentation). But note something crucial: the expression on the right hand side drops everything about the original object except its prototype. If we applied this rule to child above, the getter rule would pass parent to the getter instead of child!

The solution is to keep track of the original object as we traverse the prototype chain. If we don't, the reduction relation simply won't have the information it needs to pass in to the getter or setter when it reaches the right point in the chain. This is a deep change―we need to modify our expressions to get it right:

p := [get: v_g, set: v_s] | [value: v]
v := str  | { str₁:p₁, ⋯, str_n:p_n } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | e^v[e] | e^v[e=e] | e(e, ⋯) | ⋯

And now, when we do a prototype lookup, we can keep track of the same this argument (written as v_t) the whole way up the chain, and the rules for getters and setters can use this new piece of the expression:

(E-Lookup-Proto)
  { str₁:v₁, ⋯, "__proto__": v_p, str_n:v_n, ⋯}^v_t[str] → v_p^v_t[str]
  when str ≠ str₁, ⋯, str_n, ⋯

(E-LookupGetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯ }^v_t[str_x] → v_g(v_t)
  when str_x = str

(E-UpdateSetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯}^v_t[str_x=v'] → v_s(v_t,v')
  when str_x = str

This idea was inspired by Di Gianantonio, Honsell, and Liquori's 1998 paper, A lambda calculus of objects with self-inflicted extension. They use a similar encoding to model method dispatches in a small prototype-based object calculus. The original expressions, e[e] and e[e=e], simply copy values into the new positions once the subexpressions have reduced to values:

(E-Lookup)
  v[str] → v^v[str]

(E-Update)
  v[str=v'] → v^v[str=v']

The final set of evaluation rules and expressions is a little larger:

p := [get: v_g, set: v_s] | [value: v]
v := str  | { str₁:p₁, ⋯, str_n:p_n } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | e^v[e] | e^v[e=e] | e(e, ⋯) | ⋯

(E-Lookup)
  v[str] → v^v[str]

(E-Update)
  v[str=v'] → v^v[str=v']

(E-LookupGetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯ }^v_t[str_x] → v_g(v_t)
  when str_x = str

(E-Lookup-Proto)
  { str₁:v₁, ⋯, "__proto__": v_p, str_n:v_n, ⋯}^v_t[str] → v_p^v_t[str]
  when str ≠ str₁, ⋯, str_n, ⋯

(E-UpdateSetter)
  { ⋯, str:[get:v_g, set:v_s], ⋯}^v_t[str_x=v'] → v_s(v_t,v')
  when str_x = str

(E-Update-Proto)
  { str₁:v₁, ⋯, "__proto__": v_p, str_n:v_n, ⋯}^v_t[str=v'] → v_p^v_t[str=v']
  when str ≠ str₁, ⋯, str_n, ⋯

This is most of the rules―we've elided some details to only present the key insight behind the new ones. Our full semantics (discussed in our last post), handles the details of the arguments object that is implicitly available within getters and setters, and using built-ins, like defineProperty, to add already-defined functions to existing objects as getters and setters.

S5: A Semantics for Today's JavaScript

Tags: JavaScript, Semantics, Programming Languages

Posted on 11 November 2011.

The JavaScript language isn't static―the ECMAScript committee is working hard to improve the language, and browsers are implementing features both in and outside the spec, making it difficult to understand just what "JavaScript" means at any point in time. Existing implementations aren't much help―their goal is to serve pages well and fast. We need a JavaScript architecture that can help us make sense of the upcoming (and existing!) features of the language.

To this end, we've developed S5, an ECMAScript 5 runtime, built on λ_JS, with the explicit goal of helping people understand and tinker with the language. We built it to understand the features in the new standard, building on our previous efforts for the older standard. We've now begun building analyses for this semantics, and are learning more about it as we do so. We're making it available with the hope that you can join us in playing with ES5, extending it with new features, and building tools for it.

S5 implements the core features of ES5 strict mode. How do we know this? We've tested S5 against Test262 to measure our progress. We are, of course, not feature complete, but we're happy with our progress, which you can check out here.

A Malleable Implementation

The semantics of S5 is designed to be two things: a language for writing down the algorithms of the specification, and a translation target for JavaScript programs. We've implemented an interpreter for S5, and a desugaring function that translates JavaScript source into S5 programs.

We have a number of choices to make in defining desugaring. The ECMAScript standard defines a whole host of auxiliary functions and library routines that we must model. Putting these implementations directly in the desugaring function would work, but would make desugaring unnecessary brittle, and require recompilation on every minor change. Instead, we implement the bulk of this functionality as an S5 program. The majority of our work happens in an environment file that defines the spec in S5 itself. The desugaring defines a translation from the syntactic forms of JavaScript to the (smaller) language of S5, filled with calls into the functions defined in this environment.

This separation of concerns is what makes our implementation so amenable to exploration. If you want to try something out, you can edit the environment file and rerun whatever tests you care to learn about. Want to try a different implementation of the == operator? Just change the definition, as it was pulled from the spec, at line 300. Want a more expressive Object.toString() that doesn't just print "[object Object]"? That's right here. No changing an interpreter, no recompiling a desugaring function necessary.

The environment we've written reflects the standard's algorithms as we understand them in terms of S5. The desugaring from JavaScript to S5 code with calls into this library is informed by the specification's definitions of expression and statement evaluation. We have confidence in the combination of desugaring and library implementation, given our increasing test coverage. Further, we know how to continue―implement more of the spec and pass more test cases!

More than λ_JS

S5 is built on λ_JS, but extends it in three significant ways:

Explicit getters and setters;
Object fields with attributes, like writable and configurable, built-in;
Support for eval().

For those that haven't fiddled with getters and setters, they are a new feature introduced in ECMAScript 5 that allow programmer-defined behavior on property access and assignment. Getters and setters fundamentally change how property access and assignment work. They make property assignment interact with the prototype chain, which used to not be the case, and cause syntactically similar expressions to behave quite differently at runtime. In a separate post we'll discuss the interesting problems they introduce for desugaring and how we implement them in the semantics. (Update: This post has been written, check it out!)

Attributes on objects weren't treated directly in the original λ_JS. In 5th Edition, they are crucial to several security-relevant operations on objects. For example, the standard specifies Object.freeze(), which makes an object's properties forever unwritable. S5 directly models the writable and configurable attributes that make this operation possible, and make its implementation in S5 easy to understand.

λ_JS explicitly elided eval() from its semantics. S5 implements eval() by performing desugaring within the interpreter and then interpreting the desugared code. We implement only the strict mode version of eval, which restricts the environment that the eval'd code can affect. With these restrictions, we can implement eval in a straightforward way within our interpreter. We'll cover the details of how we do this, and why it works, in another post.

Building on S5

There's a ton we can do with S5. More, in fact, than we can do by ourselves:

Experiment with Harmony features: ECMAScript 6, or Harmony, as it is often called, is being designed right now. Proxies, string interpolation, syntactic sugar for classes, and modules are just a few of the upcoming features. Modeling them in S5 would help us understand these features better as they get integrated into the language.
Build Verification Tools: Verification based on objects' attributes is an interesting research problem―what can we prove about interacting programs if we know about unwritable fields and inextensible objects? Building this knowledge into a type-checker or a program analysis could give interesting new guarantees.
Abstract Our Machine: Matt Might and David van Horn wrote about abstracting λ_JS for program analysis. We've added new constructs to the language since then. Do they make abstraction any harder?
Complete the Implementation: We've made a lot of progress, but there's still more ground to cover. We need support for more language features, like JSON and regular expressions, that would move our implementation along immensely. We'll work on this more, but anyone who wants to get involved is welcome to help.

If any of this sounds interesting, or if you're just curious, go ahead and check out S5! It's open source and lives in a Github repository. Let us know what you do with it!

The Essence of JavaScript

Tags: JavaScript, Semantics, Programming Languages

Posted on 29 September 2011.

Back in 2008, the group decided to really understand JavaScript. Arjun had built a static analysis for JavaScript from scratch. Being the honest chap that he is, he was forced to put the following caveat into the paper:

"We would like to formally prove that our analysis is sound. A sound analysis would guarantee that our tool will never raise a false alarm, an imporant usability concern. However, a proof of soundness would require a formal semantics for JavaScript and the DOM in browsers, and this does not exist."

A "formal semantics for JavaScript [...] does not exist"? Didn't he know about the official documents on such matters, the ECMAScript standard? ECMAScript 3rd edition, the standard at the time, was around 180 pages long, written in prose and pseudocode. Reading it didn't help much. It includes gems such as this description of the switch statement:

1.  Let A be the list of CaseClause items in the first
    CaseClauses, in source text order.
2.  For the next CaseClause in A, evaluate CaseClause. If there is
    no such CaseClause, go to step 7.
3.  If input is not equal to Result(2), as defined by the !== 
    operator, go to step 2.
4.  Evaluate the StatementList of this CaseClause.
5.  If Result(4) is an abrupt completion then return Result(4).
6.  Go to step 13.
7.  Let B be the list of CaseClause items in the second
    CaseClauses, in source text order.
8.  For the next CaseClause in B, evaluate CaseClause. If there is
    no such CaseClause, go to step 15.
9.  If input is not equal to Result(8), as defined by the !== 
    operator, go to step 8.
10. Evaluate the StatementList of this CaseClause.
11. If Result(10) is an abrupt completion then return Result(10).
12. Go to step 18.
...

And this is just one of 180 pages of lesser or greater eloquence. With this as his formal reference, it's no wonder Arjun had a hard time making soundness claims.

Around the same time, Ankur Taly, Sergio Maffeis, and John Mitchell noticed the same problem. They presented a formal semantics for JavaScript in their APLAS 2008 paper. You can find their semantics here, and it is a truly staggering effort, running for 40+ pages (that's at least four times easier to understand!). However, we weren't quite satisfied. Their semantics formalizes the ECMAScript specification as written, and therefore inherits some of its weirdness, such as heap-allocated "scope objects", implicit coercions, etc. We still couldn't build tools over it, and were unwilling to do 40-page case analyses for proofs. Leo Meyerovich, peon extraordinaire and friend of the blog, felt the same:

"Challenging current attempts to analyze JavaScript, there is no formal semantics realistic enough to include many of the attack vectors we have discussed yet structured and tractable enough that anyone who is not the inventor has been able to use; formal proofs are therefore beyond the scope of this work."

How To Tackle JavaScript: The PLT Way

We decided to start smaller. In the fall of 2009, Arjun wrote down a semantics for the "core" of JavaScript that fits on just three pages (that's 60 times easier to understand!). This is great programming languages research—we defined away the hairy parts of the problem and focused on a small core that was amenable to proof. For these proofs, we could assume the existence of a trivial desugaring that maps real JavaScript programs into programs in the core semantics, which Arjun dubbed λ_JS.

Things were looking great until one night Arjun had a few too many glasses of wine and decided to implement desugaring. Along with Claudiu Saftoiu, he wrote a thousand lines of Haskell that turns JavaScript programs into λ_JS programs. Even worse, they implemented an interpreter for λ_JS, so the resulting programs actually run. They had therefore produced a JavaScript runtime.

Believe it or not, there are other groups in the business of creating JavaScript runtimes, namely Google, Mozilla, Microsoft, and a few more. And since they care about the correctness of their implementations, they have actual test suites. Which Arjun's system could run, and give answers for, that may or may not be the right ones:

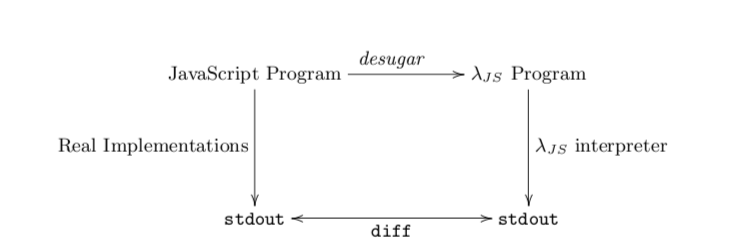
As it turns out, Arjun and Claudiu did a pretty good job. λ_JS agrees with Mozilla SpiderMonkey on a few thousand lines of tests. We say "agreed" and not "passed" because SpiderMonkey fails some of its own tests. Without any other standard of correctness, λ_JS strives for bug-compatibility with SpiderMonkey on those tests.

Building on λ_JS

λ_JS is discussed in our ECOOP paper, but it's the work built on λ_JS that's most interesting. We've built the following systems ourselves:

A type-checker for JavaScript that employs a novel mix of type-checking and flow analysis ("flow typing"), discussed in our ESOP 2011 paper, and
An extension to the above type-checker to verify ADsafe, as discussed in our USENIX Security 2011 paper.

Others have built on λ_JS too:

David van Horn and Matt Might use λ_JS to build an analytic framework for JavaScript,
Rodolfo Toledo and Éric Tanter use λ_JS to specify aspects for JavaScript,
IBEX, from Microsoft Research, uses λ_JS for its JavaScript backend to produce verified Web browser extensions, and
Others have a secret reimplementation of λ_JS in Java. We are now enterprise-ready.

Want to use λ_JS to write JavaScript tools? Check out our software and let us know what you think!

Coming up next: The latest version of JavaScript, ECMAScript 5th ed., is vastly improved. We've nearly finished updating our JavaScript semantics to match ECMAScript 5th ed. Our new semantics uses the official ECMAScript test suite and tackles problems, such as eval, that the original λ_JS elided. We'll talk about it next time. Update: We've written about our update, dubbed S5, its semantics for accessors, and a particularly interesting example.

The Brown PLT Blog

Articles by tag: Semantics

First Perspective

Second Perspective

Third Perspective

How it Works

What’s going on right now, and what’s next?

Resugaring Explained

Formal Properties of Resugaring

The Problem

The Ordinary Solution

The Extraordinary Solution

Lessons about JavaScript

Takeaway

The Paper

Updating Subtyping

Giving Types to Values

Capturing the Whole Table

First-class Singleton Strings

String Pattern Types

Subtyping

Quiz Time!

Capturing all the Evals

Engineering eval

Leveraging S5's Eval

Progressive Types

What makes this event programming so special?

What Could Possibly Go Wrong?

Modeling Event Dispatch

What’s Done

What’s Next

Recap: The Structure of λJS

PLT Redex: Lightweight Mechanization

Coq: A Machine-Checked Proof

What's Done

What's Next

Dictionaries with Inheritance

Classes Do Not Shape Objects

Methods?

But Why?

So?

The Innocuous +

If You Can't Beat 'Em...

A Malleable Implementation

More than λJS

Building on S5

How To Tackle JavaScript: The PLT Way

Building on λJS

Engineering `eval`

Recap: The Structure of λ_JS

More than λ_JS

Building on λ_JS