Articles by tag: Programming Languages
Resugaring Type Rules
Can We Crowdsource Language Design?
A Third Perspective on Hygiene
Scope Inference, a.k.a. Resugaring Scope Rules
The Pyret Programming Language: Why Pyret?
Resugaring Evaluation Sequences
Slimming Languages by Reducing Sugar
Tierless Programming for SDNs: Differential Analysis
Tierless Programming for SDNs: Verification
Tierless Programming for SDNs: Optimality
Tierless Programming for SDNs: Events
Tierless Programming for Software-Defined Networks
Verifying Extensions’ Compliance with Firefox's Private Browsing Mode
From MOOC Students to Researchers
(Sub)Typing First Class Field Names
Typing First Class Field Names
S5: Engineering Eval
Progressive Types
Mechanized LambdaJS
Objects in Scripting Languages
S5: Wat?
S5: Semantics for Accessors
S5: A Semantics for Today's JavaScript
The Essence of JavaScript
ADsafety
Mystery Languages
Tags: Programming Languages, Education
Posted on 05 July 2018.How do you learn a new language? Do you simply read its reference manual, and then you’re good to go? Or do you also explore the language, trying things out by hand to see how they behave?
This skill—learning about something by poking at it—is frequently used but almost never taught. However, we have tried to teach it via what we dub mystery languages, and this post is about how we went about it.
Mystery Lanuages
A mystery language is exactly what it sounds like: a programming language whose behavior is a mystery. Each assignment comes with some vague documentation, and an editor in which you can write programs. However, when you run a program it will produce multiple answers! This is because there are actually multiple languages, with the same syntax but different semantics. The answers you get are the results of running your program in all of the different languages. The goal of the assignment is to find programs that tell the languages apart.
As an example, maybe the languages have the syntax a[i], and the
documentation says that this “accesses an array a at index i”.
That totally specifies the behavior of this syntax, right?
Not even close. For example, what happens if the index is out of bounds?
Does it raise an error (like Java), or return undefined (like
JavaScript), or produce nonsense (like C), or wrap the index to a
valid one (like Python)? And what happens if the index is 2.5, or
"2", or 2.0, or "two"?
(EDIT: Specifically, Python wraps negative indices that are smaller than the length of the array.)
Students engage with the mystery languages in three ways:
- The first part of each assignment is to find a set of programs that distinguishes the different languages (a.k.a. a classifier).
- The second part of the assignment is to describe a theory that explains the different behaviors of the languages. (For example, a theory about C’s behavior could include accessing heap addresses past the end of an array.)
- Finally, after an assignment is due, there’s an in-class discussion and explanation of the mystery languages. This is especially useful to provide terminology for behaviors that students encountered in the languages.
This example is somewhat superficial (the real mystery languages mostly use more significant features than array access), but you get the idea: every aspect of a programming language comes with many possible designs, and the mystery languages have students explore them first-hand.
Why Mystery Languages?
We hope to teach a number of skills through mystery languages:
- Evaluating Design Decisions: The mystery languages are almost entirely based on designs chosen by real languages: either historical choices that have since been settled, or choices that are still up in the air and vary between modern languages. Students get to explore the consequences of these decisions themselves, so that they get a feel for them. And the next day in class they learn about the broader historical context.
- Syntax vs. Semantics: We are frustrated by how frequently discussions about programming languages revolve around syntax. With luck, showing students first-hand that a single syntax can have a variety of semantics will bring their discussions to a somewhat higher level.
- Adversarial Thinking: Notice that the array example was all about exploring edge cases. If you only ever wrote correct, safe, boring programs then you’d never notice the different ways that array access could work. This is very similar to the kind of thinking you need to do when reasoning about security, and we hope that students might pick up on this mindset.
- Experimental Thinking: In each assignment, students are asked not only to find programs that behave differently across the mystery languages, but also to explain the behavior of the different languages. This is essentially a scientific task: brainstorm hypotheses about how the languages might work; experimentally test these hypotheses by running programs; discard any hypothesis that was falsified; and iterate.
Adopting Mystery Languages
If you want to use Mystery Languages in your course, email us and we’ll help you get started!
There are currently 13 mystery languages, and more in development. At Brown, we structured our programming languages course around these mystery languages: about half of the assignments and half of the lectures were about mystery languages. However, mystery languages are quite flexible, and could also be used as a smaller supplement to an existing course. One possibility is to begin with one or two simpler languages to allow students to learn how they work, and from there mix and match any of the more advanced languages. Alternatively, you could do just one or two mystery languages to meet specific course objectives.
Learn More
You can learn more about mystery languages in our SNAPL’17 paper, or dive in and try them yourself (see the assignments prefixed with “ML:”).
Resugaring Type Rules
Tags: Programming Languages, Types
Posted on 19 June 2018.This is the final post in a series about resugaring. It focuses on resugaring type rules. See also our posts on resugaring evaluation steps and resugaring scope rules.
No one should have to see the insides of your macros. Yet type errors
often reveal them. For example, here is a very simple and macro in
Rust (of course you should just use && instead, but we’ll use this
as a simple working example):

and the type error message you get if you misuse it:
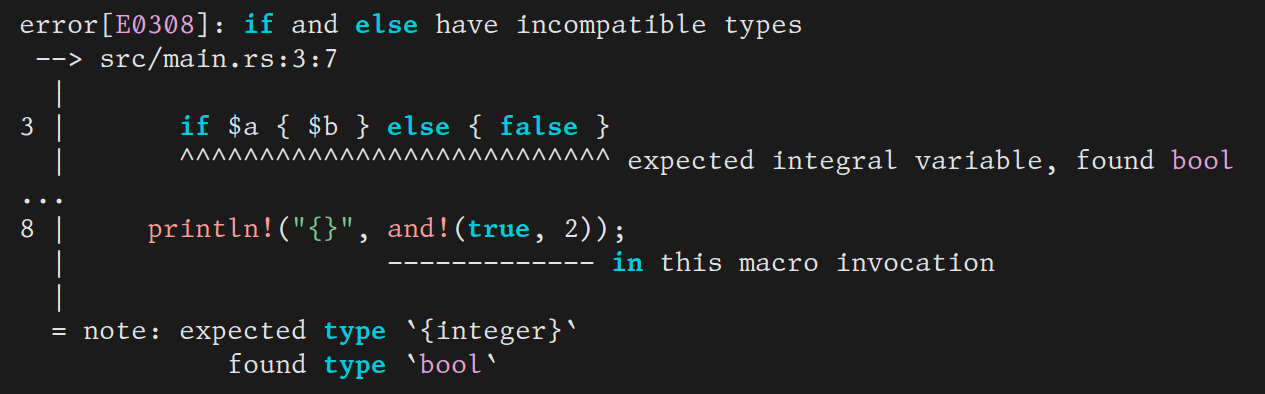
You can see that it shows you the definition of this macro. In this case it’s not so bad, but other macros can get messy, and you might not want to see their guts. Plus in principle, a type error should only show the erronous code, not correct code that it happend to call. You wouldn’t be very happy with a type checker that sometimes threw an error deep in the body of a (type correct) library function that you called, just because you used it the wrong way. Why put up with one that does the same thing for macros?
The reason Rust does is that that it does not know the type of and.
As a result, it can only type check after and has been desugared
(a.k.a., expanded), and so the error occurs in the desugared code.
But what if Rust could automatically infer a type rule for checking
and, using only the its definition? Then the error could be found in
the original program that you wrote (rather than its expansion), and
presented as such. This is exactly what we did—albeit for simpler type
systems than Rust’s—in our recent PLDI’18 paper
Inferring Type Rules for Syntactic Sugar.
We call this process resugaring type rules; akin to our previous work
on
resugaring evaluation steps
and
resugaring scope rules.
Let’s walk through the resugaring of a type rule for and:
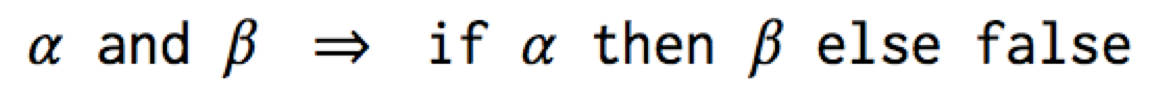
We want to automatically derive a type rule for and, and we want it
to be correct. But what does it mean for it to be correct? Well, the
meaning of and is defined by its desugaring: α and β is synonymous
with if α then β else false. Thus they should have the same type:
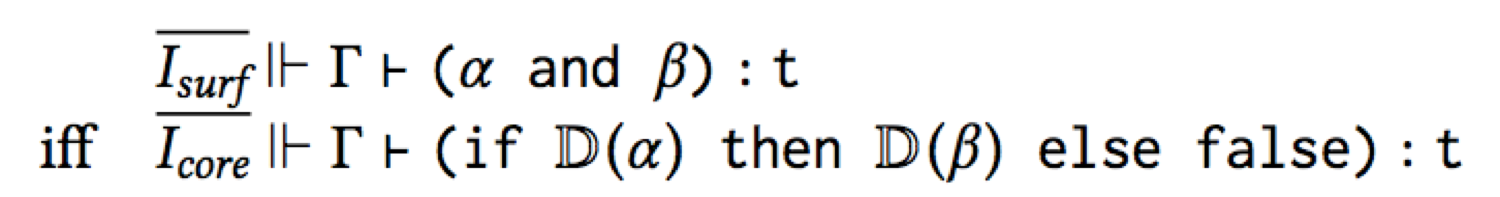
(Isurf ||- means “in the surface language type system”, Icore
||- means “in the core language type system”, and the fancy D means
“desugar”.)
How can we achieve this? The most straightforward to do is to capture
the iff with two type rules, one for the forward implication, and
one for the reverse:
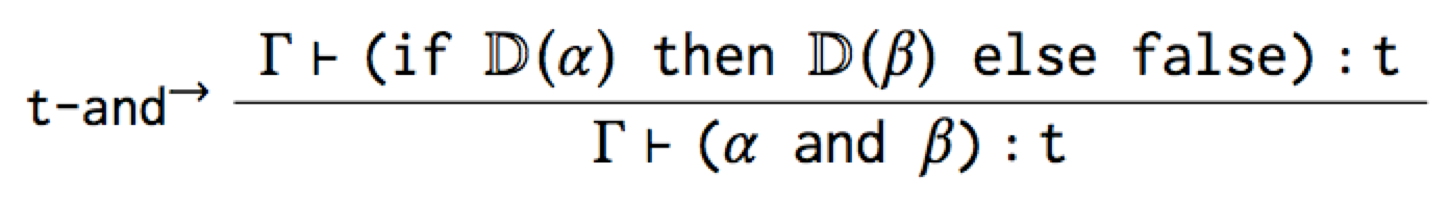
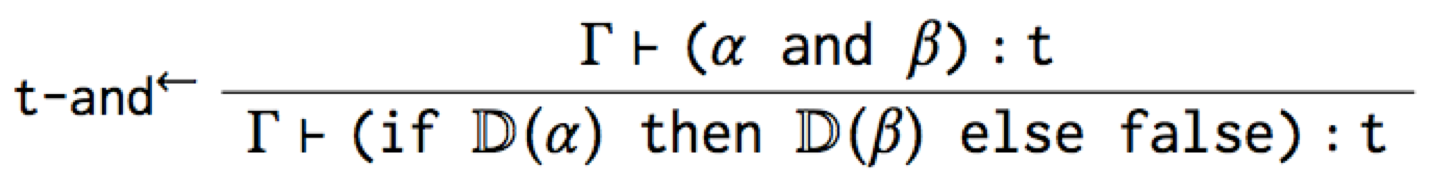
The first type rule is useful because it says how to type check and
in terms of its desugaring. For example, here’s a derivation that
true and false has type Bool:

However, while this t-and→ rule is accurate, it’s not the canonical
type rule for and that you’d expect. And worse, it mentions if, so
it’s leaking the implementation of the macro!
However, we can automatically construct a better type rule. The trick
is to look at a more general derivation. Here’s a generic type
derivation for any term α and β:
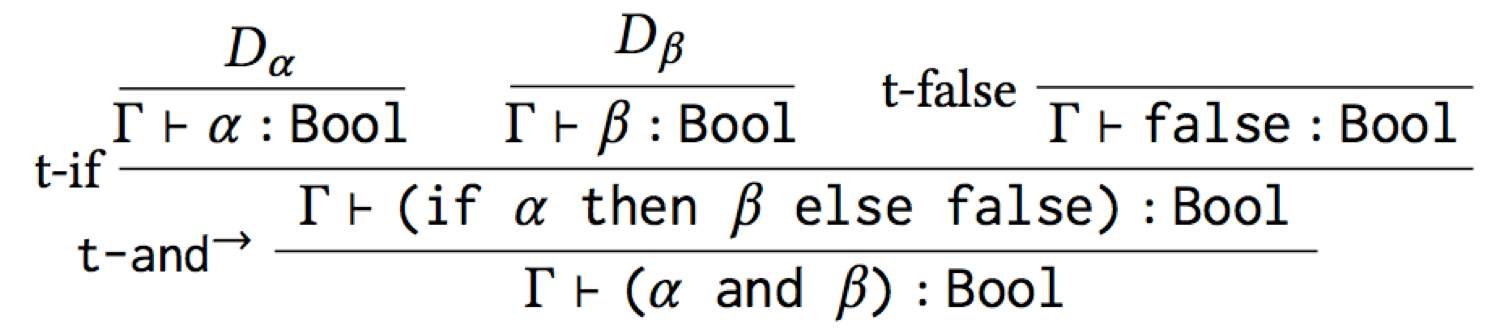
Notice Dα and Dβ: these are holes in the derivation, which ought to be filled in with sub-derivations proving that α has type Bool and β has type Bool. Thus, “α : Bool” and “β : Bool” are assumptions we must make for the type derivation to work. However, if these assumptions hold, then the conclusion of the derivation must hold. We can capture this fact in a type rule, whole premises are these assumptions, and whose conclusion is the conclusion of the whole derivation:
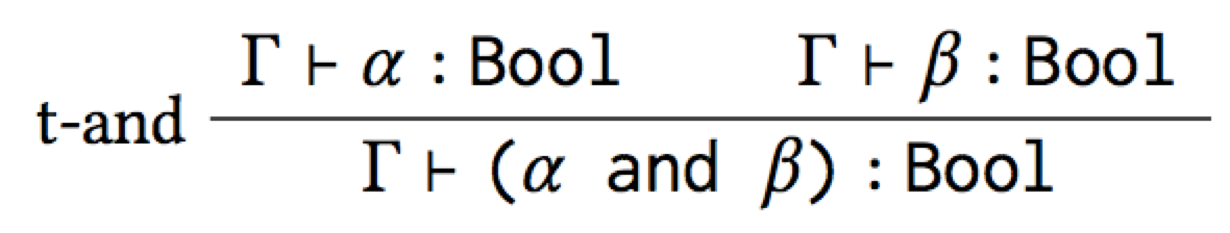
And so we’ve inferred the canonical type rule for and! Notice that
(i) it doesn’t mention if at all, so it’s not leaking the inside of
the macro, and (ii) it’s guaranteed to be correct, so it’s a good
starting point for fixing up a type system to present errors at the
right level of abstraction. This was a simple example for illustrative
purposes, but we’ve tested the approach on a variety of sugars and
type systems.
You can read more in our paper, or play with the implementation.
Can We Crowdsource Language Design?
Tags: Programming Languages, User Studies, Semantics
Posted on 06 July 2017.Programming languages are user interfaces. There are several ways of making decisions when designing user interfaces, including:
- a small number of designers make all the decisions, or
- user studies and feedback are used to make decisions.
Most programming languages have been designed by a Benevolent Dictator for Life or a committee, which corresponds to the first model. What happens if we try out the second?
We decided to explore this question. To get a large enough number of answers (and to engage in rapid experimentation), we decided to conduct surveys on Amazon Mechanical Turk, a forum known to have many technically literate people. We studied a wide range of common programming languages features, from numbers to scope to objects to overloading behavior.
We applied two concrete measures to the survey results:
- Consistency: whether individuals answer similar questions the same way, and
- Consensus: whether we find similar answers across individuals.
Observe that a high value of either one has clear implications for language design, and if both are high, that suggests we have zeroed in on a “most natural” language.
As Betteridge’s Law suggests, we found neither. Indeed,
-
A surprising percentage of workers expected some kind of dynamic scope (83.9%).
-
Some workers thought that record access would distribute over the field name expression.
-
Some workers ignored type annotations on functions.
-
Over the field and method questions we asked on objects, no worker expected Java’s semantics across all three.
These and other findings are explored in detail in our paper.
A Third Perspective on Hygiene
Tags: Programming Languages, Semantics
Posted on 20 June 2017.In the last post, we talked about scope inference: automatically inferring scoping rules for syntatic sugar. In this post we’ll talk about the perhaps surprising connection between scope inference and hygiene.
Hygiene can be viewed from a number of perspectives and defined in a number of ways. We’ll talk about two pre-existing perspectives, and then give a third perspective that comes from having scope inference.
First Perspective
The traditional perspective on hygiene (going all the way back to Kohlbecker in ’86) defines it by what shouldn’t happen when you expand macros / syntactic sugar. To paraphrase the idea:
Expanding syntactic sugar should not cause accidental variable capture. For instance, a variable used in a sugar should not come to refer to a variable declared in the program simply because it has the same name.
Thus, hygiene in this tradition is defined by a negative.
It has also traditionally focused strongly on algorithms. One would expect papers on hygiene to state a definition of hygiene, give an algorithm for macro expansion, and then prove that the algorithm obeys these properties. But this last step, the proof, is usually suspiciously missing. At least part of the reason for this, we suspect, is that definitions of hygiene have been too informal to be used in a proof.
And a definition of hygiene has been surprisingly hard to pin down precisely. In 2015, a full 29 years after Kohlbecker’s seminal work, Adams writes that “Hygiene is an essential aspect of Scheme’s macro system that prevents unintended variable capture. However, previous work on hygiene has focused on algorithmic implementation rather than precise, mathematical definition of what constitutes hygiene.” He goes on to discuss “observed-binder hygiene”, which is “not often discussed but is implicitly averted by traditional hygiene algorithms”. The point we’re trying to make is that the traditional view on hygiene is subtle.
Second Perspective
There is a much cleaner definition of hygiene, however, that is more of a positive statement (and subsumes the preceding issues):
If two programs are α-equivalent (that is, they are the same up to renaming variables), then when you desugar them (that is, expand their sugars) they should still be α-equivalent.
Unfortunately, this definition only makes sense if we have scope defined on both the full and base languages. Most hygiene systems can’t use this definition, however, because the full language is not usually given explicit scoping rules; rather, it’s defined implicitly through translation into the base language.
Recently, Herman and Wand have advocated for specifying the scoping rules for the full language (in addition to the base language), and then verifying that this property holds. If the property doesn’t hold, then either the scope specification or the sugar definitions are incorrect. This is, however, an onerous demand to place on the developer of syntactic sugar, especially since scope can be surprisingly tricky to define precisely.
Third Perspective
Scope inference gives a third perspective. Instead of requiring authors of syntactic sugar to specify the scoping rules for the full language, we give an algorithm that infers them. We have to then define what it means for this algorithm to work “correctly”.
We say that an inferred scope is correct precisely if the second definition of hygiene holds: that is, if desugaring preserves α-equivalence. Thus, our scope inference algorithm finds scoping rules such that this property holds, and if no such scoping rules exist then it fails. (And if there are multiple sets of scoping rules to choose from, it chooses the ones that put as few names in scope as possible.)
An analogy would be useful here. Think about type inference: it finds type annotations that could be put in your program such that it would type check, and if there are multiple options then it picks the most general one. Scope inference similarly finds scoping rules for the full language such that desugaring preserves α-equivalence, and if there are multiple options then it picks the one that puts the fewest names in scope.
This new perspective on hygiene allows us to shift the focus from expansion algorithms to the sugars themselves. When your focus is on an expansion algorithm, you have to deal with whatever syntactic sugar is thrown your way. If a sugar introduces unbound identifiers, then the programmer (who uses the macro) just has to deal with it. Likewise, if a sugar uses scope inconsistently, treating a variable either as a declaration or a reference depending on the phase of the moon, the programmer just has to deal with it. In contrast, since we infer scope for the full language, we check check weather a sugar would do one of these bad things, and if so we can call the sugar unhygienic.
To be more concrete, consider a desugaring
rule for bad(x, expression) that sometimes expands
to lambda x: expression and sometimes expands to just expression,
depending on the context. Our algorithm would infer from the first
rewrite that the expression must be in scope of x. However, this would
mean that the expression was allowed to contain references to x,
which would become unbound when the second rewrite was used! Our
algorithm detects this and rejects this desugaring rule. Traditional
macro systems allow this, and only detect the potential unbound
identifier problem when it actually occurred. The paper contains a
more interesting example called “lambda flip flop” that is rejected
because it uses scope inconsistently.
Altogether, scope inference rules out bad sugars that cannot be made hygienic, but if there is any way to make a sugar hygienic it will find it.
Again, here’s the paper and implementation, if you want to read more or try it out.
Scope Inference, a.k.a. Resugaring Scope Rules
Tags: Programming Languages, Semantics
Posted on 12 June 2017.This is the second post in a series about resugaring. It focuses on resugaring scope rules. See also our posts on resugaring evaluation steps and resugaring type rules.
Many programming languages have syntactic sugar. We would hazard to
guess that most modern languages do. This is when a piece of syntax
in a language is defined in terms of the rest of the language. As a
simple example, x += expression might be shorthand for x = x +
expression. A more interesting sugar is
Pyret’s for loops.
For example:
for fold(p from 1, n from range(1, 6)):
p * n
end
computes 5 factorial, which is 120. This for is a piece of sugar,
though, and the above code is secretly shorthand for:
fold(lam(p, n): p * n end, 1, range(1, 6))
Sugars like this are great for language development: they let you grow a language without making it more complicated.
Languages also have scoping rules that say where variables are in scope. For instance, the scoping rules should say that a function’s parameters are in scope in the body of the function, but not in scope outside of the function. Many nice features in editors depend on these scoping rules. For instance, if you use autocomplete for variable names, it should only suggest variables that are in scope. Similarly, refactoring tools that rename variables need to know what is in scope.
This breaks down in the presence of syntactic sugar, though: how can your editor tell what the scoping rules for a sugar are?
The usual approach is to write down all of the scoping rules for all of the sugars. But this is error prone (you need to make sure that what you write down matches the actual behavior of the sugars), and tedious. It also goes against a general principle we hold: to add a sugar to a language, you should just add the sugar to the language. You shouldn’t also need to update your scoping rules, or update your type system, or update your debugger: that should all be done automatically.
We’ve just published a paper at ICFP that shows how to automatically
infer the scoping rules for a piece of sugar, like the for example
above. Here is the
paper and implementation.
This is the latest work we’ve done with the goal of making the above
principle a reality. Earlier, we showed
how to automatically find evaluation steps that show how your program
runs in the presence of syntatic sugar.
How it Works
Our algorithm needs two things to run:
- The definitions of syntactic sugar. These are given as pattern-based rewrite rules, saying what patterns match and what they should be rewritten to.
- The scoping rules for the base (i.e. core) language.
It then automatically infers scoping rules for the full language, that includes the sugars. The final step to make this useful would be to add these inferred scoping rules to editors that can use them, such as Sublime, Atom, CodeMirror, etc.
For example, we have tested it on Pyret (as well as other languages).
We gave it scoping rules for Pyret’s base language (which included
things like lambdas and function application), and we gave it rules
for how for desugars, and it determined the scoping rules of
for. In particular:
- The variables declared in each
fromclause are visible in the body, but not in the argument of anyfromclause. - If two
fromclauses both declare the same variable, the second one shadows the first one.
This second rule is exactly the sort of thing that is easy to overlook if you try to write these rules down by hand, resulting in obscure bugs (e.g. when doing automatic variable refactoring).
Here are the paper and implementation, if you want to read more or try it out.
The Pyret Programming Language: Why Pyret?
Tags: Education, Programming Languages, Semantics
Posted on 26 June 2016.We need better languages for introductory computing. A good introductory language makes good compromises between expressiveness and performance, and between simplicity and feature-richness. Pyret is our evolving experiment in this space.
Since we expect our answer to this question will evolve over time, we’ve picked a place for our case for the language to live, and will update it over time:
The Pyret Code; or A Rationale for The Pyret Programming Language
The first version answers a few questions that we expect many people have when considering languages in general and languages for education in particular:
- Why not just use Java, Python, Racket, OCaml, or Haskell?
- Will Pyret ever be a full-fledged programming language?
- But there are lots of kinds of “education”!
- What are some ways the educational philosophy influences the langauge?
In this post, it’s worth answering one more immediate question:
What’s going on right now, and what’s next?
We are currently hard at work on three very important features:
-
Support for static typing. Pyret will have a conventional type system with tagged unions and a type checker, resulting in straightforward type errors without the complications associated with type inference algorithms. We have carefully designed Pyret to always be typeable, but our earlier type systems were not good enough. We’re pretty happy with how this one is going.
-
Tables are a critical type for storing real-world data. Pyret is adding linguistic and library support for working effectively with tables, which PAPL will use to expose students to “database” thinking from early on.
-
Our model for interactive computation is based on the “world” model. We are currently revising and updating it in a few ways that will help it better serve our new educational programs.
On the educational side, Pyret is already used by the Bootstrap project. We are now developing three new curricula for Bootstrap:
-
A CS1 curriculum, corresponding to a standard introduction to computer science, but with several twists based on our pedagogy and materials.
-
A CS Principles curriculum, for the new US College Board Advanced Placement exam.
-
A physics/modeling curriculum, to help teach students physics and modeling through the medium of programming.
If you’d like to stay abreast of our developments or get involved in our discussions, please come on board!
Resugaring Evaluation Sequences
Tags: Programming Languages, Semantics
Posted on 06 February 2016.This is the first post in a series about resugaring. It focuses on resugaring evaluation sequences. See also our later posts on resugaring scope rules and resugaring type rules.
A lot of programming languages are defined in terms of syntactic sugar. This has many advantages, but also a couple of drawbacks. In this post, I’m going to tell you about one of these drawbacks, and the solution we found for it. First, though, let me describe what syntactic sugar is and why it’s used.
Syntactic sugar is when you define a piece of syntax in a language in
terms of the rest of the language. You’re probably already familiar
with many examples. For instance, in Python, x + y is syntactic
sugar for x.__add__(y). I’m going to use the word “desugaring”
to mean the expansion of syntactic sugar, so I’ll say that x + y
desugars to x.__add__(y). Along the same lines, in
Haskell, [f x | x <- lst] desugars to map f lst. (Well, I’m
simplifying a little bit; the full desugaring is given by the
Haskell 98 spec.)
As a programming language researcher I love syntactic sugar, and you should too. It splits a language into two parts: a big “surface” language that has the sugar, and a much smaller “core” language that lacks it. This separation lets programmers use the surface language that has all of the features they know and love, while letting tools work over the much simpler core language, which lets the tools themselves be simpler and more robust.
There’s a problem, though (every blog post needs a problem). What happens when a tool, which has been working over the core language, tries to show code to the programmer, who has been working over the surface? Let’s zoom in on one instance of this problem. Say you write a little snippet of code, like so: (This code is written in an old version of Pyret; it should be readable even if you don’t know the language.)
my-list = [2]
cases(List) my-list:
| empty() => print("empty")
| link(something, _) =>
print("not empty")
end
And now say you’d like to see how this code runs. That is, you’d like to see an evaluation sequence (a.k.a. an execution trace) of this program. Or maybe you already know what it will do, but you’re teaching students, and would like to show them how it will run. Well, what actually happens when you run this code is that it is first desugared into the core, like so:
my-list = list.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({
"empty" : fun(): print("empty") end,
"link" : fun(something, _):
print("not empty") end
},
fun(): raise("cases: no cases matched") end)
end
This core code is then run (each block of code is the next evaluation step):
my-list = obj.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
my-list = obj.["link"](2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
my-list = <func>(2, list.["empty"])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
my-list = <func>(2, obj.["empty"])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
my-list = <func>(2, obj.["empty"])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
my-list = <func>(2, [])
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
my-list = [2]
block:
tempMODRIOUJ :: List = my-list
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end,
"link" : fun(something, _): print("not empty") end}, fun():
raise("cases: no cases matched") end)
end
tempMODRIOUJ :: List = [2]
tempMODRIOUJ.["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)
[2].["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)
[2].["_match"]({"empty" : fun(): print("empty") end, "link" :
fun(something, _): print("not empty") end}, fun(): raise("cases: no
cases matched") end)
<func>({"empty" : fun(): end, "link" : fun(something, _): print("not
empty") end}, fun(): raise("cases: no cases matched") end)
<func>({"empty" : fun(): end, "link" : fun(): end}, fun():
raise("cases: no cases matched") end)
<func>(obj, fun(): raise("cases: no cases matched") end)
<func>(obj, fun(): end)
<func>("not empty")
"not empty"
But that wasn’t terribly helpful, was it? Sometimes you want to see exactly what a program is doing in all its gory detail (along the same lines, it’s occasionally helpful to see the assembly code a program is compiling to), but most of the time it would be nicer if you could see things in terms of the syntax you wrote the program with! In this particular example, it would be much nicer to see:
my-list = [2]
cases(List) my-list:
| empty() => print("empty")
| link(something, _) =>
print("not empty")
end
my-list = [2]
cases(List) my-list:
| empty() => print("empty")
| link(something, _) =>
print("not empty")
end
cases(List) [2]:
| empty() => print("empty")
| link(something, _) =>
print("not empty")
end
<func>("not empty")
"not empty"
(You might have noticed that the first step got repeated for what
looks like no reason. What happened there is that the code [2]
was evaluated to an actual list, which also prints itself as [2].)
So we built a tool that does precisely this. It turns core evaluation sequences into surface evaluation sequences. We call the process resugaring, because it’s the opposite of desugaring: we’re adding the syntactic sugar back into your program. The above example is actual output from the tool, for an old version of Pyret. I’m currently working on a version for modern Pyret.
Resugaring Explained
I always find it helpful to introduce a diagram when explaining resugaring. On the right is the core evaluation sequence, which is the sequence of steps that the program takes when it actually runs. And on the left is the surface evaluation sequence, which is what you get when you try to resugar each step in the core evaluation sequence. As a special case, the first step on the left is the original program.
Here’s an example. The starting program will be not(true) or true, where
not is in the core language, but or is defined as a piece of
sugar:
x or y ==desugar==> let t = x in
if t then t else y
And here’s the diagram:

The steps (downarrows) in the core evaluation sequence are ground
truth: they are what happens when you actually run the program. In
contrast, the steps in the surface evaluation sequence
are made up; the whole surface evaluation sequence is an attempt at
reconstructing a nice evaluation sequence by resugaring each of the
core steps. Notice that the third core term fails to resugar. This is
because there’s no good way to represent it in terms of or.
Formal Properties of Resugaring
It’s no good to build a tool without having a precise idea of what it’s supposed to do. To this end, we came up with three properties that (we think) capture exactly what it means for a resugared evaluation sequence to be correct. It will help to look at the diagram above when thinking about these properties.
-
Emulation says that every term on the left should desugar to the term to its right. This expresses the idea that the resugared terms can’t lie about the term they’re supposed to represent. Another way to think about this is that desugaring and resugaring are inverses.
-
Abstraction says that the surface evaluation sequence on the left should show a sugar precisely when the programmer used it. So, for example, it should show things using
orand notlet, because the original program usedorbut notlet. -
Coverage says that you should show as many steps as possible. Otherwise, technically the surface evaluation sequence could just be empty! That would satisfy both Emulation and Abstraction, which only say things about the steps that are shown.
We’ve proved that our resugaring algorithm obeys Emulation and Abstraction, and given some good emperical evidence that it obeys Coverage too.
I’ve only just introduced resugaring. If you’d like to read more, see the paper, and the followup that deals with hygiene (e.g., preventing variable capture).
Slimming Languages by Reducing Sugar
Tags: JavaScript, Programming Languages, Semantics
Posted on 08 January 2016.JavaScript is a crazy language. It’s defined by 250 pages of English prose, and even the parts of the language that ought to be simple, like addition and variable scope, are very complicated. We showed before how to tackle this problem using λs5, which is an example of what’s called a tested semantics.
You can read about λs5 at the above link. But the basic idea is that λs5 has two parts:
- A small core language that captures the essential parts of JavaScript, without all of its foibles, and
- A desugaring function that translates the full language down to this small core.
(We typically call this core language λs5, even though technically speaking it’s only part of what makes up λs5.)
These two components together give us an implementation of JavaScript:
to run a program, you desugar it to λs5, and then
run that program. And with this implementation, we can run
JavaScript’s conformance test suite to check that
λs5 is accurate: this is why it’s called a tested
semantics. And lo, λs5 passes the relevant portion
of the test262 conformance suite.
The Problem
Every blog post needs a problem, though. The problem with λs5 lies in desugaring. We just stated that JavaScript is complicated, while the core language for λs5 is simple. This means that the complications of JavaScript must be dealt with not in the core language, but instead in desugaring. Take an illustrative example. Here’s a couple of innocent lines of JavaScript:
function id(x) {
return x;
}
These couple lines desugar into the following λs5 code:
{let
(%context = %strictContext)
{ %defineGlobalVar(%context, "id");
{let
(#strict = true)
{"use strict";
{let
(%fobj4 =
{let
(%prototype2 = {[#proto: %ObjectProto,
#class: "Object",
#extensible: true,]
'constructor' : {#value (undefined) ,
#writable true ,
#configurable false}})
{let
(%parent = %context)
{let
(%thisfunc3 =
{[#proto: %FunctionProto,
#code: func(%this , %args)
{ %args[delete "%new"];
label %ret :
{ {let
(%this = %resolveThis(#strict,
%this))
{let
(%context =
{let
(%x1 = %args
["0" , null])
{[#proto: %parent,
#class: "Object",
#extensible: true,]
'arguments' : {#value (%args) ,
#writable true ,
#configurable false},
'x' : {#getter func
(this , args)
{label %ret :
{break %ret %x1}} ,
#setter func
(this , args)
{label %ret :
{break %ret %x1 := args
["0" , {[#proto: %ArrayProto,
#class: "Array",
#extensible: true,]}]}}}}})
{break %ret %context["x" , {[#proto: null,
#class: "Object",
#extensible: true,]}];
undefined}}}}},
#class: "Function",
#extensible: true,]
'prototype' : {#value (%prototype2) ,
#writable true ,
#configurable true},
'length' : {#value (1.) ,
#writable true ,
#configurable true},
'caller' : {#getter %ThrowTypeError ,
#setter %ThrowTypeError},
'arguments' : {#getter %ThrowTypeError ,
#setter %ThrowTypeError}})
{ %prototype2["constructor" = %thisfunc3 , null];
%thisfunc3}}}})
%context["id" = %fobj4 ,
{[#proto: null, #class: "Object", #extensible: true,]
'0' : {#value (%fobj4) ,
#writable true ,
#configurable true}}]}}}}}
This is a bit much. It’s hard to read, and it’s hard for tools to process. But more to the point, λs5 is meant to be used by researchers, and this code bloat has stood in the way of researchers trying to adopt it. You can imagine that if you’re trying to write a tool that works over λs5 code, and there’s a bug in your tool and you need to debug it, and you have to wade through that much code just for the simplest of examples, it’s a bit of a nightmare.
The Ordinary Solution
So, there’s too much code. Fortunately there are well-known solutions to this problem. We implemented a number of standard compiler optimization techniques to shrink the generated λs5 code, while preserving its semantics. Here’s a boring list of the Semantics-Preserving optimizations we used:
- Dead-code elimination
- Constant folding
- Constant propogation
- Alias propogation
- Assignment conversion
- Function inlining
- Infer type & eliminate static checks
- Clean up unused environment bindings
Most of these are standard textbook optimizations; though the last two are specific to λs5. Anyhow, we did all this and got… 5-10% code shrinkage.
The Extraordinary Solution
That’s it: 5-10%.
Given the magnitude of the code bloat problem, that isn’t nearly enough shrinkage to be helpful. So let’s take a step back and ask where all this bloat came from. We would argue that code bloat can be partitioned into three categories:
- Intended code bloat. Some of it is intentional. λs5 is a small core language, and there should be some expansion as you translate to it.
- Incidental code bloat. The desugaring function from JS to λs5 is a simple recursive-descent function. It’s purposefully not clever, and as a result it sometimes generates redundant code. And this is exactly what the semantics-preserving rewrites we just mentioned get rid of.
- Essential code bloat. Finally, some code bloat is due to the semantics of JS. JS is a complicated langauge with complicated features, and they turn into complicated λs5 code.
There wasn’t much to gain by way of reducing Intended or Incidental code bloat. But how do you go about reducing Essential code bloat? Well, Essential bloat is the code bloat that comes from the complications of JS. To remove it, you would simplify the language. And we did exactly that! We defined five Semantics-Altering transformations:
- (IR) Identifier restoration: pretend that JS is lexically scoped
- (FR) Function restoration: pretend that JS functions are just functions and not function-object-things.
- (FA) Fixed arity: pretend that JS functions always take as many arguments as they’re declared with.
- (UAE) Assertion elimination: unsafely remove some runtime checks (your code is correct anyways, right?)
- (SAO) Simplifying arithmetic operators: eliminate strange behavior for basic operators like “+”.
These semantics-altering transformations blasphemously break the language. This is actually OK, though! The thing is, if you’re studying JS or doing static analysis, you probably already aren’t handling the whole language. It’s too complicated, so instead you handle a sub-language. And this is exactly what these semantics-altering transformations capture: they are simplifying assumptions about the JS language.
Lessons about JavaScript
And we can learn about JavaScript from them. We implemented these transformations for λs5, and so we could run the test suite with the transformations turned on and see how many tests broke. This gives a crude measure of “correctness”: a transformation is 50% correct if it breaks half the tests. Here’s the graph:
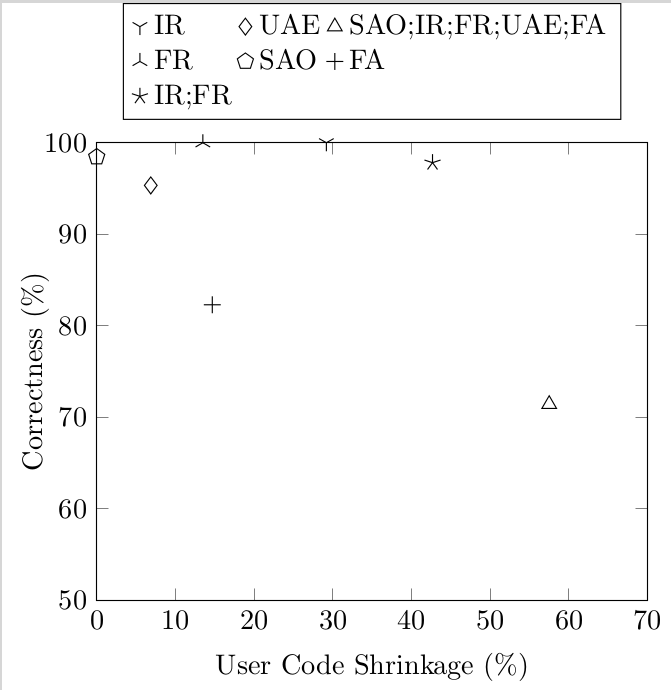
Notice that the semantics-altering transformations shrink code by more than 50%: this is way better than the 5-10% that the semantics-preserving ones gave. Going back to the three kinds of code bloat, this shows that most code bloat in λs5 is Essential: it comes from the complicated semantics of JS, and if you simplify the semantics you can make it go away.
Next, here’s the shrinkages of each of the semantics-altering transformations:
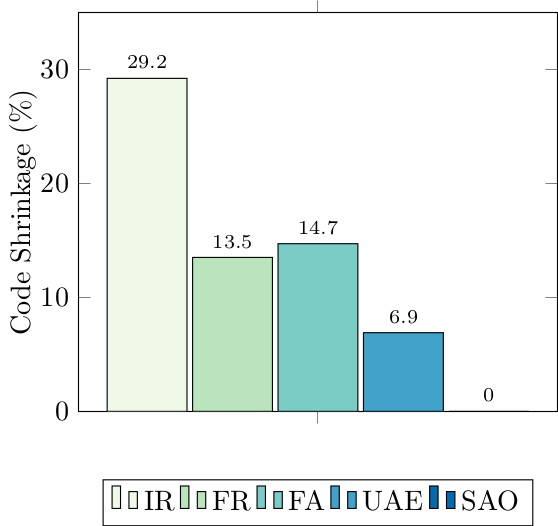
Since these semantics-altering transformations are simplifications of JS semantics, and desugared code size is a measure of complexity, you can view this graph as a (crude!) measure of complexity of language features. In this light, notice IR (Identifier Restoration): it crushes the other transformations by giving 30% code reduction. This shows that JavaScript’s scope is complex: by this metric 30% of JavaScript’s complexity is due to its scope.
Takeaway
These semantics-altering transformations give semantic restrictions on JS. Our paper makes these restrictions precise. And they’re exactly the sorts of simplifying assumptions that papers need to make to reason about JS. You can even download λs5 from git and implement your analysis over λs5 with a subset of these restrictions turned on, and test it. So let’s work toward a future where papers that talk about JS say exactly what sub-language of JS they mean.
The Paper
This is just a teaser: to read more, see the paper.
Tierless Programming for SDNs: Differential Analysis
Tags: Flowlog, Programming Languages, Software-Defined Networking, Verification
Posted on 02 June 2015.
This post is part of our series about tierless network programming with Flowlog:
Part 1: Tierless Programming
Part 2: Interfacing with External Events
Part 3: Optimality
Part 4: Verification
Part 5: Differential Analysis
Verification is a powerful way to make sure a program meets expectations, but what if those expectations aren't written down, or the user lacks the expertise to write formal properties? Flowlog supports a powerful form of property-free analysis: program differencing.
When we make a program change, usually we're starting from a version that "works". We'd like to transfer what confidence we had in the original version to the new version, plus confirm our intuition about the changes. In other words, even if the original program had bugs, we'd like to at least confirm that the edit doesn't introduce any new ones.
Of course, taking the syntactic difference of two programs is easy — just use diff! — but usually that's not good enough. What we want is the behavioral, or semantic difference. Flowlog provides semantic differencing via Alloy, similarly to how it does property checking. We call Flowlog's differencing engine Chimp (short for Change-impact).
Differences in Output and State Transitions
Chimp translates both the old (prog1) and new (prog2) versions to Alloy, then supports asking questions like: Will the two versions ever handle packets differently? More generally, we can ask Chimp whether the program's output behavior ever differs: does there exist some program state and input event such that, in that state, the two programs will disagree on output?
pred changePolicyOut[st: State, ev: Event] {
some out: Event |
prog1/outpolicy[st,ev,out] && not prog2/outpolicy[st,ev,out] ||
prog2/outpolicy[st,ev,out] && not prog1/outpolicy[st,ev,out]
}
Any time one program issues an output event that the other doesn't, Chimp
displays an Alloy scenario.
We might also ask: When can the programs change state differently? Similarly to changePolicyOut above, Chimp defines changeStateTransition[st: State, ev: Event] as matching any of the following for each table T in the program:
some x0, ..., xn: univ |
prog1/afterEvent_T[prestate, ev, x0, ..., xn] &&
not prog2/afterEvent_T[prestate, ev, x0, ..., xn] ||
prog2/afterEvent_T[prestate, ev, x0, ..., xn] &&
not prog1/afterEvent_T[prestate, ev, x0, ..., xn]
Recall that afterEvent_T keeps track of when each tuple is in the table T after an event is processed.
Refining Differential Analysis
The two predicates above are both built into Chimp. Using them as a starting point, users can ask pointed questions about the effects of the change. For instance, will any TCP packets be handled differently? Just search for a pre-state and a TCP packet that the programs disagree on:
some prestate: State, p: EVtcp_acket | changePolicyOut[prestate, p]This lets users explore the consequences of their change without any formal guidance except their intuition about what the change should do.
Reachability
So far, these queries show scenarios where the programs differ, taking into consideration all potential inputs and starting states; this includes potentially unreachable starting states. We could, for instance, have two programs that behave differently if a table is populated (resulting in a non-empty semantic diff!) yet never actually insert rows into that table. Chimp provides optional reachability-checking to counter this, although users must cap the length of system traces being searched.
Schema Clashes
Suppose that we want to modify the original source-tracking example to keep track of flows by source and destination, rather than just source addresses. Now instead of one column:
TABLE seen(macaddr);the seen table has two columns:
TABLE seen(macaddr, macaddr);
This poses a challenge for Chimp; what shape should the seen table be? If Chimp finds a scenario, should it show a seen table with one or two columns? We call this situation a schema clash, and Chimp addresses it by creating two separate tables in the prestate: one with one column (used by the first program) and another with two columns (used by the second program).
Doing this causes a new issue: Chimp searches for arbitrary states that satisfy the change-impact predicates. Since there is no constraint between the values of the two tables, Chimp might return a scenario where (say) the first seen table is empty, but the second contains tuples!
This doesn't match our intuition for the change: we expect that for every source in the first table, there is a source-destination pair in the second table, and vice versa. We can add this constraint to Chimp and filter the scenarios it shows us, but first, we should ask whether that constraint actually reflects the behavior of the two programs.
Differential Properties
Since it's based on Flowlog's verification framework, Chimp allows us to check properties stated over multiple programs. Our expecation above, stated in Alloy for an arbitrary state s, is:
all src: Macaddr | src in s.seen1 iff some dst: Macaddr | src->dst in s.seen2
Let's check that this condition holds for all reachable states. We'll proceed inductively. The condition holds trivially at the starting (empty) state; so we only need to show that it is preserved as the program transitions. We search for a counterexample:
some prestate: State, ev: Event | {
// prestate satisfies the condition
all src: Macaddr | src in prestate.seen_1 iff
some dst: Macaddr | src->dst in prestate.seen_2
// poststate does not
some src: Macaddr |
(prog1/afterEvent_seen_1[prestate,ev,src] and
all dst: Macaddr | not prog2/afterEvent_seen_2[prestate,ev,src,dst])
||
(not prog1/afterEvent_seen_1[prestate,ev,src] and
some dst: Macaddr | prog2/afterEvent_seen_2[prestate,ev,src,dst])
}
Chimp finds no counterexample. Unfortunately, Chimp can't guarantee that this isn't a false negative; the query falls outside the class where Chimp can guarantee a complete search. Nevertheless, the lack of counterexample serves to increase our confidence that the change respects our intent.
After adding the constraint that, for every source in the first table, there is a source-destination pair in the second table, Chimp shows us that the new program will change the state (to add a new destination) even if the source is already in seen.
Further Reading
Chimp supports more features than discussed here; for instance, Chimp can compare the behavior of any number of program versions, but a two-program comparison is the most common. You can read more about Chimp in our paper.
Tierless Programming for SDNs: Verification
Tags: Flowlog, Programming Languages, Software-Defined Networking, Verification
Posted on 17 April 2015.
This post is part of our series about tierless network programming with Flowlog:
Part 1: Tierless Programming
Part 2: Interfacing with External Events
Part 3: Optimality
Part 4: Verification
Part 5: Differential Analysis
The last post said what it means for Flowlog's compiler to be optimal, which prevents certain bugs from ever occurring. But what about the program itself? Flowlog has built-in features to help verify program correctness, independent of how the network is set up.
To see Flowlog's program analysis in action, let's first expand our watchlist program a bit more. Before, we just flooded packets for demo purposes:
DO forward(new) WHERE
new.locPt != p.locPt;
Now we'll do something a bit smarter. We'll make the program learn which ports
lead to which hosts, and use that knowledge to avoid flooding when possible (this
is often called a "learning switch"):
TABLE learned(switchid, portid, macaddr);
ON packet(pkt):
INSERT (pkt.locSw, pkt.locPt, pkt.dlSrc) INTO learned;
DO forward(new) WHERE
learned(pkt.locSw, new.locPt, pkt.dlDst);
OR
(NOT learned(pkt.locSw, ANY, pkt.dlDst) AND
pkt.locPt != new.locPt);
The learned table stores knowledge about where addresses have been
seen on the network. If a packet arrives with a destination the switch has
seen before as a source, there's no need to flood! While this program is still
fairly naive (it will fail if the network has cycles in it) it's complex
enough to have a few interesting properties we'd like to check. For instance,
if the learned table ever holds multiple ports for the same switch
and address, the program will end up sending multiple copies of the same
packet. But can the program ever end up in such a state? Since the initial,
startup state is empty, this amounts to checking:
Verifying Flowlog
Each Flowlog rule defines part of an event-handling function saying how the system should react to each packet seen. Rules compile to logical implications that Flowlog's runtime interprets whenever a packet arrives.
Alloy is a tool for analyzing relational logic specifications. Since Flowlog rules compile to logic, it's easy to describe in Alloy how Flowlog programs behave. In fact, Flowlog can automatically generate Alloy specifications that describe when and how the program takes actions or changes its state.For example, omitting some Alloy-language foibles for clarity, here's how Flowlog describes our program's forwarding behavior in Alloy.
pred forward[st: State, p: EVpacket, new: EVpacket] {
// Case 1: known destination
(p.locSw->new.locPt->p.dlDst) in learned and
(p.locSw->new.locPt) in switchHasPort and ...)
or
// Case 2: unknown destination
(all apt: Portid | (p.locSw->apt->p.dlDst) not in learned and
new.locPt != p.locPt and
(p.locSw->new.locPt) in switchHasPort and ...)
}
An Alloy predicate is either true or false for a given input. This one says
whether, in a given state st, an arbitrary packet p will be
forwarded as a new packet new (containing the output port and any
header modifications).
It combines both forwarding rules together to construct a logical definition
of forwarding behavior, rather than just a one-way implication (as in the case
of individual rules).
The automatically generated specification also contains other predicates that say how and when the controller's state will change. For instance, afterEvent_learned, which says when a given entry will be present in learned after the controller processes a packet. An afterEvent predicate is automatically defined for every state table in the program.
Using afterEvent_Learned, we can verify our goal: that whenever an event ev arrives, the program will never add a second entry (sw, pt2,addr) to learned:
assert FunctionalLearned {
all pre: State, ev: Event |
all sw: Switchid, addr: Macaddr, pt1, pt2: Portid |
(not (sw->pt1->addr in pre.learned) or
not (sw->pt2->addr in pre.learned)) and
afterEvent_learned[pre, ev, sw, pt1, addr] and
afterEvent_learned[pre, ev, sw, pt2, addr] implies pt1 = pt2
}
Alloy finds a counterexample scenario (in under a second):
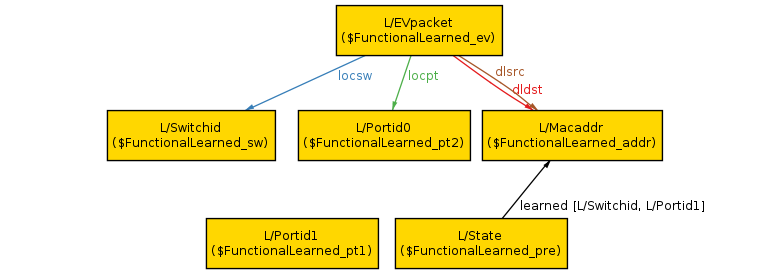
The scenario shows an arbitrary packet (L/EVpacket; the L/ prefix can be ignored) arriving at port 1 (L/Portid1) on an arbitrary switch (L/Switchid). The packet has the same source and destination MAC address (L/Macaddr). Before the packet arrived, the controller state had a single row in its learned table; it had previously learned that L/Macaddr can be reached out port 0 (L/Portid1). Since the packet is from the same address, but a different port, it will cause the controller to add a second row to its learned table, violating our property.
This situation isn't unusual if hosts are mobile, like laptops on a campus network are. To fix this issue, we add a rule that removes obsolete mappings from the table:
DELETE (pkt.locSw, pt, pkt.dlSrc) FROM learned WHERE not pt = pkt.locPt;Alloy confirms that the property holds of the modified program. We now know that any reachable state of our program is valid.
Verification Completeness
Alloy does bounded verification: along with properties to check, we provide concrete bounds for each datatype. We might say to check up to to 3 switches, 4 IP addresses, and so on. So although Alloy never returns a false positive, it can in general produce false negatives, because it searches for counterexamples only up to the given bounds. Fortunately, for many useful properties, we can compute and assert a sufficient bound. In the property we checked above, a counterexample needs only 1 State (to represent the program's pre-state) and 1 Event (the arriving packet), plus room for its contents (2 Macaddrs for source and destination, etc.), along with 1 Switchid, 2 Portids and 1 Macaddr to cover the possibly-conflicted entries in the state. So when Alloy says that the new program satisfies our property, we can trust it.
Benefits of Tierlessness
Suppose we enhanced the POX version of this program (Part 1) to learn ports in the same way, and then wanted to check the same property. Since the POX program explicitly manages flow-table rules, and the property involves a mixture of packet-handling (what is sent up to the controller?) and controller logic (how is the state updated?), checking the POX program would mean accounting for those rules and how the controller updates them over time. This isn't necessary for the Flowlog version, because rule updates are all handled optimally by the runtime. This means that property checking is simpler: there's no multi-tiered model of rule updates, just a model of the program's behavior.
You can read more about Flowlog's analysis support in our paper.
In the next post, we'll finish up this sequence on Flowlog by reasoning about behavioral differences between multiple versions of the same program.
Tierless Programming for SDNs: Optimality
Tags: Flowlog, Programming Languages, Software-Defined Networking, Verification
Posted on 13 April 2015.
This post is part of our series about tierless network programming with Flowlog:
Part 1: Tierless Programming
Part 2: Interfacing with External Events
Part 3: Optimality
Part 4: Verification
Part 5: Differential Analysis
Since packets can trigger controller-state updates and event output, you might wonder exactly which packets a Flowlog controller needs to see. For instance, a packet without a source in the watchlist will never alter the controller's state. Does such a packet need to grace the controller at all? The answer is no. In fact, there are only three conditions under which switch rules do not suffice, and the controller must be involved in packet-handling:
- when the packet will cause a change in controller state;
- when the packet will cause the controller to send an event; and
- when the packet must be modified in ways that OpenFlow 1.0 does not support on switches.
Flowlog's compiler ensures the controller sees packets if and only if one of these holds; the compiler is therefore optimal with respect to this list. To achieve this, the compiler analyzes every packet-triggered statement in the program. For instance, the INSERT statement above will only change the state for packets with a source in the watchlist (a condition made explicit in the WHERE clause) and without a source in the seen table (implicit in Flowlog's logical semantics for INSERT). Only if both of these conditions are met will the controller see a packet. An optimal compiler prevents certain kinds of bugs from occurring: the controller program will never miss packets that will affect its state, and it will never receive packets it doesn't need.
You can read more about Flowlog in our paper.
In the next post, we'll look at Flowlog's built-in verification support.
Tierless Programming for SDNs: Events
Tags: Flowlog, Programming Languages, Software-Defined Networking, Verification
Posted on 01 March 2015.
This post is part of our series about tierless network programming with Flowlog:
Part 1: Tierless Programming
Part 2: Interfacing with External Events
Part 3: Optimality
Part 4: Verification
Part 5: Differential Analysis
The last post introduced Flowlog, a tierless language for SDN controller programming. You might be wondering, "What can I write in Flowlog? How expressive is it?" To support both its proactive compiler and automated program analysis (more on this in the next post) we deliberately limited Flowlog's expressive power. There are no loops in the language, and no recursion. Instead of trying to be universally expressive, Flowlog embraces the fact that most programs don't run in a vacuum. A controller may need to interact with other services, and developers may wish to re-use pre-existing code. To enable this, Flowlog programs can call out to non-Flowlog libraries. The runtime uses standard RPCs (Thrift) for inter-process communication, so existing programs can be quickly wrapped to communicate with Flowlog. Much like how Flowlog abstracts out switch-rule updates, it also hides the details of inter-process communcation. To see this, let's enhance the address-logger application with a watch-list that external programs can add to. We need a new table ("watchlist"), populated by arriving "watchplease" events that populate the table. Finally, we make sure only watched addresses are logged:
TABLE seen(macaddr);
TABLE watchlist(macaddr);
EVENT watchplease = {target: macaddr};
ON watchplease(w):
INSERT (w.target) INTO watchlist;
ON packet(p):
INSERT (p.dlSrc) INTO seen WHERE
watchlist(p.dlSrc);
DO forward(new) WHERE
new.locPt != p.locPt;
When the program receives a watchplease event (sent via RPC from an external
program) it adds the appropriate address to its watchlist.
Sending Events
Flowlog programs can also send events. Suppose we want to notify some other process when a watchlisted address is seen, and the process is listening on TCP port 20000. We just declare a named pipe that carries notifications to that port:
EVENT sawaddress = {addr: macaddr};
OUTGOING sendaddress(sawaddress) THEN
SEND TO 127.0.0.1:20000;
and then write a notification to that pipe for appropriate packets:
ON packet(p) WHERE watchlist(p.dlSrc): DO sendaddress(s) WHERE s.addr = p.dlSrc;
Synchronous Communication
The event system supports asynchronous communication, but Flowlog also allows synchronous queries to external programs. It does this with a remote state abstraction. If we wanted to manage the watchlist remotely, rather than writingTABLE watchlist(macaddr);we would write:
REMOTE TABLE watchlist(macaddr) FROM watchlist AT 127.0.0.1 20000 TIMEOUT 10 seconds;which tells Flowlog it can obtain the current list by sending queries to port 20000. Since these queries are managed behind the scenes, the program doesn't need to change—as far as the programmer is concerned, a table is a table. Finally, the timeout says that Flowlog can cache prior results for 10 seconds.
Interfacing External Programs with Flowlog
Flowlog can interface with code in any language that supports Thrift RPC (including C++, Java, OCaml, and many others). To interact with Flowlog, one only needs to implement the interface Flowlog requires: a function that accepts notifications and a function that responds to queries. Other functions may also (optionally) send notifications. Thrift's library handles the rest.You can read more about Flowlog's events in our paper.
In the next post, we'll look at what it means for Flowlog's compiler to be optimal.
Tierless Programming for Software-Defined Networks
Tags: Flowlog, Programming Languages, Software-Defined Networking, Verification
Posted on 30 September 2014.
This post is part of our series about tierless network programming with Flowlog:
Part 1: Tierless Programming
Part 2: Interfacing with External Events
Part 3: Optimality
Part 4: Verification
Part 5: Differential Analysis
Network devices like switches and routers update their behavior in real-time. For instance, a router may change how it forwards traffic to address an outage or congestion. In a traditional network, devices use distributed protocols to decide on mutually consistent behavior, but Software-Defined Networks (SDN) operate differently. Switches are no longer fully autonomous agents, but instead receive instructions from logically centralized controller applications running on separate hardware. Since these applications can be arbitrary programs, SDN operators gain tremendous flexibility in customizing their network.
The most popular SDN standard in current use is OpenFlow. With OpenFlow, Controller applications install persistent forwarding rules on the switches that match on packet header fields and list actions to take on a match. These actions can include header modifications, forwarding, and even sending packets to the controller for further evaluation. When a packet arrives without a matching rule installed, the switch defaults to sending the packet to the controller for instructions.
Let's write a small controller application. It should (1) record the addresses of machines sending packets on the network and (2) cause each switch to forward traffic by flooding (i.e., sending out on all ports except the arrival port). This is simple enough to write in POX, a controller platform for Python. The core of this program is a function that reacts to packets as they arrive at the controller (we have removed some boilerplate and initialization):
def _handle_PacketIn (self, event):
packet = event.parsed
def install_nomore ():
msg = of.ofp_flow_mod()
msg.match = of.ofp_match(dl_src = packet.src)
msg.buffer_id = event.ofp.buffer_id
msg.actions.append(of.ofp_action_output(port = of.OFPP_FLOOD))
self.connection.send(msg)
def do_flood ():
msg = of.ofp_packet_out()
msg.actions.append(of.ofp_action_output(port = of.OFPP_FLOOD))
msg.data = event.ofp
msg.buffer_id = None
msg.in_port = event.port
self.connection.send(msg)
self.seenTable.add(packet.src)
install_nomore()
do_flood()
First, the controller records the packet's source in its internal table. Next, the install_nomore function adds a rule to the switch saying that packets with this source should be flooded. Once the rule is installed, the switch will not send packets with the same source to the controller again. Finally, the do_flood function sends a reply telling the switch to flood the packet.
This style of programming may remind you of the standard three-tier web-programming architecture. Much like a web program generates JavaScript or SQL strings, controller programs produce new switch rules in real-time. One major difference is that switch rules are much less expressive than JavaScript, which means that less computation can be delegated to the switches. A bug in a controller program can throw the entire network's behavior off. But it's easy to introduce bugs when every program produces switch rules in real-time, effectively requiring its own mini-compiler!
SDN Programming Without Tiers
We've been working on a tierless language for SDN controllers: Flowlog. In Flowlog, you write programs as if the controller sees every packet, and never have to worry about the underlying switch rules. This means that some common bugs in controller/switch interaction can never occur, but it also means that the programming experience is simpler. In Flowlog, our single-switch address-monitoring program is just:
TABLE seen(macaddr); ON ip_packet(p): INSERT (p.dlSrc) INTO seen; DO forward(new) WHERE new.locPt != p.locPt;
The first line declares a one-column database table, "seen". Line 2 says that the following two lines are triggered by IP packets. Line 3 adds those packets' source addresses to the table, and line 4 sends the packets out all other ports.
As soon as this program runs, the Flowlog runtime proactively installs switch rules to match the current controller state and automatically ensures consistency. As the controller sees more addresses, the switch sends fewer packets back to the controller—but this is entirely transparent to the programmer, whose job is simplified by the abstraction of an all-seeing controller.
Examples and Further Reading
Flowlog is good for more than just toy examples. We've used Flowlog for many different network applications: ARP-caching, network address translation, and even mediating discovery and content-streaming for devices like Apple TVs. You can read more about Flowlog and Flowlog applications in our paper.
The next post talks more about what you can use Flowlog to write, and also see how Flowlog allows programs to call out to external libraries in other languages.
Verifying Extensions’ Compliance with Firefox's Private Browsing Mode
Tags: Browsers, JavaScript, Programming Languages, Security, Verification, Types
Posted on 19 August 2013.All modern browsers now support a “private browsing mode”, in which the browser ostensibly leaves behind no traces on the user's file system of the user's browsing session. This is quite subtle: browsers have to handle caches, cookies, preferences, bookmarks, deliberately downloaded files, and more. So browser vendors have invested considerable engineering effort to ensure they have implemented it correctly.
Firefox, however, supports extensions, which allow third party code to run with all the privilege of the browser itself. What happens to the security guarantee of private browsing mode, then?
The current approach
Currently, Mozilla curates the collection of extensions, and any extension must pass through a manual code review to flag potentially privacy-violating behaviors. This is a daunting and tedious task. Firefox contains well over 1,400 APIs, of which about twenty are obviously relevant to private-browsing mode, and another forty or so are less obviously relevant. (It depends heavily on exactly what we mean by the privacy guarantee of “no traces left behind”: surely the browser should not leave files in its cache, but should it let users explicitly download and save a file? What about adding or deleting bookmarks?) And, if the APIs or definition of private-browsing policy ever change, this audit must be redone for each of the thousands of extensions.
The asymmetry in this situation should be obvious: Mozilla auditors should not have to reconstruct how each extension works; it should be the extension developers' responsibility to convince the auditor that their code complies with private-browsing guarantees. After all, they wrote the code! Moreover, since auditors are fallible people, too, we should look to (semi-)automated tools to lower their reviewing effort.
Our approach
So what property, ultimately, do we need to confirm about an extension's code to ensure its compliance? Consider the pseudo-code below, which saves the current preferences to disk every few minutes:
var prefsObj = ...
const thePrefsFile = "...";
function autoSavePreferences() {
if (inPivateBrowsingMode()) {
// ...must store data only in memory...
return;
} else {
// ...allowed to save data to disk...
var file = openFile(thePrefsFile);
file.write(prefsObj.tostring());
}
}
window.setTimeout(autoSafePreferences, 3000);The key observation is that this code really defines two programs that happen to share the same source code: one program runs when the browser is in private browsing mode, and the other runs when it isn't. And we simply do not care about one of those programs, because extensions can do whatever they'd like when not in private-browsing mode. So all we have to do is “disentangle” the two programs somehow, and confirm that the private-browsing version does not contain any file I/O.
Technical insight
Our tool of choice for this purpose is a type system for JavaScript. We've used such a system before to analyze the security of the ADsafe sandbox. The type system is quite sophisticated to handle JavaScript idioms precisely, but for our purposes here we need only part of its expressive power. We need three pieces: first, three new types; second, specialized typing rules; and third, an appropriate type environment.
- We define one new primitive type:
Unsafe. We will ascribe this type to all the privacy-relevant APIs. - We use union types to define
Ext, the type of “all private-browsing-safe extensions”, namely: numbers, strings, booleans, objects whose fields areExt, and functions whose argument and return types areExt. Notice thatUnsafe“doesn’t fit” intoExt, so attempting to use an unsafe function, or pass it around in extension code, will result in a type error. - Instead of defining
Boolas a primitive type, we will instead defineTrueandFalseas primitive types, and defineBoolas their union.
- If an expression has some union type, and only one component
of that union actually typechecks, then we optimistically say
that the expression typechecks even with the whole union type.
This might seem very strange at first glance: surely, the
expression
5("true")shouldn't typecheck? But remember, our goal is to prevent privacy violations, and the code above will simply crash---it will never write to disk. Accordingly, we permit this code in our type system. - We add special rules for typechecking if-expressions. When
the condition typechecks at type
True, we only check the then-branch; when the condition typechecks at typeFalse, we only check the else-branch. (Otherwise, we check both branches as normal.)
- We give all the privacy-relevant APIs the
type
Unsafe. - We give the API
inPrivateBrowsingMode()the typeTrue. Remember: we just don't care what happens when it's false!
Put together, what do all these pieces achieve?
Because Unsafe and Ext are disjoint from
each other, we can safely segregate any code into two pieces that
cannot communicate with each other. By carefully initializing the
type environment, we make Unsafe precisely delineate
the APIs that extensions should not use in private browsing mode.
The typing rules for if-expressions plus the type
for inPrivateBrowsingMode() amount to disentangling the
two programs from each other: essentially, it implements dead-code
elimination at type-checking time. Lastly, the rule about union
types makes the system much easier for programmers to use, since they
do not have to spend any effort satisfying the typechecker about
properties other than this privacy guarantee.
In short, if a program passes our typechecker, then it must not call any privacy-violating APIs while in private-browsing mode, and hence is safe. No audit needed!
Wait, what about exceptions to the policy?
Sometimes, extensions have good reasons for writing to disk even
while in private-browsing mode. Perhaps they're updating their
anti-phishing blacklists, or they implement a download-helper that
saves a file the user asked for, or they are a bookmark manager. In
such cases, there simply is no way for the code to typecheck. As in
any type system, we provide a mechanism to break out of the type
system: an unchecked typecast. We currently write such casts
as cheat(T). Such casts must be checked by a human
auditor: they are explicitly marking the places where the extension
is doing something unusual that must be confirmed.
(In our original version, we took our cue from Haskell and wrote
such casts as unsafePerformReview, but sadly that is
tediously long to write.)
But does it work?
Yes.
We manually analyzed a dozen Firefox extensions that had already
passed Mozilla's auditing process. We annotated the extensions with
as few type annotations as possible, with the goal of forcing the
code to pass the typechecker, cheating if necessary.
These annotations found five extensions that violated
the private-browsing policy: they could not be typechecked without
using cheat, and the unavoidable uses
of cheat pointed directly to where the extensions
violated the policy.
Further reading
We've written up our full system, with more formal definitions of the types and worked examples of the annotations needed. The writeup also explains how we create the type environment in more detail, and what work is necessary to adapt this system to changes in the APIs or private-browsing implementation.
From MOOC Students to Researchers
Tags: Education, Programming Languages, Semantics
Posted on 18 June 2013.Much has been written about MOOCs, including the potential for its users to be treated, in effect, as research subjects: with tens of thousands of users, patterns in their behavior will stand out starkly with statistical significance. Much less has been written about using MOOC participants as researchers themselves. This is the experiment we ran last fall, successfully.
Our goal was to construct a “tested semantics” for Python, a popular programming language. This requires some explanation. A semantics is a formal description of the behavior of a language so that, given any program, a user can precisely predict what the program is going to do. A “tested” semantics is one that is validated by checking it against real implementations of the language itself (such as the ones that run on your computer).
Constructing a tested semantics requires covering all of a large language, carefully translating its every detail into a small core language. Sometimes, a feature can be difficult to translate. Usually, this just requires additional quantities of patience, creativity, or elbow grease; in rare instances, it may require extending the core language. Doing this for a whole real-world language is thus a back-breaking effort.
Our group has had some success building such semantics for multiple languages and systems. In particular, our semantics for JavaScript has come to be used widely. The degree of interest and rapidity of uptake of that work made clear that there was interest in this style of semantics for other languages, too. Python, which is not only popular but also large and complex (much more so than JavaScript), therefore seemed like an obvious next target. However, whereas the first JavaScript effort (for version 3 of the language) took a few months for a PhD student and an undergrad, the second one (focusing primarily on the strict-mode of version 5) took far more effort (a post-doc, two PhD students, and a master's student). JavaScript 5 approaches, but still doesn't match, the complexity of Python. So the degree of resources we would need seemed daunting.
Crowdsourcing such an effort through, say, Mechanical Turk did not seem very feasible (though we encourage someone else to try!). Rather, we needed a trained workforce with some familiarity with the activity of formally defining a programming language. In some sense, Duolingo has a similar problem: to be able to translate documents it needs people who know languages. Duolingo addresses it by...teaching languages! In a similar vein, our MOOC on programming languages was going to serve the same purpose. The MOOC would deliver a large and talented workforce; if we could motivate them, we could then harness them to help perform the research.
During the semester, we therefore gave three assignments to get students warmed up on Python: 1, 2, and 3. By the end of these three assignments, all students in the class had had some experience wrestling with the behavior of a real (and messy) programming language, writing a definitional interpreter for its core, desugaring the language to this core, and testing this desugaring against (excerpts of) real test suites. The set of features was chosen carefully to be both representative and attainable within the time of the course.
(To be clear, we didn't assign these projects only because we were interested in building a Python semantics. We felt there would be genuine value for our students in wrestling with these assignments. In retrospect, however, this was too much work, and it interfered with other pedagogic aspects of the course. As a result, we're planning to shift this workload to a separate, half-course on implementing languages.)
Once the semester was over, we were ready for the real business to begin. Based on the final solutions, we invited several students (out of a much larger population of talent) to participate in taking the project from this toy sub-language to the whole Python language. We eventually ended up with an equal number of people who were Brown students and who were from outside Brown. The three Brown students were undergraduates; the three outsiders were an undergraduate student, a professional programmer, and a retired IT professional who now does triathlons. The three outsiders were from Argentina, China, and India. The project was overseen by a Brown CS PhD student.
Even with this talented workforce, and the prior preparation done through the course and creating the assignments prepared for the course, getting the semantics to a reasonable state was a daunting task. It is clear to us that it would have been impossible to produce an equivalent quality artifact—or to even come close—without this many people participating. As such, we feel our strategy of using the MOOC was vindicated. The resulting paper has just been accepted at a prestigious venue that was the most appropriate one for this kind of work, with eight authors: the lead PhD student, the three Brown undergrads, the three non-Brown people, and the professor.
A natural question is whether making the team even larger would have helped. As we know from Fred Brooks's classic The Mythical Man Month, adding people to projects can often hurt rather than help. Therefore, the determinant is to what extent the work can be truly parallelized. Creating a tested semantics, as we did, has a fair bit of parallelism, but we may have been reaching its limits. Other tasks that have previously been crowdsourced—such as looking for stellar phenomena or trying to fold proteins—are, as the colloquial phrase has it, “embarrassingly parallel”. Most real research problems are unlikely to have this property.
In short, the participants of a MOOC don't only need to be thought of as passive students. With the right training and motivation, they can become equal members of a distributed research group, one that might even have staying power over time. Also, participation in such a project can help a person establish their research abilities even when they are at some remove from a research center. Indeed, the foreign undergraduate in our project will be coming to Brown as a master's student in the fall!
Would we do it again? For this fall, we discussed repeating the experiment, and indeed considered ways of restructuring the course to better support this goal. But before we do, we have decided to try to use machine learning instead. Once again, machines may put people out of work.
(Sub)Typing First Class Field Names
Tags: Programming Languages, Semantics, Types
Posted on 10 December 2012.This post picks up where a previous post left off, and jumps back into the action with subtyping.
Updating Subtyping
There are two traditional rules for subtyping records, historically known as width and depth subtyping. Width subtyping allows generalization by dropping fields; one record is a supertype of another if it contains a subset of the sub-record's fields at the same types. Depth subtyping allows generalization within a field; one record is a supertype of another if it is identical aside from generalizing one field to a supertype of the type in the same field in the sub-record.
We would like to understand both of these kinds of subtyping in the context of our first-class field names. With traditional record types, fields are either mentioned in the record or not. Thus, for each possible field in both types, there are four combinations to consider. We can describe width and depth subtyping in a table:
T1 |
T2 |
T1 <: T2 if... |
|---|---|---|
f: S |
f: T |
S <: T |
f: - |
f: T |
Never |
f: S |
f: - |
Always |
f: - |
f: - |
Always |
We read f: S as saying that T1 has
the field f with type S, and we read f:
- as saying that the corresponding type doesn't mention the field
f. The first row of the table corresponds to
depth subtyping, where the field f is still
present, but at a more general type in T2. The
second row is a failure to subtype, when T2 has
a field that isn't mentioned at all in T1. The
third row corresponds to width subtyping, where a field is
dropped and not mentioned in the supertype. The last row is a trivial
case, where neither type mentions the field.
For records with string patterns, we can extend this table with new combinations to account for ○ and ↓ annotations. The old rows remain, and become the ↓ cases, and new rows are added for ○ annotations:
T1 |
T2 |
T1 <: T2 if... |
|---|---|---|
f↓: S |
f↓: T |
S <: T |
f○: S |
f↓: T |
Never |
f: - |
f↓: T |
Never |
f↓: S |
f○: T |
S <: T |
f○: S |
f○: T |
S <: T |
f: - |
f○: T |
Never |
f↓: S |
f: - |
Always |
f○: S |
f: - |
Always |
f: - |
f: - |
Always |
Here, we see that it is safe to treat a definitely present field as a
possibly-present one, in the case where we compare
f↓:S to f○:T). The dual
of this case, treating a possibly-present field as definitely-present,
is unsafe, as the comparison of f○:S to
f↓:T shows. Possibly present annotations do not
allow us to invent fields, as having f: - on the
left-hand-side is still only permissible if the right-hand-side also
doesn't mention f.
Giving Types to Values
In order to ascribe these rich types to object values, we need rules for typing basic objects, and then we need to apply these subtyping rules to generalize them. As a working example, one place where objects with field patterns come up every day in practice is in JavaScript arrays. Arrays in JavaScript hold their elements in fields named by stringified numbers. Thus, a simplified type for a JavaScript array of booleans is roughly:
BoolArrayFull: { [0-9]+○: Bool }
That is, each field made up of a sequence of digits is possibly present, and if it is there, it has a boolean value. For simplicity, let's consider a slightly neutered version of this type, where only single digit fields are allowed:
BoolArray: { [0-9]○: Bool }
Let's think about how we'd go about typing a value that should
clearly have this type: the array [true, false]. We can
think of this array literal as desugaring into an object like (indeed,
this is what λJS
does):
{"0": true, "1": false}We would like to be able to state that this object is a member of the
BoolArray type above. The traditional rule for record
typing would ascribe a type mapping the names that are present to the
types of their right hand side. Since the fields are certainly present,
in our notation we can write:
{"0"↓: Bool, "1"↓: Bool}
This type should certainly be generalizable to
BoolArray. That is, it should hold (using the rules in the
table above) that:
{"0"↓: Bool, "1"↓: Bool} <: { [0-9]○: Bool }
Let's see what happens when we instantiate the table for these two types:
T1 |
T2 |
T1 <: T2 if... |
|---|---|---|
0↓: Bool |
0○: Bool |
Bool <: Bool |
1↓: Bool |
1○: Bool |
Bool <: Bool |
3: - |
3○: Bool |
Fail! |
4: - |
4○: Bool |
Fail! |
| ... | ... | ... |
(We cut off the table for 5-9, which are the same as the cases for 3 and 4). Our subtyping fails to hold for these types, which don't let us reflect the fact that the fields 3 and 4 are actually absent, and we should be allowed to consider them as possibly present at the boolean type. In fact, our straightforward rule for typing records is in fact responsible for throwing away this information! The type that it ascribed,
{"0"↓: Bool, "1"↓: Bool}
is actually the type of many objects, including those that happen to
have fields like "banana" : 42. Traditional record typing
drops fields when it doesn't care if they are present or absent, which
loses information about definitive absence.
We extend our type language once more to keep track of this information. We add an explicit piece of a record type that tracks a description of the fields that are definitely absent on an object, and use this for typing object literals:
p = ○ | ↓
T = ... | { Lp : T ..., LA: abs }
Thus, the new type for ["0": true, "1": false] would be:
{"0"↓: Bool, "1"↓: Bool, ("0"|"1"): abs}
Here, the overbar denotes
regular-expression complement, and this type is expressing that all
fields other than "0" and "1" are definitely
absent.
Adding another type of field annotation requires that we again extend our table of subtyping options, so we now have a complete description with 16 cases:
T1 |
T2 |
T1 <: T2 if... |
|---|---|---|
f↓: S |
f↓: T |
S <: T |
f○: S |
f↓: T |
Never |
f: abs |
f↓: T |
Never |
f: - |
f↓: T |
Never |
f↓: S |
f○: T |
S <: T |
f○: S |
f○: T |
S <: T |
f: abs |
f○: T |
Always |
f: - |
f○: T |
Never |
f↓: S |
f: abs |
Never |
f○: S |
f: abs |
Never |
f: abs |
f: abs |
Always |
f: - |
f: abs |
Never |
f↓: S |
f: - |
Always |
f○: S |
f: - |
Always |
f: abs |
f: - |
Always |
f: - |
f: - |
Always |
We see that absent fields cannot be generalized to be definitely present
(the abs to f↓ case), but
they can be generalized to be possibly present at any type.
This is expressed in the case that compares f : abs
to f○: T, which always holds for any
T. To see these rules in action, we can instantiate them
for the array example we've been working with to ask a new question:
{"0"↓: Bool, "1"↓: Bool, ("0"|"1"): abs} <: { [0-9]○: Bool }
And the table:
T1 |
T2 |
T1 <: T2 if... |
|---|---|---|
0↓: Bool |
0○: Bool |
Bool <: Bool |
1↓: Bool |
1○: Bool |
Bool <: Bool |
3: abs |
3○: Bool |
OK! |
4: abs |
4○: Bool |
OK! |
| ... | ... | ... |
9: abs |
9○: Bool |
OK! |
foo: abs |
foo: - |
OK! |
bar: abs |
bar: - |
OK! |
| ... | ... | ... |
There's two things that make this possible. First, it is sound to generalize the absent fields that are possibly present on the array type, because the larger type doesn't guarantee their presence either. Second, it is sound to generalize absent fields that aren't mentioned on the array type, because unmentioned fields can be present or absent with any type. The combination of these two features of our subtyping relation lets us generalize from particular array instances to the more general type for arrays.
Capturing the Whole Table
The tables above present subtyping on a field-by-field basis, and the patterns we considered at first were finite. In the last case, however, the pattern of “fields other than 0 and 1” was in fact infinite, and we cannot actually construct that infinite table to describe subtyping. The writeup and its associated proof document lay out an algorithmic version of the rules presented in the tables above, and also provides a proof of their soundness.
The writeup also discusses another interesting problem, which is the
interaction between these pattern types and inheritance, where patterns
on the child and parent objects may overlap in subtle ways. It goes
further and discusses what happens in cases like JavaScript, where the
field "__proto__" is an accessible member that has
inheritance semantics. Check it all out here!
Typing First Class Field Names
Tags: Programming Languages, Semantics, Types
Posted on 03 December 2012.In a previous post, we discussed some of the powerful features of objects in scripting languages. One feature that stood out was the use of first-class strings as member names for objects. That is, in programs like
var o = {name: "Bob", age: 22};
function lookup(f) {
return o[f];
}
lookup("name");
lookup("age"); the name position in field lookup has been abstracted over.
Presumably only a finite set of names actually works with the lookup
(o appears to only have two fields, after all).
It turns out that so-called “scripting” languages aren't the only
ones that compute fields for lookup. For example, even within the
constraints of Java's type system, the Bean framework computes method
names to call at runtime. Developers can provide information about the
names of fields and methods on a Bean with a BeanInfo
instance, but even if they don't provide complete information, “the rest
will be obtained by automatic analysis using low-level reflection of the
bean classes’ methods and applying standard design patterns.” These
“standard design patterns” include, for example, concatenating the
strings "get" and "set" onto field names to
produce method names to invoke at runtime.
Traditional type systems for objects and records have little to say about these computed accesses. In this post, we're going to build up a description of object types that can describe these values, and explore their use. The ideas in this post are developed more fully in a writeup for the FOOL Workshop.
First-class Singleton Strings
In the JavaScript example above, we said that it's likely that the only
intended lookup targets―and thus the only intended arguments to
lookup―are "name" and "age".
Giving a meaningful type to this function is easy if we allow singleton
strings as types in their own right. That is, if our type language is:
T = s | Str | Num
| { s : T ... } | T → T | T ∩ T
Where s stands for any singleton string, Str
and Num are base types for strings and numbers,
respectively, record types are a map from singleton strings
s to types, arrow types are traditional pairs of types, and
intersections are allowed to express a conjunction of types on the same
value.
Given these definitions, we could write the type of lookup as:
lookup : ("name" → Str) ∩ ("age" → Num)
That is, if lookup is provided the string
"name", it produces a string, and if it is provided the
string "age", it produces a number.
In order to type-check the body of lookup, we need a
type for o as well. That can be represented with the type
{ "name" : Str, "age" : Num }. Finally, to type-check the
object lookup expression o[f], we need to compare the
singleton string type of f with the fields of
o. In this case, only the two strings that are already
present on o are possible choices for f, so
the comparison is easy and type-checking works out.
For a first cut, all we did was make the string labels on objects'
fields a first-class entity in our type system, with singleton string
types s. But what can we say about the Bean example, where
get* and set* method invocations are computed
rather than just used as first-class values?
String Pattern Types
In order to express the type of objects like Beans, we need to express
field name patterns, rather than just singleton field names.
For example, we might say that a Bean with Int-typed
parameters has a type like:
IntBean = { ("get".+) : → Int },
("set".+) : Int → Void,
"toString" : → Str }
Here, we are using .+ as regular expression notation
for any non-empty string. We read the type above as saying that all
fields that begin with get and end with any string are
functions that return Int values. The same is true for
"set" methods. The singleton string "toString"
is also a field, and is simply a function that returns strings.
To express this type, we need to extend our type language to handle these string patterns, which we write down as regular expressions (the write-up outlines the actual limits on what kinds of patterns we can support). We extend our type language to include patterns as types, and as field names:
L = regular expressions
T = L | Str | Num
| { L : T ... } | T → T | T ∩ T
This new specification gives us the ability to write down types like
IntBean, which have field patterns that describe
infinite sets of fields. Let's stop and think about what that
means as a description of a runtime object. Our type for o
above, { "name" : Str, "age" : Num }, says that values
bound to o at runtime certainly have name and
age fields at the listed types. The type for
IntBean, on the other hand, seems to assert that these
objects will have the fields getUp, getDown,
getSerious, and infinitely more. But a runtime object
can't actually have all of those fields, so a pattern
indicating an infinite number of field names is describing a
fundamentally different kind of value.
What an object type with an infinite pattern represents is that all the fields that match the pattern are potentially present. That is, at runtime, they may or may not be there, but if they are there, they must have the annotated type. We extend object types again to make this explicit with presence annotations, which explicitly list fields as definitely present, written ↓, or possibly present, written ○:
p = ○ | ↓
T = ... | { Lp : T ... }
In this notation, we would write:
IntBean = { ("get".+)○ : → Int },
("set".+)○ : Int → Void,
"toString"↓ : → Str }
Which indicates that all the fields in ("get".+) and
("set".+) are possibly present with the given
arrow types, and toString is definitely present.
Subtyping
Now that we have these rich object types, it's natural to ask what kinds of subtyping relationships they have with one another. A detailed account of subtyping will come soon; in the meantime, can you guess what subtyping might look like for these types?
Update: The answer is in the next post.
S5: Engineering Eval
Tags: JavaScript, Programming Languages, Semantics
Posted on 21 October 2012.In an earlier post, we introduced S5, our semantics for ECMAScript 5.1 (ES5). S5 is no toy, but strives to correctly model JavaScript's messy details.
One such messy detail of JavaScript is eval. The
behavior of eval was updated in the ES5 specification to
make its behavior less surprising and give more control to programmers.
However, the old behavior was left intact for backwards compatibility.
This has led to a language construct with a number of subtle behaviors.
Today, we're going to explore JavaScript's eval, explain
its several modes, and describe our approach to engineering an
implementation of it.
Quiz Time!
We've put together a short quiz to give you a tour of the various
types of eval in JavaScript. How many can you get right on
the first try?
Question 1
function f(x) {
eval("var x = 2;");
return x;
}
f(1) === ?;
f(1) === 2
This example returns 2 because the var declaration in
the eval actually refers to the same variables as
the body of the function. So, the eval body overwrites the
x parameter and returns the new value.
Question 2
function f(x) {
eval("'use strict'; var x = 2;");
return x;
}
f(1) === ?;
f(1) === 1
The 'use strict'; directive creates a new scope for
variables defined inside the eval. So, the
var x = 2; still evaluates, but doesn't affect the
x that is the function's parameter. These first two
examples show that strict mode
changes the scope that eval affects. We might
ask, now that we've seen these, what scope does eval
see?
Question 3
function f(x) {
eval("var x = y;");
return x;
}
f(1) === ?;
f(1) === ReferenceError: y is not defined
OK, that was sort of a trick question. This program throws an
exception saying that y is unbound. But it serves to
remind us of an important JavaScript feature; if a variable isn't
defined in a scope, trying to access it is an exception. Now we can ask
the obvious question: can we see y if we define it outside
the eval?
Question 4
function f(x) {
var y = 2;
eval("var x = y;");
return x;
}
f(1) === ?;
f(1) === 2
OK, here's our real answer. The y is certainly visible
inside the eval, which can both see and affect the outer
scope. What if the eval is strict?
Question 5
function f(x) {
var y = 2;
eval("'use strict'; var x = y;");
return x;
}
f(1) === ?;
f(1) === 1
Interestingly, we don't get an error here, so
it seems like y was visible to the eval
even in strict mode. However, as before the assignment doesn't
escape. New topic next.
Question 6
function f(x) {
var avel = eval;
avel("var x = y;");
return x;
}
f(1) === ?;
f(1) === ReferenceError: y is not defined
OK, that was a gimme. Lets add the variable declaration we need.
Question 7
function f(x) {
var avel = eval;
var y = 2;
avel("var x = y;");
return x;
}
f(1) === ?;
f(1) --> ReferenceError: y is not defined
What's going on here? We defined a variable and it isn't visible
like it was before, and all we did was rename eval.
Let's try a simpler example.
Question 8
function f(x) {
var avel = eval;
avel("var x = 2;");
return x;
}
f(1) === ?;
f(1) === 1
OK, so somehow we aren't seeing the assignment to x
either... Let's try making one more observation:
Question 9
function f(x) {
var avel = eval;
avel("var x = 2;");
return x;
}
f(1);
x === ?;
x === 2
Whoa! So that eval changed the x in the global
scope. This is what the specification refers to as an
indirect eval; when the call to eval doesn't
use a direct reference to the variable eval.
Question 10 (On the home stretch!)
function f(x) {
"use strict";
eval("var x = 2;");
return x;
}
f(1) === ?;
x === ?;
f(1) === 1
Before, when we had "use strict"; inside the
eval, we saw that the variable declarations did not
escape. Here, the "use strict"; is outside, but we see
the same thing: the value of
1 simply flows through to the return statement
unaffected. Second, we know that we aren't doing the same thing as
the indirect eval from the previous question,
because we didn't affect the global scope.
Question 11 (last one!)
function f(x) {
"use strict";
var avel = eval;
avel("var x = 2;");
return x;
}
f(1) === ?;
x === ?;
f(1) === 1
x === 2
Unlike in the previous question, this indirect eval has
the same behavior as before: it affects the global scope. The
presence of a "use strict"; appears to mean something different to an
indirect versus a direct eval.
Capturing all the Evals
We saw three factors that could affect the behavior of eval
above:
-
Whether the code passed to
evalwas instrictmode; -
Whether the code surrounding the
evalwas instrictmode; and -
Whether the
evalwas direct or indirect.
Each of these is a binary choice, so there are eight potential
configurations for an eval. Each of the eight cases
specifies both:
-
Whether the
evalsees the current scope or the global one; -
Whether variables introduced in the
evalare seen outside of it.
We can crisply describe all of these choices in a table:
| Strict outside? | Strict inside? | Direct or Indirect? | Local or global scope? | Affects scope? |
|---|---|---|---|---|
| Yes | Yes | Indirect | Global | No |
| No | Yes | Indirect | Global | No |
| Yes | No | Indirect | Global | Yes |
| No | No | Indirect | Global | Yes |
| Yes | Yes | Direct | Local | No |
| No | Yes | Direct | Local | No |
| Yes | No | Direct | Local | No |
| No | No | Direct | Local | Yes |
Rows where eval can affect some scope are shown in red
(where it cannot is blue),
and rows where the string passed to eval is strict mode code are in
bold.
Some patterns emerge here that make some of the design decisions of
eval clear. For example:
- If the
evalis indirect it always uses global scope; if direct it always uses local scope. - If the string passed to
evalis strict mode code, then variable declarations will not be seen outside theeval. - An indirect
evalbehaves the same regardless of the strictness of its context, while directevalis sensitive to it.
Engineering eval
To specify eval, we need to somehow both detect these
different configurations, and evaluate code with the right combination
of visible environment and effects. To do so, we start with a flexible
primitive that lets us evaluate code in an environment expressed as an
object:
internal-eval(string, env-object)
This internal-eval expects env-object to be an
object whose fields represent the environment to evaluate in. No
identifiers other than those in the passed-in environment are bound.
For example, a call like:
internal-eval("x + y", { "x" : 2, "y" : 5 })
Would evaluate to 7, using the values of the
"x" and "y" fields from the environment object as the
bindings for the identifiers x and y. With
this core primitive, we have the control we need to implement all the
different versions of eval.
In previous
posts, we talked about the
overall strategy of our evaluator for JavaScript. The relevant
high-level point for this discussion is that we define a core language,
dubbed S5, that contains only the essential features of JavaScript.
Then, we define a source-to-source transformer, called desugar,
that converts JavaScript programs to S5 programs. Since our evaluator
is defined only over S5, we need to use desugar in our
interpreter to perform the evaluation step. Semantically, the
evaluation of internal-eval is then:
internal-eval(string, env-object) -> desugar(string)[x1 / v1, ...] for each x1 : v1 in env-object (where [x / v] indicates substitution)
It is the combination of desugar and the customizable
environment argument to internal-eval that let us implement
all of JavaScript's eval forms. We actually
desugar all calls to JavaScript's eval into a
function call defined in S5 called maybeDirectEval, which
performs all the necessary checks to construct the correct environment
for the eval.
Leveraging S5's Eval
With our implementation of eval, we have made progress on a
few fronts.
Analyzing more JavaScript: We can now tackle more programs
than any of our prior formal semantics for JavaScript. For example, we
can actually run all of the complicated evals in
Secure ECMAScript, and
print the
heap inside a use of a sandboxed eval. This enables
new kinds of analyses that we haven't been able to perform before.
Understanding scripting languages' eval: Other
scripting languages, like Ruby and Python, also have eval.
Their implementations are closer to our internal-eval, in
that they take dictionary arguments that specify the bindings that are
available inside the evaluation. Is something like
internal-eval, which was inspired by well-known semantic
considerations, a useful underlying mechanism to use to describe all of
these?
The implementation of S5 is open-source, and a detailed report of our strategy and test results is appearing at the Dynamic Languages Symposium. Check them out if you'd like to learn more!
Progressive Types
Tags: Programming Languages, Semantics, Types
Posted on 01 September 2012.Adding types to untyped languages has been studied extensively, and with good reason. Type systems offer developers strong static guarantees about the behavior of their programs, and adding types to untyped code allows developers to reap these benefits without having to rewrite their entire code base. However, these guarantees come at a cost. Retrofitting types on to untyped code can be an onerous and time-consuming process. In order to mitigate this cost, researchers have developed methods to type partial programs or sections of programs, or to allow looser guarantees from the type system. (Gradual typing and soft typing are some examples.) This reduces the up-front cost of typing a program.
However, these approaches only address a part of the problem. Even if the programmer is willing to expend the effort to type the program, he still cannot control what counts as an acceptable program; that is determined by the type system. This significantly reduces the flexibility of the language and forces the programmer to work within a very strict framework. To demonstrate this, observe the following program in Racket...
#lang racket (define (gt2 x y) (> x y))
...and its Typed Racket counterpart.
#lang typed/racket (: gt2 (Number Number -> Boolean)) (define (gt2 x y) (> x y))
The typed example above, which appears to be logically typed, fails to type-check. This is due to the sophistication with which Typed Racket handles numbers. It can distinguish between complex numbers and real numbers, integers and non-integers, even positive and negative integers. In this system, Number is actually an alias for Complex. This makes sense in that complex numbers are in fact the super type of all other numbers. However, it would also be reasonable to assume that Number means Real, because that's what people tend to think of when they think “number”. Because of this, a developer may expect all functions over real numbers to work over Numbers. However, this is not the case. Greater-than, which is defined over reals, cannot be used with Number because it is not defined over complex numbers. Now, this could be resolved by changing the type of gt2 to take Reals, rather than Numbers. But then consider this program:
#lang typed/racket (: plus (Number Number -> Number)) (define (plus x y) (+ x y)) ;Looks fine so far... (: gt2 (Real Real -> Boolean)) (define (gt2 x y) (> x y)) ;...Still ok... (gt2 (plus 3 4) 5) ;...Here (plus 3 4) evaluates to a Number which causes gt2 to give ;the type error “Expected Real but got Complex”.Now, in order to make this program type, we would have to adjust plus to return Reals, even though it works with it's current typing! And we'd have to do the same for every program that calls plus. This can cause a ripple effect through the program, making typing the program labor-intensive, despite the fact that the program will actually run just fine on some inputs, which may be all we care about. But we still have to jump through hoops to get the program to run at all!
In the above example, the type system in Typed Racket requires the programmer to ensure that there are no runtime errors caused by using a complex number where a real number is expected, even if it means significant extra programming effort. There are cases, however, where type systems do not provide guarantees because it would cross the threshold of too much work for programmers. One such guarantee is ensuring that vector references are always given positive integer inputs. The Typed Racket type system does not offer this guarantee because of the required programming effort, and so it traded that particular guarantee for convenience and ease of programming.
In both these cases, type systems are trying to determine the best balance betwen safety and convenience. However, the best a system can do is choose either safety or convenience and apply that to all programs. Vector references cannot be checked in any program, because it isn't worth the extra engineering effort, whereas all programs must be checked for number realness, because it's worth the extra engineering effort. This seems pretty arbirtary! Type systems are trying to guess at what the developer might want, instead of just asking. However, the developer has a much better idea of which checks are relevant and important for a specific program and which are irrelevant or unimportant. The type system should leverage this information and offer the useful guarantees without requiring unhelpful ones.
Progressive Types
To this end, we have developed progressive types, which allow the developer to require type guarantees that are significant to the program, and ignore those that are irrelevant. From the total set of possible type errors, the developer would select which among them must be detected as compile time type errors, and which should be allowed to possibly cause runtime failures. In the above example, the developer could allow errors caused by treating a Number as a Real at runtime, trusting that they will never occur or that it won't be catastrophic if they do or that the particular error is orthogonal to the reasons for type-checking the program at all. Thus, the developer can disregard an insignificant error while still reaping the benefits of the rest of the type system. This addresses a problem that underlies all type systems: The programmer doesn't get to choose which classes of programs are “good” and which are “bad.” Progressive types give the programmer that control.
In order to allow this, the type system has an allowed error set, Ω, in addition to the type environment. So while a traditional typing rule takes the form Γ⊢e:τ, a rule in progressive type would take the form Ω;Γ⊢e:τ. Here, Ω is the set of errors the developer wants to allow to cause runtime failures. Expressions may evaluate to errors, and if those errors are in Ω, the expression will type to ⊥, otherwise it will fail to type. This is reflected in the progress theorem that goes along with the type system.
If Typed Racket were a progressively typed language, the above program would type only if the programmer had selected “Expected Real, but got Complex” to be in Ω. This means that if numerical calculations are really orthogonal to the point of the program, or there are other checks in place insuring the function will only get the right type of input, the developer can just tell the type checker not to worry about those errors! However, if it's important to ensure that complex numbers never appear where reals are required, the developer can tell the type checker to detect those errors. Thus the programmer can determine what constitutes a “good” program, rather than working around a different, possibly inconvenient, definition of “good”. By passing this control over to the developer, progressive type systems allow the balance between ease of engineering and saftey to be set at a level appropriate to the program.
Progressive typing differs from gradual typing in that while gradual typing allows the developer to type portions of a program with a fixed type system, progressive types instead allow the developer to vary the guarantees offered by the type system. Further, like soft typing, progressive typing allows for runtime errors instead of static guarantees, but unlike soft typing, it restricts which classes of runtime failures are allowed to occur. Because our system allows programmers to progressively adjust the restrictions imposed by the type system, either to loosen or tighten them, they can reap many of the flexibility benefits of a dynamic languages, but get static guarantees of a type system in the way best suited to each of their programs or preferences.
If you are interested in learning more about progressive types, look here.
Mechanized LambdaJS
Tags: JavaScript, Programming Languages, Semantics
Posted on 04 June 2012.See the discussion on Lambda the Ultimate about this work.
In an earlier post, we introduced λJS, our operational semantics for JavaScript. Unlike many other operational semantics, λJS is no toy, but strives to correctly model JavaScript's messy details. To validate these claims, we test λJS with randomly generated tests and with portions of the Mozilla JavaScript test suite.
Testing is not enough. Despite our work, other researchers found a missing case in λJS. Today, we're introducing Mechanized λJS, which comes with a machine-checked proof of correctness, using the Coq proof assistant.
Recap: The Structure of λJS
λJS has two key parts: an operational semantics and a desugaring function. Our earlier post discusses how we tackle the minutiae of JavaScript with our desugaring function. This post focuses on the operational semantics, where others found a bug, which now has a machine-checked proof of correctness.
The operational semantics is typical of programming languages research. It specifies the sequence of steps required to evaluate the program. For example, the following sequence evaluates to a value:
{ x: 2 + 3, y : 9 }["x"] * (11 + 23)
→ { x: 5, y: 9 }["x"] * (11 + 23)
→ 5 * (11 + 23)
→ 5 * 34
→ 170
The sequence above evaluates expressions from left to right—a detail
spelled out in the operational semantics.
Not all expressions reduce to values. For example, the following reduces to an error:
null["x"] → err "Cannot read property 'x' of null"An operational semantics specifies exactly which errors may occur.
Finally, an operational semantics allows some programs to run forever. This is a basic infinite loop, and its non-terminating reduction sequence:
while (true) { 1; }
→ if true then 1; while (true) { 1; } else undefined
→ 1; while (true) { 1; }
→ while (true) { 1; }
→ if true then 1; while (true) { 1; } else undefined
→ 1; while (true) { 1; }
…
In general, these are the only three cases that the semantics should allow—an expression must either (1) evaluate to a value, (2) signal an error, or (3) not terminate. In fact, we can state that as a theorem.
Theorem 1 (Soundness). For all λJS programs, p, either:
- p →* v,
- p →* err, or
- p →* p2, and there exists a p3 such that p2 → p3.
This is a standard theorem worth proving for any language. Since languages and their correctness proofs involve detailed, delicate designs and decisions, the proofs are easy to do wrong, and tedious for humans to get right. If only computers could help.
PLT Redex: Lightweight Mechanization
We first developed λJS in PLT Redex, a domain-specific language embedded in Racket for specifying operational semantics.
Redex brings dull semantics to life. It doesn't just make a semantics executable, but also lets you visualize it. For example, here is our first example sequence in Redex (parentheses included):
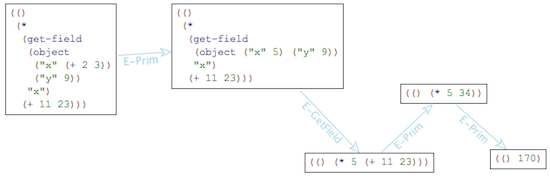
The visualizer is a lot of fun, and a very effective debugging tool. It helped us catch several bugs in the early design of λJS.
Redex can also generate random tests to exercise your semantics. Random testing caught several more bugs in λJS.
Coq: A Machine-Checked Proof
Testing is not enough. We shipped λJS with a bug that breaks the soundness theorem above. We didn't discover it for a year. David van Horn and Ian Zerny both reported it to us independently. We'd missed a case in the semantics, which caused certain terms to get "stuck". It turned out to be a simple fix, but we were left wondering if anything else was left lurking.
To gain further assurance, we mechanized λJS with the Coq proof assistant. The soundness theorem now has a machine-checked proof of correctness. You still need to read the Coq definition of λJS and ensure it matches your intuitions. But once that's done, you can be confident that the proofs are valid.
Doing this proof was surprisingly easy, once we'd read Software Foundations and Certified Programming with Dependent Types. We'd like to thank Benjamin Pierce and his co-authors, and Adam Chlipala, for putting their books online.
What's Done
Here's what we've got so far:
- A PLT Redex model,
- A Coq model, and
- A proof of soundness in Coq.
What's Next
We're not done. Here's what's coming up:
- There are a few easy bits missing from the Coq model (e.g., a parameterized delta-function).
- Once those easy bits are done, we'll wire it together with desugaring.
- Finally, we'll upgrade the model to support semantics for ECMAScript 5.
Objects in Scripting Languages
Tags: JavaScript, Programming Languages, Semantics
Posted on 28 February 2012.We've been studying scripting languages in some detail, and have collected a number features of their object systems that we find unusually expressive. This expressiveness can be quite powerful, but also challenges attempts to reason about and understand programs that use these features. This post outlines some of these exceptionally expressive features for those who may not be intimately familiar with them.
Dictionaries with Inheritance
Untyped scripting languages implement objects as dictionaries mapping member names (strings) to values. Inheritance affects member lookup, but does not affect updates and deletion. This won't suprise any experienced JavaScript programmer:
var parent = {"z": 9};
// Using __proto__ sets up inheritance directly in most browsers
var obj = { "x": 1, "__proto__": parent};
obj.x // evaluates to 1
obj.z // evaluates to 9
obj.z = 50 // creates new field on obj
obj.z // evaluates to 50, z on parent is "overridden"
parent.z // evaluates to 9; parent.z was unaffected by obj.z = 50In other scripting languages, setting up this inheritance can't be done quite so directly. Still, its effect can be accomplished, and the similar object structure observed. For example, in Python:
class parent(object):
z = 9 # class member
def __init__(self):
self.x = 1 # instance member
obj = parent()
obj.x # evaluates to 1
obj.z # evaluates to 9
obj.z = 50 # creates new field on obj
obj.z # evaluates to 50, z on parent is "overridden"
parent.z # evaluates to 9, just like JavaScript We can delete the field in both languages, which returns
obj to its original state, before it was extended with a
z member. In JavaScript:
delete obj.z;
obj.z // evaluates to 9 againThis also works in Python:
delattr(obj, "z");
obj.z # evaluates to 9 againIn both languages, we could have performed the assignments and lookups with computed strings as well:
// JavaScript
obj["x " + "yz"] = 99 // creates a new field, "x yz"
obj["x y" + "z"] // evaluates to 99# Python
setattr(obj, "x " + "yz", 99) # creates a new field, "x yz"
getattr(obj, "x y" + "z") # evaluates to 99We can go through this entire progression in Ruby, as well:
class Parent; def z; return 9; end; end
obj = Parent.new
class << obj; def x; return 1; end; end
obj.x # returns 1
obj.z # returns 9
class << obj; def z; return 50; end; end
obj.z # return 50
# no simple way to invoke shadowed z method
class << obj; remove_method :z; end
obj.z # returns 9
class << obj
define_method("xyz".to_sym) do; return 99; end
end
print obj.xyz # returns 99Classes Do Not Shape Objects
The upshot is that a class definition in a scripting language says little about the structure of its instances. This is in contrast to a language like Java, in which objects' structure is completely determined by their class, to the point where memory layouts can be predetermined for runtime objects. In scripting languages, this isn't the case. An object is an instance of a 'class' in JavaScript, Python, or Ruby merely by virtue of several references to other runtime objects. Some of these be changed at runtime, others cannot, but in all cases, members can be added to and removed from the inheriting objects. This flexibility can lead to some unusual situations.
Brittle inheritance: Fluid classes make inheritance brittle. If we start with this Ruby class:
class A
def initialize; @privateFld = 90; end
def myMethod; return @privateFld * @privateFld; end
end Then we might assume that implementation of myMethod assumes
a numeric type for @privateFld. This assumption can be
broken by subclasses, however:
class B < A
def initialize; super(); @privateFld = "string (not num)"; end
end
Since both A and B use the same name, and it
is simply a dictionary key, B instances violate the
assumptions of A's methods:
obj = B.new
B.myMethod # error: cannot multiply stringsRuby's authors are well aware of this; the Ruby manual states "it is only safe to extend Ruby classes when you are familiar with (and in control of) the implementation of the superclass" (page 240).
Mutable Inheritance: JavaScript and Python expose the
inheritance chain through mutable object members. In JavaScript, we
already saw that the member "__proto__" could be used to
implement inheritance directly. The "__proto__" member is
mutable, so class hierarchies can be changed at runtime. We found it a
bit more surprising when we realized the same was possible in Python:
class A(object):
def method(self): return "from class A"
class B(object):
def method(self): return "from class B"
obj = A()
obj.method() # evaluates to "from class A"
isinstance(obj, A) # evaluates to True
obj.__class__ = B # the __class__ member determines inheritance
obj.method() # evaluates to "from class B"
isinstance(obj, B) # evaluates to True: obj's 'class' has changed!Methods?
These scripting languages also have flexible, and different, definitions of "methods".
JavaScript simply does not have methods. The syntax
obj.method(...)
Binds this to the value of obj in the body of
method. However, the method member is just a
function and can be easily extracted and applied:
var f = obj.method; f(...);
Since f() does not use the method call syntax above, it is
treated as a function call. In this case, it is a well known JavaScript
wart that this is bound to a default "global object" rather
than obj.
Python and Ruby make a greater effort to retain a binding for the
this parameter. Python doesn't care about the name of the
parameter (though self is canonically used), and simply has
special semantics for the first argument of a method. If a method is
extracted via member access, it returns a function that binds the object
from the member access to the first parameter:
class A(object):
def __init__(self_in_init): self_in_init.myField = 900
def method(self_in_method): return self_in_method.myField
obj = A()
f1 = obj.method # the access binds self_in_method to obj
f1() # evaluates to 900, using the above bindingIf the same method is accessed as a field multiple times, it isn't the same function both times―a new function is created for each access:
obj = A()
f1 = obj.method # first extraction
f2 = obj.method # second extraction
f1 is f2 # evaluates to False, no reference equality
Python lets programmers access the underlying function without the first
parameter bound through the member im_func. This is
actually the same reference across all extracted methods, regardless of
even the original object of extraction:
obj = A()
f1 = obj.method # first extraction
f2 = obj.method # second extraction
otherobj = A()
f3 = obj.method # extraction from another object
# evaluates to True, same function referenced from extractions on the
# same object
f1.im_func is f2.im_func
# evaluates to True, same function referenced from extractions on
# different objects
f2.im_func is f3.im_funcRuby has a similar treatment of methods, their extraction, and their reapplication to new arguments.
But Why?
These features aren't just curiosities―we've found examples where they are used in practice. For example, Django's ORM builds classes dynamically, modifying them based on strings that come from modules describing database tables and relationships ( base.py):
attr_name = '%s_ptr' % base._meta.module_name
field = OneToOneField(base, name=attr_name,
auto_created=True, parent_link=True)
new_class.add_to_class(attr_name, field)Ruby on Rails' ActiveRecord uses dynamic field names as well, iterating over fields and invoking methods only when their names match certain patterns ( base.rb):
attributes.each do |k, v|
if k.include?("(")
multi_parameter_attributes << [ k, v]
elsif respond_to?("#{k}=")
if v.is_a?(Hash)
nested_parameter_attributes << [ k, v ]
else
send("#{k}=", v)
else
raise(UnkownAttributeError, "unknown attribute: #{k}")
end
endThese applications use objects as dictionaries (with inheritance) to build up APIs that they couldn't otherwise.
These expressive features aren't
without their perils. Django has
explicit warnings that things can go awry if relationships between
tables expressed in ORM classes overlap. And the fact that
__proto__ is in the same namespace as the other members bit
Google Docs, whose
editor would crash if the string "__proto__" was
entered. The implementation was using an object as a hashtable keyed by
strings from the document, which led to an assignment to
__proto__ that changed the behavior of the map.
So?
The languages presented here are widely adopted and used, and run critical systems. Yet, they contain features that defy conventional formal reasoning, at the very least in their object systems. Perhaps these features' expressiveness outweighs the cognitive load of using them. If it doesn't, and using these features is too difficult or error-prone, we should build tools to help us use them, or find better ways to implement the same functionality. And if not, we should take notice and recall that we have these powerful techniques at our disposal in the next object system we design.
S5: Wat?
Tags: JavaScript, Programming Languages, Semantics
Posted on 31 January 2012.Gary Bernhardt's Wat talk has been making a well-deserved round of the blogodome in the past few weeks. If you haven't seen it, go give it a watch (you can count it as work time, since you saw it on the Brown PLT Blog, and we're Serious Researchers). The upshot of the second half of the talk is that JavaScript has some less than expected behaviors. We happen to have a JavaScript implementation floating around in the form of S5, and like to claim that it handles the hairy corners of the language. We decided to throw Gary's examples at it.
The Innocuous +
Gary's first JavaScript example went like this:
failbowl:~(master!?) $ jsc
> [] + []
> [] + {}
[object Object]
> {} + []
0
> {} + {}
NaN S5 lacks a true REPL―it simply takes JavaScript strings and produces
output and answers―so we started by approximating a little bit. We
first tried a series of print statements to see if we got
the same effect:
$ cat unit-tests/wat-arrays.js
print([] + []);
print([] + {});
print({} + []);
print({} + {});
$ ./s5 < unit-tests/wat-arrays.js
[object Object]
[object Object]
[object Object][object Object]
undefinedWAT.
Well, that doesn't seem good at all. Only half of the answers are
right, and there's an undefined at the end. What went
wrong? It turns out the semantics of REPLs are to blame. If we take
the four programs and run them on their own, we get something that looks
quite a bit better:
$ ./s5 "[] + []"
""
$ ./s5 "[] + {}"
"[object Object]"
$ ./s5 "{} + []"
0.
$ ./s5 "{} + {}"
nanThere are two issues here:
- Why do
0.andnanprint like that? - Why did this work, when the previous attempt didn't?
The answer to the first question is pretty straightforward: under the covers, S5 is using Ocaml floats and printing Ocaml values at the end of its computation, and Ocaml makes slightly different decisions than JavaScript in printing numbers. We could change S5 to print answers in JavaScript-printing mode, but the values themselves are the right ones.
The second question is more interesting. Why do we get such different answers depending on whether we evaluate individual strings versus printing the expressions? The answer is in the semantics of JavaScript REPLs. When parsing a piece of JavaScript, the REPL needs to make a choice. Sensible decisions would be to treat each new JavaScript string as a Statement, or as an entire JavaScript Program. Most REPLs choose the Program production.
The upshot is that the parsing of {} + {} is quite
different from [] + []. With S5, it's trivial to print the
desugared representation and understand the difference. When we parse
and desugar, we get very different results for {} + {} and
[] + []:
$ ./s5-print "{} + {}"
{undefined;
%UnaryPlus({[#proto: %ObjectProto,
#class: "Object",
#extensible: true,]
})}
$ ./s5-print "[] + []"
%PrimAdd({
[#proto: %ArrayProto,
#class: "Array",
#extensible: true,]
'length' : {#value 0., #writable true, #configurable false}
},
{
[#proto: %ArrayProto,
#class: "Array",
#extensible: true,]
'length' : {#value 0., #writable true, #configurable false}
}
)
It is clear that {} + {} parses as two statements (an
undefined followed by a UnaryPlus), and
[] + [] as a single statement containing a binary addition
expression. What's happening is that in the Program production, for the
string {} + {}, the first {} is matched with
the Block
syntactic form, with no internal statements. The rest of the expression
is parsed as a UnaryExpression. This is in
contrast to [] + [], which only correctly parses as an
ExpressionStatement containing an AdditiveExpression.
In the example where we used successive print
statements, every expression in the argument position to print
was parsed in the second way, hence the different answers. The lesson?
When you're at a REPL, be it Firebug, Chrome, or the command line, make
sure the expression you're typing is what you think it is: not being
aware of this difference can make it even more difficult to know what to
expect!
If You Can't Beat 'Em...
Our first example led us on an interesting excursion into parsing,
from which S5 emerged triumphant, correctly modelling the richness
and/or weirdness of the addition examples. Next up, Gary showed some
straightforward uses of Array.join():
failbowl:~(master!?) $ jsc
> Array(16)
,,,,,,,,,,,,,,,,
> Array(16).join("wat")
watwatwatwatwatwatwatwatwatwatwatwatwatwatwatwat
> Array(16).join("wat" + 1)
wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1
> Array(16).join("wat" - 1) + " Batman"
NaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaN Batman Our results look oh-so-promising, right up until the last line
(note: we call String on the first case, because S5 doesn't
automatically toString answers, which the REPL does).
$ ./s5 "String(Array(16))"
",,,,,,,,,,,,,,,,"
$ ./s5 "Array(16).join('wat')"
"watwatwatwatwatwatwatwatwatwatwatwatwatwatwatwat"
$ ./s5 "Array(16).join('wat' + 1)"
"wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1wat1"
$ ./s5 "Array(16).join('wat' - 1) + ' Batman'"
"nullnullnullnullnullnullnullnullnullnullnullnullnullnullnullnull Batman"WAT.
Are we really that awful that we somehow yield null rather
than NaN? A quick glance at the desugared code shows us
that we actually have the constant value null as
the argument to join(). How did that happen?
Interestingly, the following version of the program works:
$ ./s5 "var wat = 'wat'; Array(16).join(wat - 1) + ' Batman';"
"NaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaN Batman" This leads us to our answer. We use SpiderMonkey's very handy Parser
API as part of our toolchain. Reflect.parse() takes
strings and converts them to JSON structures with rich AST information,
which we stringify and pass off to the innards of S5 to do desugaring
and evaluation. Reflect.parse() is part of a JavaScript
implementation that strives for performance, and to that end it performs
constant folding. That is, as an optimization, when it sees the
expression "wat" - 1, it automatically converts it to
NaN. All good so far.
The issue is that the NaN yielded by constant folding
is not quite the same NaN we might expect in JavaScript
programs. In JavaScript, the identifier NaN is a
property of the global object with the value
NaN. The Parser API can't safely fold to the
identifier NaN (as was pointed
out to us when we reported this bug), because it might be shadowed
in a different context. Presumably to avoid this pitfall, the folding
yields a JSON structure that looks like:
expression:{type:"Literal", value:NaN} But we can't sensibly use JSON.stringify() on this
structure, because NaN isn't valid JSON! Any guesses on
what SpiderMonkey's JSON implementation turns NaN into? If
you guessed null, we owe you a cookie.
We have designed a
hack based on suggestions from the bug report to get around this
(passing a function to stringify to look for
NaNs and return a stylized object literal instead).
There's a bug open to make constant folding optional in
Reflect.parse(), so this will be fixed in Mozilla's
parser. (Update) The bug
is fixed, and we've updated our version of Spidermonkey. This example
now works happily, thanks to Dave Herman.
Producing a working JavaScript implementation leads to a whole host of exciting moments and surprising discoveries. Building this semantics and its desugaring gives us much more confidence that our tools say something meaningful about real JavaScript programs. These examples show that getting perfect correspondence is difficult, but we strive to be as close as possible.
S5: Semantics for Accessors
Tags: JavaScript, Programming Languages, Semantics
Posted on 11 December 2011.Getters and setters (known as accessors) are a new feature in ECMAScript 5 that extend the behavior of assignment and lookup expressions on JavaScript objects. If a field has a getter defined on it, rather than simply returning the value in field lookup, a getter function is invoked, and its return value is the result of the lookup:
var timesGotten = 0;
var o = {get x() { timesGotten++; return 22; }};
o.x; // calls the function above, evaluates to 22
timesGotten; // is now 1, due to the increment in the getter
o.x; // calls the function above, still evaluates to 22
timesGotten; // is now 2, due to another increment in the getterSimilarly, if a field has a setter defined on it, the setter function is called on field update. The setter function gets the assigned value as its only argument, and its return value is ignored:
var foo = 0;
var o = {set x(v) { foo = v; }};
o.x = 37; // calls the function above (with v=37)
foo; // evaluates to 37
o.x; // evaluates to undefined Getters and setters have a number of proposed uses―they can be used to wrap
DOM objects that have interesting effects on assignment, like
onmessage and onbeforeunload, for example. We leave
discovering good uses to more creative JavaScript programmers, and focus on
their semantic properties here.
The examples above are straightforward, and it seems like a simple model might work out quite easily. First, we need some definitions, so we'll start with what's in λJS. Here's a fragment of the values that λJS works with, and the most basic of the operations on objects:
v := str | { str1:v1, ⋯, strn:vn } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | e(e, ⋯) | ⋯
(E-Lookup)
{ ⋯, str:v, ⋯ }[strx] → v
when strx = str
(E-Update)
{ ⋯, str:v, ⋯}[strx=v'] → { ⋯, str:v', ⋯}
when strx = str
(E-UpdateAdd)
{ str1:v1, ⋯}[str=v] → { str:v, str1:v1, ⋯}
when str ≠ str1, ⋯
We update and set fields when they are found, and add fields if there is an update on a not-found field. Clearly, this isn't enough to model the semantics of getters and setters. On lookup, if the value of a field is a getter, we need to have our semantics step to an invocation of the function. We need to make the notion of a field richer, so the semantics can have behavior that depends on the kind of field. We distinguish two kinds of fields p, one for simple values and one for accessors:
p := [get: vg, set: vs] | [value: v]
v := str | { str1:p1, ⋯, strn:pn } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | e(e, ⋯) | ⋯
The updated rules for simple values are trivial to write down (differences in bold):
(E-Lookup)
{ ⋯, str:[value:v], ⋯ }[strx] → v
when strx = str
(E-Update)
{ ⋯, str:[value:v], ⋯}[strx=v'] → { ⋯, str:[value:v'], ⋯}
when strx = str
(E-UpdateAdd)
{ str1:v1, ⋯}[str=v] → { str:[value:v], str1:v1, ⋯}
when str ≠ str1, ⋯
But now we can also handle the cases where we have a getter or setter. If a lookup expression e[e] finds a getter, it applies the function, and the same goes for setters, which get the value as an argument:
(E-LookupGetter)
{ ⋯, str:[get:vg, set:vs], ⋯ }[strx] → vg()
when strx = str
(E-UpdateSetter)
{ ⋯, str:[get:vg, set:vs], ⋯}[strx=v'] → vs(v')
when strx = str
Great! This can handle the two examples from the beginning of the post. But those two examples weren't the whole story for getters and setters, and our first fragment wasn't the whole story for λJS objects.
Consider this program:
var o = {
get x() { return this._x + 1; },
set x(v) { this._x = v * 2; }
};
o.x = 5; // calls the set function above (with v=5)
o._x; // evaluates to 10, because of assignment in the setter
o.x; // evaluates to 11, because of addition in the getter
Here, we see that the functions also have access to the target object of the
assignment or lookup, via the this parameter. We could try to
encode this into our rules, but let's not get too far ahead of ourselves.
JavaScript objects have more subtleties up their sleeves. We can't forget
about prototype inheritance. Let's start with the same object o,
this time called parent, and use it as the prototype of another
object:
var parent = {
get x() { return this._x + 1; },
set x(v) { this._x = v * 2; }
};
var child = Object.create(parent);
child.x = 5; // Sets... what exactly to 10?
parent._x; // ???
child._x; // ???
parent.x; // ???
child.x; // ??? Take a minute to guess what you think each of the values should be. Click here to see the answers (which hopefully are what you expected).
So, JavaScript is passing the object in the lookup expression into the function, for both field access and field update. Something else subtle is going on, as well. Recall that before, when an update occurred on a field that wasn't present, JavaScript simply added it to the object. Now, on field update, we see that the assignment traverses the prototype chain to check for setters. This is fundamentally different from JavaScript before accessors―assignment never considered prototypes. So, our semantics needs to do two things:
- Pass the correct
thisargument to getters and setters; - Traverse the prototype chain for assignments.
Let's think about a simple way to pass the this argument to
getters:
(E-LookupGetter)
{ ⋯, str:[get:vg, set:vs], ⋯ }[strx] → vg({ ⋯, str:[get:vg, set:vs], ⋯ })
when strx = str
Here, we simply copy the object over into the first argument to the
function vg. We can (and do) desugar
functions to have an implicit first this argument to line up with
this invocation. But we need to think carefully about this rule's interaction
with prototype inheritance.
Here is E-Lookup-Proto from the original λJS:
(E-Lookup-Proto)
{ str1:v1, ⋯, "__proto__": vp, strn:vn, ⋯}[str] → vp[str]
when str ≠ str1, ⋯, strn, ⋯
Let's take a moment to look at this rule in conjunction with E-LookupGetter. If the field isn't found, and
__proto__ is present, it looks up the __proto__ field and performs the same
lookup on that object (we are eliding the case where proto is not present or
not an object for this presentation). But note something crucial: the
expression on the right hand side drops everything about the original
object except its prototype. If we applied this rule to child
above, the getter rule would pass parent to the getter instead of
child!
The solution is to keep track of the original object as we traverse the prototype chain. If we don't, the reduction relation simply won't have the information it needs to pass in to the getter or setter when it reaches the right point in the chain. This is a deep change―we need to modify our expressions to get it right:
p := [get: vg, set: vs] | [value: v]
v := str | { str1:p1, ⋯, strn:pn } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | ev[e] | ev[e=e] | e(e, ⋯) | ⋯
And now, when we do a prototype lookup, we can keep track of the same
this argument (written as vt)
the whole way up the chain, and the rules for getters and setters can use this
new piece of the expression:
(E-Lookup-Proto)
{ str1:v1, ⋯, "__proto__": vp, strn:vn, ⋯}vt[str] → vpvt[str]
when str ≠ str1, ⋯, strn, ⋯
(E-LookupGetter)
{ ⋯, str:[get:vg, set:vs], ⋯ }vt[strx] → vg(vt)
when strx = str
(E-UpdateSetter)
{ ⋯, str:[get:vg, set:vs], ⋯}vt[strx=v'] → vs(vt,v')
when strx = str
This idea was inspired by Di Gianantonio, Honsell, and Liquori's 1998 paper, A lambda calculus of objects with self-inflicted extension. They use a similar encoding to model method dispatches in a small prototype-based object calculus. The original expressions, e[e] and e[e=e], simply copy values into the new positions once the subexpressions have reduced to values:
(E-Lookup) v[str] → vv[str] (E-Update) v[str=v'] → vv[str=v']
The final set of evaluation rules and expressions is a little larger:
p := [get: vg, set: vs] | [value: v]
v := str | { str1:p1, ⋯, strn:pn } | func(x ⋯) . e | ⋯
e := e[e] | e[e=e] | ev[e] | ev[e=e] | e(e, ⋯) | ⋯
(E-Lookup)
v[str] → vv[str]
(E-Update)
v[str=v'] → vv[str=v']
(E-LookupGetter)
{ ⋯, str:[get:vg, set:vs], ⋯ }vt[strx] → vg(vt)
when strx = str
(E-Lookup-Proto)
{ str1:v1, ⋯, "__proto__": vp, strn:vn, ⋯}vt[str] → vpvt[str]
when str ≠ str1, ⋯, strn, ⋯
(E-UpdateSetter)
{ ⋯, str:[get:vg, set:vs], ⋯}vt[strx=v'] → vs(vt,v')
when strx = str
(E-Update-Proto)
{ str1:v1, ⋯, "__proto__": vp, strn:vn, ⋯}vt[str=v'] → vpvt[str=v']
when str ≠ str1, ⋯, strn, ⋯
This is most of the rules―we've elided some details to only present the
key insight behind the new ones. Our full semantics (discussed in our last post), handles the
details of the arguments object that is implicitly available
within getters and setters, and using built-ins, like
defineProperty, to add already-defined functions to existing
objects as getters and setters.
S5: A Semantics for Today's JavaScript
Tags: JavaScript, Semantics, Programming Languages
Posted on 11 November 2011.The JavaScript language isn't static―the ECMAScript committee is working hard to improve the language, and browsers are implementing features both in and outside the spec, making it difficult to understand just what "JavaScript" means at any point in time. Existing implementations aren't much help―their goal is to serve pages well and fast. We need a JavaScript architecture that can help us make sense of the upcoming (and existing!) features of the language.
To this end, we've developed S5, an ECMAScript 5 runtime, built on λJS, with the explicit goal of helping people understand and tinker with the language. We built it to understand the features in the new standard, building on our previous efforts for the older standard. We've now begun building analyses for this semantics, and are learning more about it as we do so. We're making it available with the hope that you can join us in playing with ES5, extending it with new features, and building tools for it.
S5 implements the core features of ES5 strict mode. How do we know this? We've tested S5 against Test262 to measure our progress. We are, of course, not feature complete, but we're happy with our progress, which you can check out here.
A Malleable Implementation
The semantics of S5 is designed to be two things: a language for writing down the algorithms of the specification, and a translation target for JavaScript programs. We've implemented an interpreter for S5, and a desugaring function that translates JavaScript source into S5 programs.
We have a number of choices to make in defining desugaring. The ECMAScript standard defines a whole host of auxiliary functions and library routines that we must model. Putting these implementations directly in the desugaring function would work, but would make desugaring unnecessary brittle, and require recompilation on every minor change. Instead, we implement the bulk of this functionality as an S5 program. The majority of our work happens in an environment file that defines the spec in S5 itself. The desugaring defines a translation from the syntactic forms of JavaScript to the (smaller) language of S5, filled with calls into the functions defined in this environment.
This separation of concerns is what makes our implementation so amenable to
exploration. If you want to try something out, you can edit the environment
file and rerun whatever tests you care to learn about. Want to try a different
implementation of the == operator? Just change the definition, as
it was pulled from the spec, at line
300. Want a more expressive Object.toString() that doesn't
just print "[object Object]"? That's right
here. No changing an interpreter, no recompiling a desugaring function
necessary.
The environment we've written reflects the standard's algorithms as we understand them in terms of S5. The desugaring from JavaScript to S5 code with calls into this library is informed by the specification's definitions of expression and statement evaluation. We have confidence in the combination of desugaring and library implementation, given our increasing test coverage. Further, we know how to continue―implement more of the spec and pass more test cases!
More than λJS
S5 is built on λJS, but extends it in three significant ways:
- Explicit getters and setters;
- Object fields with attributes, like
writableandconfigurable, built-in; - Support for
eval().
Attributes on objects weren't treated directly in the original
λJS.
In 5th Edition, they are crucial to several security-relevant operations on
objects. For example, the standard specifies Object.freeze(),
which makes an object's properties forever unwritable. S5 directly models the
writable and configurable attributes that make this
operation possible, and make its implementation in S5 easy to understand.
λJS explicitly elided eval() from its semantics. S5
implements eval() by performing desugaring within the
interpreter and then interpreting the desugared code. We implement only
the strict mode version of eval, which restricts the environment
that the eval'd code can affect. With these restrictions, we can
implement eval in a straightforward way within our interpreter.
We'll cover the details of how we do this, and why it works, in another post.
Building on S5
There's a ton we can do with S5. More, in fact, than we can do by ourselves:- Experiment with Harmony features: ECMAScript 6, or Harmony, as it is often called, is being designed right now. Proxies, string interpolation, syntactic sugar for classes, and modules are just a few of the upcoming features. Modeling them in S5 would help us understand these features better as they get integrated into the language.
- Build Verification Tools: Verification based on objects' attributes is an interesting research problem―what can we prove about interacting programs if we know about unwritable fields and inextensible objects? Building this knowledge into a type-checker or a program analysis could give interesting new guarantees.
- Abstract Our Machine: Matt Might and David van Horn wrote about abstracting λJS for program analysis. We've added new constructs to the language since then. Do they make abstraction any harder?
- Complete the Implementation: We've made a lot of progress, but there's still more ground to cover. We need support for more language features, like JSON and regular expressions, that would move our implementation along immensely. We'll work on this more, but anyone who wants to get involved is welcome to help.
If any of this sounds interesting, or if you're just curious, go ahead and check out S5! It's open source and lives in a Github repository. Let us know what you do with it!
The Essence of JavaScript
Tags: JavaScript, Semantics, Programming Languages
Posted on 29 September 2011.Back in 2008, the group decided to really understand JavaScript. Arjun had built a static analysis for JavaScript from scratch. Being the honest chap that he is, he was forced to put the following caveat into the paper:
"We would like to formally prove that our analysis is sound. A sound analysis would guarantee that our tool will never raise a false alarm, an imporant usability concern. However, a proof of soundness would require a formal semantics for JavaScript and the DOM in browsers, and this does not exist."
A "formal semantics for JavaScript [...] does not exist"? Didn't he know
about the official documents on such matters, the ECMAScript standard?
ECMAScript 3rd edition, the standard at the time, was around 180 pages long,
written in prose and pseudocode. Reading it didn't help much. It includes
gems such as this description of the switch statement:
1. Let A be the list of CaseClause items in the first
CaseClauses, in source text order.
2. For the next CaseClause in A, evaluate CaseClause. If there is
no such CaseClause, go to step 7.
3. If input is not equal to Result(2), as defined by the !==
operator, go to step 2.
4. Evaluate the StatementList of this CaseClause.
5. If Result(4) is an abrupt completion then return Result(4).
6. Go to step 13.
7. Let B be the list of CaseClause items in the second
CaseClauses, in source text order.
8. For the next CaseClause in B, evaluate CaseClause. If there is
no such CaseClause, go to step 15.
9. If input is not equal to Result(8), as defined by the !==
operator, go to step 8.
10. Evaluate the StatementList of this CaseClause.
11. If Result(10) is an abrupt completion then return Result(10).
12. Go to step 18.
...
And this is just one of 180 pages of lesser or greater eloquence. With this as his formal reference, it's no wonder Arjun had a hard time making soundness claims.
Around the same time, Ankur Taly, Sergio Maffeis, and John Mitchell noticed the same problem. They presented a formal semantics for JavaScript in their APLAS 2008 paper. You can find their semantics here, and it is a truly staggering effort, running for 40+ pages (that's at least four times easier to understand!). However, we weren't quite satisfied. Their semantics formalizes the ECMAScript specification as written, and therefore inherits some of its weirdness, such as heap-allocated "scope objects", implicit coercions, etc. We still couldn't build tools over it, and were unwilling to do 40-page case analyses for proofs. Leo Meyerovich, peon extraordinaire and friend of the blog, felt the same:
"Challenging current attempts to analyze JavaScript, there is no formal semantics realistic enough to include many of the attack vectors we have discussed yet structured and tractable enough that anyone who is not the inventor has been able to use; formal proofs are therefore beyond the scope of this work."
How To Tackle JavaScript: The PLT Way
We decided to start smaller. In the fall of 2009, Arjun wrote down a semantics for the "core" of JavaScript that fits on just three pages (that's 60 times easier to understand!). This is great programming languages research—we defined away the hairy parts of the problem and focused on a small core that was amenable to proof. For these proofs, we could assume the existence of a trivial desugaring that maps real JavaScript programs into programs in the core semantics, which Arjun dubbed λJS.
Things were looking great until one night Arjun had a few too many glasses of wine and decided to implement desugaring. Along with Claudiu Saftoiu, he wrote a thousand lines of Haskell that turns JavaScript programs into λJS programs. Even worse, they implemented an interpreter for λJS, so the resulting programs actually run. They had therefore produced a JavaScript runtime.
Believe it or not, there are other groups in the business of creating JavaScript runtimes, namely Google, Mozilla, Microsoft, and a few more. And since they care about the correctness of their implementations, they have actual test suites. Which Arjun's system could run, and give answers for, that may or may not be the right ones:
As it turns out, Arjun and Claudiu did a pretty good job. λJS agrees with Mozilla SpiderMonkey on a few thousand lines of tests. We say "agreed" and not "passed" because SpiderMonkey fails some of its own tests. Without any other standard of correctness, λJS strives for bug-compatibility with SpiderMonkey on those tests.
Building on λJS
λJS is discussed in our ECOOP paper, but it's the work built on λJS that's most interesting. We've built the following systems ourselves:
- A type-checker for JavaScript that employs a novel mix of type-checking and flow analysis ("flow typing"), discussed in our ESOP 2011 paper, and
- An extension to the above type-checker to verify ADsafe, as discussed in our USENIX Security 2011 paper.
- David van Horn and Matt Might use λJS to build an analytic framework for JavaScript,
- Rodolfo Toledo and Éric Tanter use λJS to specify aspects for JavaScript,
- IBEX, from Microsoft Research, uses λJS for its JavaScript backend to produce verified Web browser extensions, and
- Others have a secret reimplementation of λJS in Java. We are now enterprise-ready.
Want to use λJS to write JavaScript tools? Check out our software and let us know what you think!
Coming up next: The latest version of JavaScript, ECMAScript 5th ed.,
is vastly improved. We've nearly finished updating our JavaScript semantics to
match ECMAScript 5th ed. Our new semantics uses the official ECMAScript test
suite and tackles problems, such as eval, that the original
λJS elided. We'll talk about it next time. Update:
We've written about our update, dubbed S5, its semantics for accessors,
and a particularly interesting
example.
ADsafety
Tags: Browsers, JavaScript, Programming Languages, Security, Types, Verification
Posted on 13 September 2011.
A mashup is a webpage that mixes and mashes content from various sources. Facebook apps, Google gadgets, and various websites with embedded maps are obvious examples of mashups. However, there is an even more pervasive use case of mashups on the Web. Any webpage that displays third-party ads is a mashup. It's well known that third-party content can include third-party cookies; your browser can even block these if you're concerned about "tracking cookies". However, third party content can also include third-party JavaScript that can do all sorts of wonderful and malicious things (just some examples).
Is it possible to safely embed untrusted JavaScript on a page? Google Caja, Microsoft Web Sandbox, and ADsafe are language-based Web sandboxes that try to do so. Language-based sandboxing is a programming language technique that restricts untrusted code using static and runtime checks and rewriting potential dangerous calls to safe, trusted functions.
Sandboxing JavaScript, with all its corner cases, is particularly hard. A
single bug can easily break the entire sandboxing system. JavaScript sandboxes
do not clearly state their intended guarantees, nor do they clearly argue why
they are safe. 
Verifying Web Sandboxes
A year ago, we embarked on a project to verify ADsafe, Douglas Crockford's Web sandbox. ADsafe is admittedly the simplest of the aforementioned sandboxes. But, we were also after the shrimp bounty that Doug offers for sandbox-breaking bugs:
Write a program [...] that calls the alert function when run on any browser. If the program produces no errors when linted with the ADsafe option, then I will buy you a plate of shrimp. (link)A year later, we've produced a USENIX Security paper on our work, which we presented in San Francisco in August. The paper discusses the many common techniques employed by Web sandboxes and discusses the intricacies of their implementations. (TLDR: JavaScript and the DOM are really hard.) Focusing on ADsafe, it precisely states what ADsafety actually means. The meat of the paper is our approach to verifying ADsafe using types. Our verification leverages our earlier work on semantics and types for JavaScript, and also introduces some new techniques:
- Check out the ★s and ☠s in our object types; we use them to type-check "scripty" features of JavaScript. ☠ marks a field as "banned" and ★ specifies the type of all other fields.
- We also characterize JSLint as a type-checker. The Widget type presented in the paper specifies, in 20 lines, the syntactic restrictions of JSLint's ADsafety checks.
Unlike conventional type systems, ours does not prevent runtime errors. After all, stuck programs are safe because they trivially don't execute any code. If you think type systems only catch "method not found" errors, you should have a look at ours.
We found bugs in both ADsafe and JSLint that manifested as type errors. We reported all of them and they were promptly fixed by Doug Crockford. A big thank you to Doug for his encouragement, for answering our many questions, and for buying us every type of shrimp dish in the house.

Learn more about ADsafety! Check out:
- The paper, code, and proofs;
- Video of Arjun presenting at USENIX Security;
- ADsafe and JSLint.
